Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations

Zhauyt, Algazy; Musayev, Janat; Bazanova, Inna; Mustapaev, Koldasbay

doi:10.21595/vp.2025.25010

Vibroengineering Procedia

Browse Procedia

Published: 15 May 2025

Check for updates

Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations

Algazy Zhauyt¹

Janat Musayev²

Inna Bazanova³

Koldasbay Mustapaev⁴

¹Department of Electronic Engineering, Almaty University of Power Engineering and Telecommunications named after G. Daukeyev, Almaty, 050013, Kazakhstan

^{2, 4}Department of Rolling Stock, Mukhametzhan Tynyshpayev ALT University, Almaty, 050012, Kazakhstan

³Department of Higher School of Marketing and Logistics, Turan University, Almaty, 050020, Kazakhstan

Corresponding Author:

Algazy Zhauyt

Cite the article Download PDF

Downloads 201

Abstract

The double pendulum is a well-known system exhibiting nonlinear dynamics and chaotic behavior. This study extends the conventional rigid double pendulum by introducing elastic extensions in the links, leading to a system known as the elastic double pendulum. The mathematical model incorporates both rotational and translational motion, accounting for elastic deformations using Hooke’s Law. The governing equations are derived using Lagrangian mechanics, considering both gravitational and spring potential energy contributions. Numerical simulations are performed to compare the motion of the elastic and rigid double pendulums, highlighting differences in phase-space trajectories, energy transfer, and stability characteristics. Results demonstrate that elasticity introduces additional oscillatory components, increases system nonlinearity, and affects the overall predictability of motion. These findings provide insights into elastic multi-body dynamics and have potential applications in flexible robotic arms, soft mechanisms, and bio-inspired locomotion.

Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations

Highlights

Elastic and rigid double pendulum
Highlighting differences in phase-space trajectories
Elastic multi-body dynamics
The classical double pendulum
Advances in nonlinear dynamics and chaos theory

1. Introduction

The classical double pendulum, composed of two rigid links connected by revolute joints, is widely studied for its rich dynamic behavior and sensitivity to initial conditions. Despite its simplicity, it serves as a prototypical example of chaos in mechanical systems. However, in real-world applications such as flexible robotics, biomechanics, and aerospace structures, components often exhibit elastic behavior. Therefore, modeling these systems using rigid-body dynamics alone is inadequate. Recent work has extended the theoretical understanding of the double pendulum through analytical studies of low-energy normal modes [1], near-resonance behaviors [2], and distributed mass configurations [3]. At the same time, advances in nonlinear dynamics and chaos theory [4-6] have clarified the role of sensitivity, fractal basin boundaries, and global attractor structures. This study builds on these developments by extending the rigid double pendulum with linkwise elasticity, leading to a hybrid dynamic model. Incorporating elastic extensions alters both the kinetic and potential energy formulations, resulting in a coupled system of nonlinear differential equations involving both angular and linear degrees of freedom [4]. The objective of this work is to derive the governing equations of motion for the elastic double pendulum using Lagrangian mechanics and to numerically analyze its behavior in comparison with the conventional rigid model. By simulating both systems under identical initial conditions, we aim to highlight the role of elastic energy storage, oscillation amplitudes, phase-space structures, and sensitivity to initial conditions. The comparative analysis not only enhances understanding of elastic multibody systems but also provides insights applicable to the design and control of flexible robotic and biomechanical structures. The classical double pendulum [5], composed of two rigid links connected by revolute joints, is widely studied for its rich dynamic behavior and sensitivity to initial conditions.

2. Materials and methods

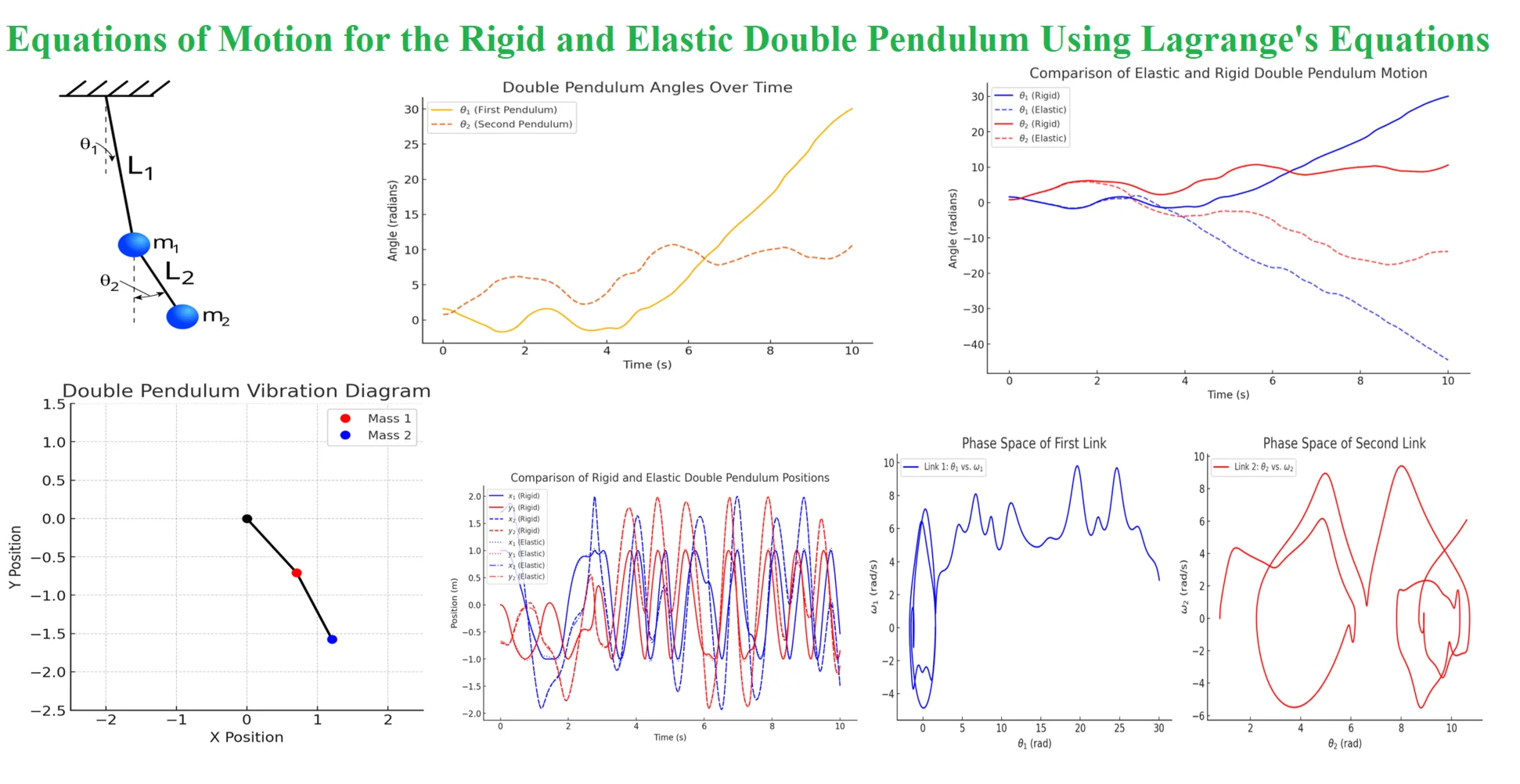
The double pendulum (see Fig. 1) consists of two rigid links connected serially and free to swing in a vertical plane. Its motion is fully described by two generalized coordinates. Position equations:

1

x_{1} = L_{1} s i n θ_{1},

2

y_{1} = {- L}_{1} c o s θ_{1},

3

x_{2} = L_{1} s i n θ_{1} + L_{2} s i n θ_{2},

4

y_{2} = {- L}_{1} c o s θ_{1} - L_{2} c o s θ_{2} .

Velocity equations (first derivative of position):

5

\frac{d x_{1}}{d t} = L_{1} c o s θ_{1} \frac{d θ_{1}}{d t},

6

\frac{d y_{1}}{d t} = {- L}_{1} s i n θ_{1} \frac{d θ_{1}}{d t},

7

\frac{d x_{2}}{d t} = L_{1} c o s θ_{1} \frac{d θ_{1}}{d t} + L_{2} c o s θ_{2} \frac{d θ_{2}}{d t},

8

\frac{d y_{2}}{d t} = - L_{1} s i n θ_{1} \frac{d θ_{1}}{d t} - L_{2} s i n θ_{2} \frac{d θ_{2}}{d t} .

Potential energy $U$ . Potential energy is given by:

9

U = m_{1} g y_{1} + m_{2} g y_{2} .

Substituting:

10

U = m_{1} g (- L_{1} c o s θ_{1}) + m_{2} g (- L_{1} c o s θ_{1} - L_{2} c o s θ_{2}),

U = - (m_{1} + m_{2}) g L_{1} c o s θ_{1} - m_{2} g L_{2} c o s θ_{2} .

Kinetic energy $T$ . Kinetic energy is given by:

11

T = \frac{1}{2} m_{1} ϑ_{1}^{2} + \frac{1}{2} m_{2} ϑ_{2}^{2},

12

ϑ_{1}^{2} = {(\frac{d x_{1}}{d t})}^{2} + {(\frac{d y_{1}}{d t})}^{2} = {(L_{1} c o s θ_{1} \dot{θ_{1}})}^{2} + {({- L}_{1} s i n θ_{1} \dot{θ_{1}})}^{2} = L_{1}^{2} {\dot{θ}}_{1}^{2},

13

ϑ_{2}^{2} = {(\frac{d x_{2}}{d t})}^{2} + {(\frac{d y_{2}}{d t})}^{2} = {(L_{1} c o s θ_{1} {\dot{θ}}_{1} + L_{2} c o s θ_{2} \dot{θ_{2}})}^{2} + {({- L}_{1} s i n θ_{1} \dot{θ_{1}} - L_{2} s i n θ_{2} \dot{θ_{2}})}^{2} .

Expanding $ϑ_{2}^{2}$ :

14

ϑ_{2}^{2} = (L_{1}^{2} {\dot{θ}}_{1}^{2} + L_{2}^{2} {\dot{θ}}_{2}^{2} + 2 L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2}) .

Final kinetic energy expression:

15

T = \frac{1}{2} m_{1} L_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} (L_{1}^{2} {\dot{θ}}_{1}^{2} + L_{2}^{2} {\dot{θ}}_{2}^{2} + 2 L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2}) .

Fig. 1Scheme of the double pendulum

Rearranging:

16

T = \frac{1}{2} (m_{1} + m_{2}) L_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} L_{2}^{2} {\dot{θ}}_{2}^{2} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} .

Lagrangian $L = T - U$ :

17

T = \frac{1}{2} (m_{1} + m_{2}) L_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} L_{2}^{2} {\dot{θ}}_{2}^{2} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} + (m_{1} + m_{2}) g L_{1} c o s θ_{1} - m_{2} g L_{2} c o s θ_{2} .

Compute $\frac{\partial L}{\partial {\dot{θ}}_{1}}$ and $\frac{\partial L}{\partial {\dot{θ}}_{2}}$ :

18

\frac{\partial L}{\partial {\dot{θ}}_{1}} = (m_{1} + m_{2}) L_{1}^{2} {\dot{θ}}_{1} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1},

19

\frac{\partial L}{\partial {\dot{θ}}_{2}} = m_{2} L_{2}^{2} {\dot{θ}}_{2} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\dot{θ}}_{1} .

Compute $\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{1}})$ and $\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{2}})$ :

20

\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{1}}) = (m_{1} + m_{2}) L_{1}^{2} {\ddot{θ}}_{1} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\ddot{θ}}_{2} - m_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2},

21

\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{2}}) = m_{2} L_{2}^{2} {\ddot{θ}}_{2} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\ddot{θ}}_{1} + m_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} .

Compute $\frac{\partial L}{\partial θ_{1}}$ and $\frac{\partial L}{\partial θ_{2}}$ :

22

\frac{\partial L}{\partial θ_{1}} = {- m}_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} - (m_{1} + m_{2}) g L_{1} c o s θ_{1},

23

\frac{\partial L}{\partial θ_{2}} = m_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} - m_{2} g L_{2} s i n θ_{2} .

Euler-Lagrange equations:

24

\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{i}}) - \frac{\partial L}{\partial θ_{i}} = Q_{i} .

Assuming no external torques $Q_{1} = Q_{2} = 0$ , we obtain the equations of motion:

25

(m_{1} + m_{2}) L_{1}^{2} {\ddot{θ}}_{1} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\ddot{θ}}_{2} - m_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} + (m_{1} + m_{2}) g L_{1} s i n θ_{1} = 0,

26

m_{2} L_{2}^{2} {\ddot{θ}}_{2} + m_{2} L_{1} L_{2} c o s (θ_{1} - θ_{2}) {\ddot{θ}}_{1} + m_{2} L_{1} L_{2} s i n (θ_{1} - θ_{2}) {\dot{θ}}_{1} {\dot{θ}}_{2} + m_{2} g L_{2} s i n θ_{2} = 0 .

These are the equations of motion for the double pendulum in terms of $θ_{1}$ and $θ_{2}$ .

3. Results

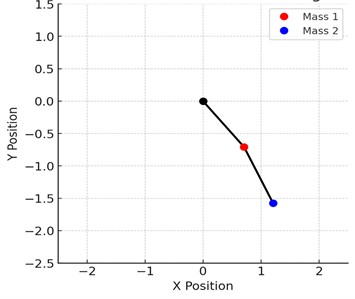
The numerical simulation of both the rigid and elastic double pendulum [1] systems reveals notable differences in their dynamic behavior. In the rigid case, the motion of the pendulum arms exhibits periodic and chaotic transitions typical of nonlinear systems. In contrast, the elastic double pendulum [2] demonstrates more complex and irregular motion due to the coupling between angular and elastic (spring) degrees of freedom (see Fig. 2). Time-dependent plots of angles $θ_{1}$ and $θ_{2}$ (in Fig. 3), as well as Cartesian positions $x_{1}$ , $y_{1}$ , $x_{2}$ , $y_{2}$ show larger oscillations and modulated amplitudes in the elastic system. These results confirm that elasticity introduces additional dynamic modes, increases sensitivity to initial conditions, and enhances the overall complexity of the system’s motion.

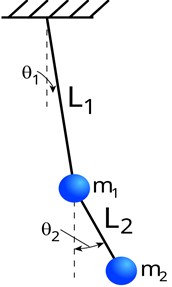
Fig. 2Diagram of the double pendulum in vibration. The black lines represent the pendulum arms, while the red and blue circles indicate the positions of the two masses

Diagram of the double pendulum in vibration. The black lines represent the pendulum arms, while the red and blue circles indicate the positions of the two masses

The elastic double pendulum in Fig. 4 exhibits oscillatory behavior due to spring elongation and contraction. The rigid double pendulum [3] follows a smoother trajectory without additional oscillations. The second link $θ_{2}$ in the elastic system shows more deviation compared to the rigid system, indicating energy transfer from spring oscillations.

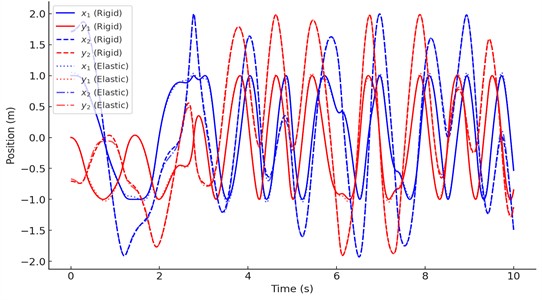
The elastic pendulum [4] in Fig. 5 exhibits additional oscillations due to the spring extensions, making its motion more complex. The rigid pendulum follows a smoother path, with predictable periodic motion. The elastic system has larger deviations in $x_{2}$ , $y_{2}$ , indicating greater nonlinearity and energy transfer between rotational and elastic modes.

The first link (blue) has a more structured and constrained motion. The second link (red) exhibits a more chaotic trajectory, indicating more irregular behavior (in Fig. 6). The second link’s motion is more sensitive to initial conditions and energy changes.

Fig. 3Plot of θ1 and θ2 over time for the double pendulum. The solid line represents the angle of the first pendulum, while the dashed line represents the angle of the second pendulum

Plot of θ1 and θ2 over time for the double pendulum. The solid line represents the angle of the first pendulum, while the dashed line represents the angle of the second pendulum

Fig. 4Comparison of the motion of θ1 and θ2 for the rigid double pendulum and the elastic double pendulum: solid blue θ1 (rigid); dashed blue θ1 (elastic); solid red θ2 (rigid); dashed red θ2 (elastic)

Comparison of the motion of θ1 and θ2 for the rigid double pendulum and the elastic double pendulum: solid blue θ1 (rigid); dashed blue θ1 (elastic); solid red θ2 (rigid); dashed red θ2 (elastic)

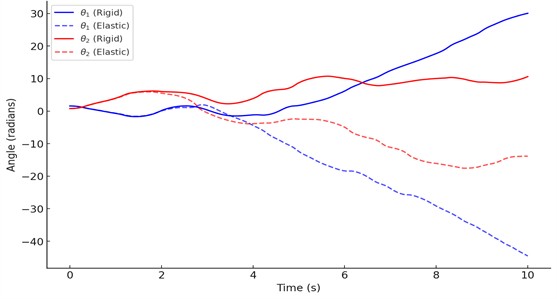
Fig. 5Comparison of the positions x1, y1, x2, y2 for the rigid and elastic double pendulums over time: solid blue x1 (rigid); solid red y1 (rigid); dashed blue x2 (rigid); dashed red y2 (rigid); dotted blue x1 (elastic); dotted red y1 (elastic); dash-dot blue x2 (elastic); dash-dot red y2 (elastic)

Comparison of the positions x1, y1, x2, y2 for the rigid and elastic double pendulums over time: solid blue x1 (rigid); solid red y1 (rigid); dashed blue x2 (rigid); dashed red y2 (rigid); dotted blue x1 (elastic); dotted red y1 (elastic); dash-dot blue x2 (elastic); dash-dot red y2 (elastic)

4. Discussion

The inclusion of elasticity fundamentally alters the dynamic behavior of the double pendulum [5, 6]. Energy is stored and released through spring deformation, leading to modulated angular motion and coupling between longitudinal and rotational dynamics. These findings are relevant in the design of compliant robotic arms, soft manipulators, and bio-inspired mechanisms. The model also demonstrates sensitivity to spring stiffness and initial conditions, highlighting the importance of precise parameter control in engineering systems.

Fig. 6Phase-space comparison of the motion of the two links in the double pendulum: a) the phase space (θ1 vs ω1) for the first link; b) the phase space (θ2 vs ω2) for the second link

Phase-space comparison of the motion of the two links in the double pendulum: a) the phase space (θ1 vs ω1) for the first link; b) the phase space (θ2 vs ω2) for the second link

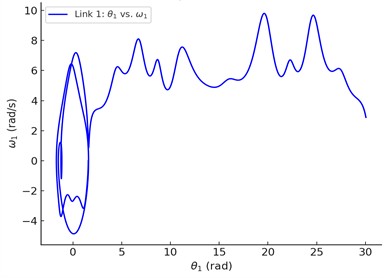
a)

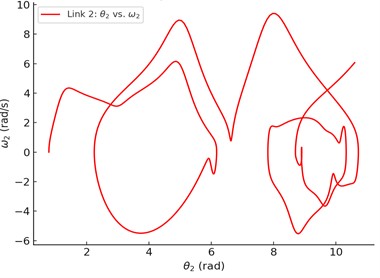
b)

5. Conclusions

This study presents a comprehensive comparison between rigid and elastic double pendulum systems. By introducing longitudinal elasticity along each link, the system exhibits coupled rotational and vibrational dynamics, leading to enriched and more complex behavior. While not necessarily chaotic under all initial conditions, this configuration allows for dynamic regimes that go beyond those observed in the rigid double pendulum. The modeling and simulation framework provides a useful tool for exploring elastic multibody systems, with potential applications in robotics, biomechanics, and aerospace. Future work could include damping effects, three-dimensional extensions, and control strategies for trajectory stabilization.

References

I. Kovacic, M. Zukovic, and D. Radomirovic, “Normal modes of a double pendulum at low energy levels,” Nonlinear Dynamics, Vol. 99, No. 3, pp. 1893–1908, Jan. 2020, https://doi.org/10.1007/s11071-019-05424-5

Publisher
T. S. Amer, R. Starosta, A. S. Elameer, and M. A. Bek, “Analyzing the stability for the motion of an unstretched double pendulum near resonance,” Applied Sciences, Vol. 11, No. 20, p. 9520, Oct. 2021, https://doi.org/10.3390/app11209520

Publisher
M. Z. Rafat, M. S. Wheatland, and T. R. Bedding, “Dynamics of a double pendulum with distributed mass,” American Journal of Physics, Vol. 77, No. 3, pp. 216–223, Mar. 2009, https://doi.org/10.1119/1.3052072

Publisher
T. Stachowiak and T. Okada, “A numerical analysis of chaos in the double pendulum,” Chaos, Solitons and Fractals, Vol. 29, No. 2, pp. 417–422, Jul. 2006, https://doi.org/10.1016/j.chaos.2005.08.032

Publisher
B. Qin and Y. Zhang, “A novel global perspective: Characterizing the fractal basins of attraction and the level of chaos in a double pendulum,” Chaos, Solitons and Fractals, Vol. 189, No. 2, p. 115694, Dec. 2024, https://doi.org/10.1016/j.chaos.2024.115694

Publisher
T. Shinbrot, C. Grebogi, J. Wisdom, and J. A. Yorke, “Chaos in a double pendulum,” American Journal of Physics, Vol. 60, No. 6, pp. 491–499, Jun. 1992, https://doi.org/10.1119/1.16860

Publisher

About this article

Received

07 April 2025

Accepted

23 April 2025

Published

15 May 2025

SUBJECTS

Chaos, nonlinear dynamics and applications

DOI

https://doi.org/10.21595/vp.2025.25010

Keywords

double pendulum

elastic

rigid

nonlinear dynamics

Lagrange’s equations

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 11 18

On the issue of the motion of balls in a double pendulum

Guntis Strautmanis, Igors Schukin, Gennadiy Filimonikhin, Mareks Mezitis, Kristine Carjova

Research article

2021 05 06

Effect of excitation frequency on nonlinear vibration of crack fault in multi-stage gear transmission system

Hongwei Zhang, Xin Wang, Qiaorong Zhao, Taotao Li

Research article

2019 10 19

The control strength quantification analysis of outer pendulum rod for double inverted pendulum

Wencong Fu, Chan Wang, Peng Xu, Yuanhong Dan

Research article

2018 05 22

Calculation of mechanism motion using discrete time approach

Lubor Zháňal, Petr Porteš

A. Zhauyt, J. Musayev, I. Bazanova, and K. Mustapaev, “Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations,” Vibroengineering Procedia, Vol. 58, pp. 154–160, May 2025, https://doi.org/10.21595/vp.2025.25010

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25010
UR  - https://doi.org/10.21595/vp.2025.25010
TI  - Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations
T2  - Vibroengineering Procedia
AU  - Zhauyt, Algazy
AU  - Musayev, Janat
AU  - Bazanova, Inna
AU  - Mustapaev, Koldasbay
PY  - 2025
DA  - 2025/05/15
PB  - Extrica
SP  - 154-160
VL  - 58
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Zhauyt_2025, title={Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations}, volume={58}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25010}, DOI={10.21595/vp.2025.25010}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Zhauyt, Algazy and Musayev, Janat and Bazanova, Inna and Mustapaev, Koldasbay}, year={2025}, month=may, pages={154–160} }

Copy Bibtex

Copied to clipboard!

[1]A. Zhauyt, J. Musayev, I. Bazanova, and K. Mustapaev, “Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations,” Vibroengineering Procedia, vol. 58, pp. 154–160, May 2025, doi: 10.21595/vp.2025.25010.

Copy IEEE

Copied to clipboard!

Zhauyt, Algazy, Janat Musayev, Inna Bazanova, and Koldasbay Mustapaev. “Equations of Motion for the Rigid and Elastic Double Pendulum Using Lagrange’s Equations.” Vibroengineering Procedia 58 (May 15, 2025): 154–60. https://doi.org/10.21595/vp.2025.25010.

Copy Chicago

Copied to clipboard!

Equations of motion for the rigid and elastic double pendulum using Lagrange’s equations

Abstract

Highlights

1. Introduction

2. Materials and methods

3. Results

4. Discussion

5. Conclusions

References

About this article

Related Articles