Abstract
Sparse reconstruction algorithm is one of the main research topics in compressed sensing. To address the shortcomings of existing iteratively reweighted -norm minimization methods, which exhibit poor performance in low-frequency sound source identification and weak anti-interference capability, this paper proposes an improved iteratively reweighted -norm minimization method. Unlike traditional methods, this method introduces a log-sum penalty function and constructs a surrogate function, transforming the problem into an effective form for solving the source strength distribution vector. Through numerical simulations comparing the two methods under different frequencies and signal-to-noise ratios (SNR), the results demonstrate that the proposed method enhances both the sound source identification accuracy and anti-interference capability of the algorithm, while also being able to adapt to lower frequency ranges.
1. Introduction
Compressed Sensing Theory [1]-[3] has attracted widespread attention from scholars due to its ability to achieve high-precision signal reconstruction with lower sampling rates, significantly reducing the required number of sensors and measurement data volume.
Current compressed sensing reconstruction methods primarily fall into three categories: convex optimization algorithms [4]-[6], which leverage the equivalence between the -norm and -norm under the Restricted Isometry Property (RIP) condition of the measurement matrix, transforming the intractable -norm minimization problem into a solvable -norm minimization problem addressed through mature convex optimization techniques; greedy algorithms [7]-[9], which iteratively select atoms based on signal-atom correlations to gradually form a support set for signal vector approximation; and Bayesian sparse reconstruction algorithms [10]-[12], which reformulate signal reconstruction as a Bayesian inference problem by assuming signal prior distributions. Among these, convex optimization algorithms can obtain globally optimal solutions, with -norm minimization emerging as one of the most widely used models due to its computational efficiency and sparsity guarantees. However, standard -norm minimization faces limitations, such as inaccuracies in estimating non-Gaussian sparse coefficients. To address this, iteratively reweighted algorithms have gained prominence for their effectiveness in enhancing reconstruction accuracy.
To improve low-frequency sound source identification accuracy and anti-interference capability, this study proposes an enhanced algorithm based on iteratively reweighted -norm minimization. By introducing a log-sum penalty function into the -norm minimization framework and constructing a surrogate function to derive weighting matrices, the method transforms the problem into a tractable form for solving source strength distribution vectors, thereby achieving sparse solutions.
2. Fundamental theory
2.1. Compressed sensing reconstruction algorithm
The fundamental concept of compressed sensing theory involves three sequential operations: first representing the original signal as a sparse signal compatible with compressed sensing processing, then performing compressive sampling on the sparse signal using a measurement matrix to acquire measurement data and ultimately recovering the sparse signal from these measurements through reconstruction algorithms. In the context of sound source identification applications, the critical implementation challenge resides in constructing an appropriate sensing matrix, where successful acquisition of this matrix determines the effectiveness of spatial sound field reconstruction and direction-of-arrival estimation.
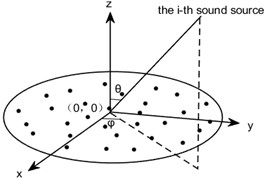
A planar microphone array measurement model is initially established as shown in Fig. 1, comprising microphones (denoted by ●). With the array center as the origin, a Cartesian coordinate system is constructed where the Direction of Arrival (DOA) of sound sources is characterized by coordinates (, ). Here, represents the elevation angle between the incident direction of the -th sound source and the -axis, while denotes the azimuth angle between the -axis and the projection of the -th source’s incident direction onto the - plane, with angular constraints defined as 0° 90° and 0° 360°.
Fig. 1Planar array sampling acoustic signal model
Assuming the target sound source region is discretized into fixed grid points, the -dimensional vector formed by the microphone-received signals can be expressed as:
where, is the sensing matrix; represents the source strength distribution vector.
Let and represent the -dimensional vectors composed of the -axis and -axis coordinates of all microphones, respectively. The sensing matrix () can be expressed as:
where, , ; , is the wavelength.
In practice, when , Eq (1) becomes an underdetermined system of linear equations, for which no analytical solution exists. However, if the vector possesses sparsity, it can be accurately recovered by solving the following -norm minimization problem:
where represents the tolerance for the noise signal (). Although Eq. (3) is an NP-hard problem and generally difficult to solve, it is equivalent to the following -norm minimization problem:
For Eq. (4), it can be solved using the convex optimization toolkit CVX to obtain the source strength corresponding to each fixed grid point, thereby enabling sound source DOA (Direction of Arrival) estimation and source strength quantification.
2.2. Improved iteratively reweighted L1 minimization method
The output results obtained by directly solving Eq. (4) often exhibit certain deviations. IRL1 further reduces these deviations by performing iterative optimization of the sound source distribution based on the L1-norm minimization solution. This method first employs a logarithmic sum penalty function that promotes sparsity more effectively than the norm, specifically , to construct the objective function, leading to the following optimization problem:
where, is a positive parameter that serves a dual role: on one hand, it ensures the logarithmic function is properly defined, and on the other hand, it acts as a control parameter for the iterative process. By initializing to a small value (e.g., 1) and gradually reducing it to zero during iterations, it guarantees that the global optimal solution of Eq. (5) converges to a neighborhood near the true solution.
Let denote the source strength distribution vector obtained after the -th iteration. In the -th iteration, construct a surrogate function for , satisfying , where equality holds if and only if . Here:
By removing the constant term in Eq. (6), we obtain:
Correspondingly, Eq. (5) is reformulated into the following surrogate function form:
Let the weighted matrix , where the -th weight coefficient is expressed as follows:
Therefore, the problem is transformed into solving the following equation:
Utilize the CVX toolbox to iteratively solve Eq. (10) for sound source DOA estimation.
Compared to the traditional iteratively reweighted -norm minimization algorithm, the proposed algorithm introduces a log-sum penalty function with enhanced sparsity-promoting capability, and simplifies the problem into a form that efficiently solves for the source strength distribution vector by constructing a surrogate function.
3. Numerical simulation
3.1. Performance analysis of various algorithms at different frequencies
The numerical simulation encompassed two distinct scenarios: a single sound source and dual coherent sound sources. In the single-source configuration, a point source was positioned at (18°, 72°), while the dual-source scenario involved two equal-intensity coherent point sources located at (54°, 72°) and (54°, 126°) respectively. The measurement array, designed in accordance with compressed sensing theory, adopted a sector-wheel topology comprising 18 microphones strategically distributed across nodal positions within a 0.4 m×0.4 m rectangular region. This array maintained parallelism with the focal plane at a standoff distance of 0.5 m. The focal plane itself was discretized into a 6×21 grid of reconstruction points. To enhance practical relevance, Gaussian white noise was introduced into the acoustic pressure measurements, achieving a SNR of 30 dB through controlled additive noise implementation.
Fig. 2 presents the sound source identification results of the conventional IRL1 algorithm and the enhanced IRL1 method at a source frequency of 1000 Hz. In the figure, “○” denotes actual source positions, while “*” represents identified source locations.
Fig. 2Source localization performance at a sound source frequency of 1000 Hz
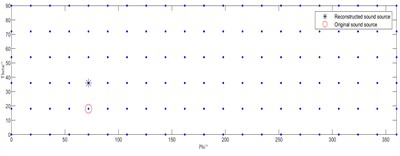
a) IRL1
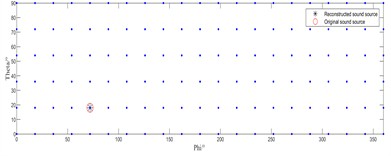
b) Improved IRL1
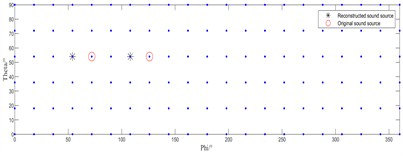
c) IRL1
d) Improved IRL1
As shown in Fig. 2 for the 1000 Hz acoustic source frequency, the conventional IRL1 algorithm in Fig. 2(a) and 2(c) yields completely erroneous identification results. In contrast, under both single-source (Fig. 2(b)) and dual-source (Fig. 2(d)) conditions, our enhanced IRL1 algorithm successfully localizes all acoustic sources with positional accuracy.
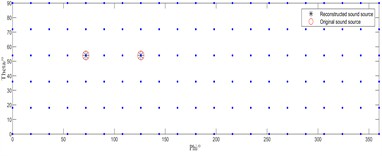
When the source frequency increases to 1500 Hz, Fig. 3(a) and Fig. 3(c) reveal that while the conventional IRL1 algorithm shows improved localization performance compared to lower frequencies, it still fails to correctly identify the single-source position. In dual-source scenarios, it accurately locates the right-side source but exhibits significant positional error for the left-side source. Conversely, our enhanced IRL1 algorithm (Fig. 3(b) and 3(d)) demonstrates robust performance by accurately identifying all true source positions under both test conditions.
Fig. 3Source localization performance at a sound source frequency of 1500 Hz
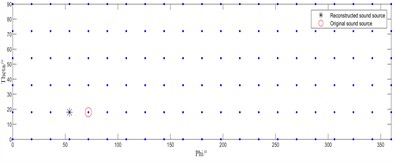
a) IRL1
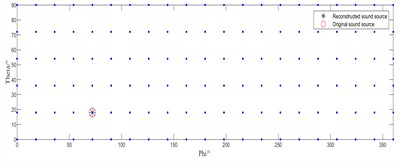
b) Improved IRL1
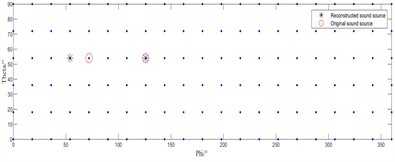
c) IRL1
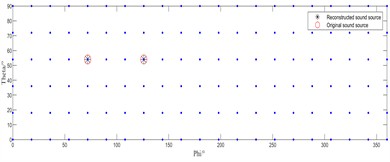
d) Improved IRL1
3.2. Performance analysis of algorithms under low SNR condition
Maintaining the original simulation conditions, simulation tests were conducted with the frequency set to 2000 Hz and SNR at 5 dB.
From Fig. 4(a), it can be observed that the conventional IRL1 algorithm accurately identifies the left-side acoustic source but still exhibits significant positional error in localizing the right-side source. In Fig. 4(b), the enhanced IRL1 algorithm proposed in this study achieves precise localization of both acoustic sources at their true positions.
Fig. 4Source localization effect diagram of two algorithms at a SNR of 5 dB
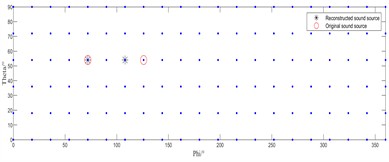
a) IRL1
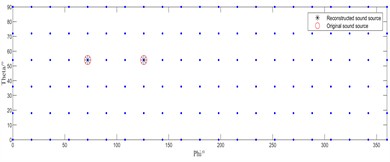
b) Improved IRL1
4. Experimental validation
To validate the correctness and effectiveness of the proposed method, experiments were conducted using a 30-microphone array from HBK for loudspeaker sound source identification. Fig. 5 illustrates the experimental setup. The loudspeaker’s DOA was set to (18°, 72°), corresponding to coordinates (0.0502, 0.1545, 0.500) m, with a sampling frequency of 16,348 Hz. The sound pressure information of the sound sources was measured, and repetitive verification was conducted on the MATLAB platform. The identification results of the IRL1 algorithm and its improved version at 1000Hz, as shown in Fig. 6, were ultimately obtained.
As can be seen from the experimental results, under low-frequency conditions, the traditional IRL1 algorithm fails to accurately identify the sound source. However, the improved IRL1 algorithm proposed in this paper can still accurately identify the location of the real sound source, significantly improving the performance of identifying low-frequency sound sources.
Fig. 5Experimental setup diagram

Fig. 6Experimental recognition results diagram
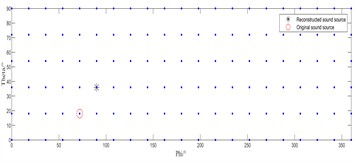
a) IRL1
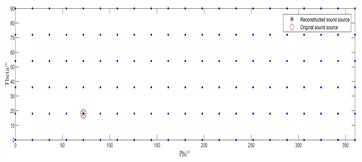
b) Improved IRL1
5. Conclusions
The traditional iteratively reweighted -norm minimization algorithm (IRL1) suffers from weak low-frequency sound source identification capability and poor anti-interference performance. To address these limitations, this paper proposes an improved IRL1 algorithm. Unlike traditional methods, this method introduces a log-sum penalty function into the mathematical model of -norm minimization. By constructing a surrogate function to derive a weighting matrix, the problem is transformed into a form that can effectively solve the source strength distribution vector, thereby obtaining its sparse solution. Numerical simulation analysis demonstrates that under both low-frequency and low SNR conditions, the proposed algorithm achieves superior identification results compared to the traditional IRL1 method. The improved IRL1 algorithm resolves the existing algorithm’s inability to adapt to low-frequency scenarios and its weak anti-interference capability. This innovation extends the applicable frequency range of the IRL1 algorithm while further enhancing its spatial resolution.
References
-
P. Gerstoft, C. F. Mecklenbräuker, W. Seong, and M. Bianco, “Introduction to compressive sensing in acoustics,” The Journal of the Acoustical Society of America, Vol. 143, No. 6, pp. 3731–3736, Jun. 2018, https://doi.org/10.1121/1.5043089
-
H. Boche, R. Calderbank, and G. Kutyniok, “Compressed sensing and its applications,” in Applied and Numerical Harmonic Analysis, Cham: Springer International Publishing, 2017, https://doi.org/10.1007/978-3-319-69802-1
-
S. Foucart and H. Rauhut, Applied and Numerical Harmonic Analysis. New York, NY: Springer New York, 2013, https://doi.org/10.1007/978-0-8176-4948-7
-
S. S. Chen, D. L. Donoho, and M. A. Saunders, “Atomic decomposition by basis pursuit,” SIAM Journal on Scientific Computing, Vol. 20, No. 1, pp. 33–61, Jan. 1998, https://doi.org/10.1137/s1064827596304010
-
A. Xenaki, P. Gerstoft, and K. Mosegaard, “Compressive beamforming,” The Journal of the Acoustical Society of America, Vol. 136, No. 1, pp. 260–271, Jul. 2014, https://doi.org/10.1121/1.4883360
-
E. J. Candès, “The restricted isometry property and its implications for compressed sensing,” Comptes Rendus. Mathématique, Vol. 346, No. 9-10, pp. 589–592, Apr. 2008, https://doi.org/10.1016/j.crma.2008.03.014
-
S. G. Mallat and Zhifeng Zhang, “Matching pursuits with time-frequency dictionaries,” IEEE Transactions on Signal Processing, Vol. 41, No. 12, pp. 3397–3415, Jan. 1993, https://doi.org/10.1109/78.258082
-
J. A. Tropp, “Greed is good: Algorithmic results for sparse approximation,” IEEE Transactions on Information Theory, Vol. 50, No. 10, pp. 2231–2242, Oct. 2004, https://doi.org/10.1109/tit.2004.834793
-
D. Needell and R. Vershynin, “Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit,” Foundations of Computational Mathematics, Vol. 9, No. 3, pp. 317–334, 2009.
-
S. Ji, Y. Xue, and L. Carin, “Bayesian compressive sensing,” IEEE Transactions on Signal Processing, Vol. 56, No. 6, pp. 2346–2356, Jun. 2008, https://doi.org/10.1109/tsp.2007.914345
-
D.-Y. Hu, X.-Y. Liu, Y. Xiao, and Y. Fang, “Fast sparse reconstruction of sound field via Bayesian compressive sensing,” Journal of Vibration and Acoustics, Vol. 141, No. 4, Aug. 2019, https://doi.org/10.1115/1.4043239
-
W. Wang and W. M. Tang, “complex sparse signal recovery method based on Bayesian compressive sensing,” Journal of Electronics and Information, Vol. 38, No. 6, pp. 1419–1423, 2016.
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
