Research on optimization of intelligent driving

1. Introduction

With the continuous development of control theory, information technology, and artificial intelligence technology, intelligent vehicles have become one of the hot topics in academic and industrial research. The auto drive system integrates environmental awareness, decision-making planning and motion control functions. Among them, trajectory tracking control is one of the most fundamental and important technologies in intelligent vehicles. In recent years, intelligent vehicles with autonomous driving capabilities have become a research hotspot in the industry. Path tracking control is one of the key core technologies for intelligent vehicles, aiming at designing control laws to enable the vehicle to track a given path. At the same time, intelligent vehicles have the important feature of real-time tracking of paths, with the main goal of reducing deviations from the planned path and driving along the predetermined path by controlling the front wheel angle. The main goal of path tracking control in non extreme working conditions is to achieve high-precision path tracking. During the operation of intelligent vehicles, path tracking control systems can reduce the impact of human factors on driving behavior, reduce the incidence of traffic accidents, and improve road traffic safety. In addition, the path tracking control system can improve transportation efficiency, reduce traffic congestion, and save travel time by optimizing path planning, intelligent traffic signal control, and other methods. With the rapid development of artificial intelligence, the design of intelligent vehicle path tracking control has received great attention from all sectors of society. Therefore, the design of intelligent vehicle path tracking control system is of great significance [1-3].

The problem of vehicle path tracking has been widely studied. A brief review is presented in what follows.

Falcone et al. established an model predictive control (MPC) path tracking controller based on a linear vehicle model, and constrained the tire roll angle to improve the tracking accuracy and stability of the vehicle on low adhesion roads [4]. Fan et al. used fuzzy control method to optimize the prediction time domain and control time domain of MPC controller online [5]. The prediction time domain parameters were adaptively selected based on the lateral and longitudinal vehicle speeds of the vehicle. The optimized MPC controller improved the stability and tracking accuracy of vehicle path tracking. However, online optimization of time-domain parameters would increase the computational complexity of MPC and affect the real-time performance of the controller. Guo et al. studied the integrated strategy of obstacle avoidance path planning and control based on MPC [6]. Guo et al. proposed a control method that combined path tracking control and direct yaw moment coordination [7]. The parameter selection of the controller determined its effectiveness under different speeds and road curvature conditions. Wang et al. studied a parameter adaptive MPC path tracking control method based on fuzzy rules [8]. In this type of research, in order to simplify system modeling, a linear tire model was used to establish a prediction model, and the tire side slip angle was restricted by hard constraints to prevent entering the nonlinear and saturated regions of the tire, failing to effectively utilize the nonlinear dynamic characteristics of the tire. In order to fully utilize the nonlinear dynamic characteristics of tires, some scholars had established time-varying parameter tire dynamics models and designed path tracking MPC controllers. For example, Brown et al. solved the problem of vehicle collision avoidance stability control by obtaining tire lateral stiffness through continuous linearization [9]. Compared to model-based optimization methods such as MPC, the advantage of reinforcement learning based methods is that they do not rely on precise system models or physical modeling of environmental dynamics, and achieve interaction between the agent and the environment through data-driven methods, generating interaction data. Through continuous interaction, iteration, and learning training, the agent can learn the optimal control strategy. This can not only reduce the complexity of trajectory tracking controller design, but also to some extent solve the problem of low trajectory tracking control accuracy and poor robustness in complex working conditions when using state space model-based optimization methods to design trajectory tracking controllers. Reinforcement learning has shown significant advantages in solving trajectory tracking and control problems for mobile vehicles such as robots and intelligent vehicles. For example, Li et al. built a deep reinforcement learning training environment based on an open racing simulator and proposed a deterministic policy gradient based trajectory tracking control strategy for autonomous driving racing vehicles [10]. The predicted trajectory output by the perception module was used as the system state input, and the reinforcement learning control module output the racing vehicle autonomous driving control decision instructions based on trajectory characteristics. This method had better tracking performance than linear quadratic regulator controllers and model predictive controllers when tracking different trajectory curves. Fuchs et al. proposed a racing autonomous driving control strategy based on flexible motion evaluation, which could achieve better track lap times than human drivers by training the racing autonomous driving control strategy with limited computing power [11]. Sun et al. established a time-varying parameter model for the rear wheel and studied the MPC control method based on the lateral force of the front wheel [12]. These methods all established linear tire models with time-varying parameters which could effectively utilize the dynamic characteristics of the nonlinear region of the tire. A robust control scheme was proposed in references [13-17], which expanded the dynamic model and designed a controller for intelligent vehicles even in harsh working conditions where the tire lateral stiffness deviated significantly from its calibration nominal value. This type of method effectively improved the robustness of intelligent vehicle path tracking control, ensuring the control performance of intelligent vehicles under low adhesion and other conditions. However, due to the fact that robust control methods were often studied under the worst-case conditions, the designed controller compromised on control accuracy to ensure robustness, often exhibiting strong conservatism. Sarada Prasad Parida et al. provided prediction and estimation for the multiple transverse cracks in a composite beam using hybrid RNN-mPSO technique [18-21].

The traditional global pseudospectral method has the advantages of simplicity and efficiency, but its performance is not ideal when solving large, complex, and nonsmooth problems. As the number of discrete points increases, it becomes increasingly complex when transformed into corresponding nonlinear programming problems. Because the corresponding control variables may not be continuous when there are different path constraints, the idea of segmented optimization can be introduced into the pseudospectral method to improve algorithm performance.

When using traditional methods to solve the vehicle path tracking problem, there are problems such as long computation time, low computational efficiency, and the need to guess the initial values of the co state equation. The collocation method in the direct method has been widely studied and applied in recent years due to its low sensitivity to initial values and easy convergence, as it does not require the derivation of necessary optimality conditions. The multi-interval Radau pseudospectral method is a type of collocation method that divides time into multiple intervals and approximates the state variables on the LGR (Legendre Gauss Radau) collocation using low order interpolation polynomials in each interval. Compared with the traditional pseudospectral method that applies high-order interpolation polynomials throughout the entire time interval, the multi-interval Radau pseudospectral method discretizes the nonlinear programming problem (NLP) partial derivative matrix, which is sparser and has higher computational efficiency. Based on the multi-interval Radau pseudospectral, this article uses Carsim and MATLAB/Simulink platforms to verify the effectiveness of the method through numerical simulation.

2. Mathematical model of vehicle path tracking problem

2.2. Optimal control object of path tracking problem

The minimum tracking error to complete the path tracking process is determined as the control object.

The cost function is [22]:

3

$J\left(z\right)={\int }_{t_0}^{t_f}\left({\left(\frac{y-y_d}{\widehat{E}}\right)}^2+{\left(\frac{z}{{\widehat{T}}_{sw}}\right)}^2\right)dt={\int }_{t_0}^{t_f}L\left(x,z\right)dt,$

where $y_d$ is the reference path, $\widehat{E}$ is the standard threshold of the lateral distance error of $y-y_d$, where $\widehat{E}$= 0.3 m in this work, and ${\widehat{T}}_{sw}$ is the standard threshold of the steering torque, taken as ${\widehat{T}}_{sw}$= 8 N·m here.

Fig. 14-DOF vehicle model

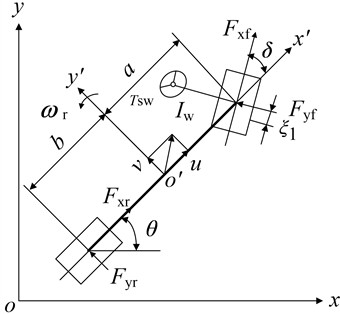
Table 1Simulation parameters

Parameter	Definition	Value
$m$ (kg)	Vehicle mass	1265
$I_z$ (kg∙m2)	Moment of inertia around the z axis	1800
$a$ (m)	Distances of front axle from the center of gravity	1.170
$b$ (m)	Distances of rear axle from the center of gravity	1.195
$k_1$ (N∙rad−1)	Synthesized stiffness of front tire	60042
$k_2$ (N∙rad−1)	Synthesized stiffness of rear tire	109295
$i$	Transmission ratio of the steering system	20
$\mu$	Coefficient of friction	0.8
$I_w$ (kg∙m2)	Moment of inertia of the steering system	16.38
$c_w$ / (N∙m∙s∙rad-1)	Drag coefficient	140
$k_w$ / (N∙m∙rad-1)	Synthesized cornering stiffness	0
${\mathrm{\xi }}_1$ / m	Front wheel aligning arm of force	0.021
$h_g$ (m)	Height of the center gravity	0.53

3. Control method of vehicle path tracking problem

3.1. Multiple phase Radau pseudospectral method

This article uses the multiple phase pseudospectral method to solve the problem of vehicle trajectory tracking. For ease of description, this section takes the general form of Bolza type optimal control problem as an example to introduce the multiple phase pseudospectral method. The Bolza type problem can be described as: solving the control variable $u\left(t\right)\in R^m$ to minimize the following objective function:

10

$J=M\left(x\left(t_0\right),t_0,x\left(t_f\right),t_f\right)+{\int }_{t_0}^{t_f}L\left(x\left(t\right),u\left(t\right),t\right)dt.$

The state equation is:

11

$\dot{x}=f\left(x\left(t\right),u\left(t\right),t\right),\left(t\in \left[t_0,t_f\right]\right).$

The endpoint condition is:

12

$e\left(x\left(t_0\right),t_0,x\left(t_f\right),t_f\right)=0.$

The path constraint is:

13

$c\left(x\left(t\right),u\left(t\right),t\right)\le 0,\left(t\in \left[t_f,t_f\right]\right).$

The continuous optimal control problem described by Eqs. (10)-(13) is called the Bolza type optimal control problem.

In order to facilitate the discretization of the optimal control problem using the pseudospectral method, it is necessary to transform the time interval $t\in [t_0,t_f]$ of the original optimal control problem to $\tau \in [-\mathrm{1,1}]$. The transformation method is as follows:

14

$t=\frac{t_f-t_0}{2}\tau +\frac{t_f+t_0}{2}.$

The range of variation of the integral variable $\tau \in [-\mathrm{1,1}]$ is divided into $K$ grid intervals $I_k=[T_{k-1},T_K]$$(k=1,\cdots ,K)$; where $1=T_0<T_1<\cdots <T_K=T_f=1$. $x^{\left(k\right)}\left(\tau \right)$ is set as a state variable on the interval $I_k(k=1,\cdots ,K)$, the state variable can be approximated as:

15

$x^{\left(k\right)}\left(\tau \right)\approx y^{\left(k\right)}\left(\tau \right)=\sum _{j=1}^{N_k+1}{x}_j^{\left(k\right)}{l}_j^{\left(k\right)}\left(\tau \right),$

where $y^{\left(k\right)}\left(\tau \right)$ is an approximate function of $x^{\left(k\right)}\left(\tau \right)$; $x_j^{\left(k\right)}$ is the value of the state variable at the discrete node $T_K$. And the expression $l_j^{\left(k\right)}\left(\tau \right)$ is the Lagrange basic polynomial as follows [23]:

16

$l_j^{\left(k\right)}\left(\tau \right)={\prod }_{l=1,l\ne j}^{N_k+1}\frac{\tau -{\tau }_l^{\left(k\right)}}{{\tau }_j^{\left(k\right)}-{\tau }_l^{\left(k\right)}},$

where the nodes $\left({\tau }_1^{\left(k\right)},\cdots ,{\tau }_{N_k}^{\left(k\right)}\right)$ are $N_k$ Legendre Gauss Radau (LGR) collocation points on the interval $I_k=[T_{k-1},T_K]$. But the right endpoint ${\tau }_{N_k+1}^{\left(k\right)}=T_k$ of the interval $I_k$ is not an LGR collocation point.

Differentiating $y^{\left(k\right)}\left(\tau \right)$ with respect to $\tau$ in Eq. (15), Eq. (17) can be obtained:

17

$\frac{d{y}^{\left(k\right)}\left(\tau \right)}{d\tau }=\sum _{j=1}^{N_k+1}{x}_j^{\left(k\right)}\frac{d{l}_j^{\left(k\right)}\left(\tau \right)}{d\tau }.$

By combining Eq. (11) and Eq. (17), the discrete form of the state equation on the interval $I_k(k=1,\cdots ,K)$ can be obtained as follows:

18

$\sum _{j=1}^{N_k+1}{D}_{ij}^{\left(k\right)}{x}_j^{\left(k\right)}-\frac{t_f-t_0}{2}f\left(x_i^{\left(k\right)},u_i^{\left(k\right)},{\tau }_i^{\left(k\right)}\right)=0,\left(i=1,\cdots ,N_k\right),$

where the elements of the LGR differential matrix on interval $I_k$ are $D_{ij}^{\left(k\right)}=d{l}_j^{\left(k\right)}\left({\tau }_i^{\left(k\right)}\right)/d\tau$$(i=1,\cdots ,N_k;j=1,\cdots ,N_k+1)$; $u_i^{\left(k\right)}\left(i=1,\cdots ,N_k\right)$ is the discrete value of the control variable $u^{\left(k\right)}\left(\tau \right)$.

The discrete form of objective function (Eq. (10)) is:

19

$J\approx M(x_1^{\left(1\right)},t_0,x_{N_K+1}^{\left(K\right)},t_f)+\sum _{k=1}^{k=1}\sum _{j=1}^{j=1}\frac{t_f-t_0}{2}{\omega }_j^{\left(k\right)}L\left(x_j^{\left(k\right)},u_j^{\left(k\right)},{\tau }_j^{\left(k\right)}\right),$

where ${\omega }_j^{\left(k\right)}$ is the LGR weight coefficient corresponding to ${\tau }_j^{\left(k\right)}$.

The discrete form of the endpoint condition (Eq. (12)) is:

20

$e\left(x_1^{\left(1\right)},{\tau }_0,x_{N_K+1}^{\left(K\right)},{\tau }_f\right)=0.$

The discrete form of path constraint (Eq. (13)) is:

21

$c\left(x_i^{\left(k\right)},u_i^{\left(k\right)},{\tau }_i^{\left(k\right)}\right)\le 0,\left(i=1,\cdots ,N_k\right).$

Due to the fact that the right endpoint ${\tau }_{N_k+1}^{\left(k\right)}=T_k$ of interval $I_k$ is not an LGR collocation, in order to make the state variables be continuous in adjacent intervals, it is necessary to satisfy:

22

$x_{N_k+1}^{\left(k\right)}=x_1^{(k+1)},\left(k=1,\cdots ,K-1\right).$

The constraint can be eliminated using the same variable to represent $x_{N_k+1}^{\left(k\right)}$ and $x_1^{(k+1)}$.

The discrete optimal solution of the path tracking optimization problem can be obtained by using numerical methods to solve the NLP problems described in Eqs. (18)-(22).

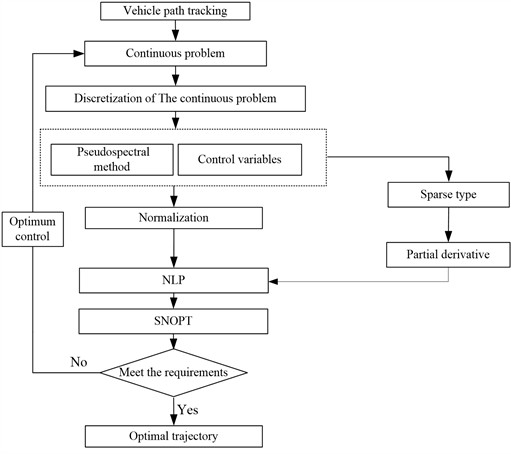
Fig. 2Flow chart of the algorithm

4. Numerical simulations and experimental verification

4.1. Numerical simulations

This section uses CarSim to verify the feasibility and effectiveness of the optimal control problem of trajectory tracking.

Fig. 3 is the reference path of double lane changing road.

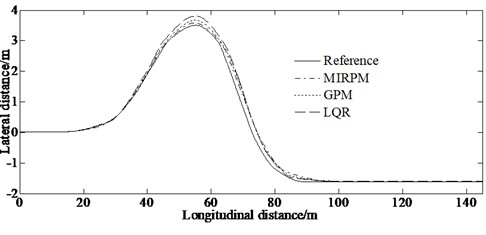
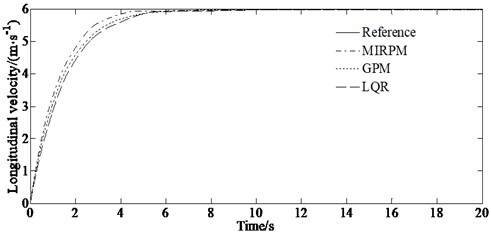
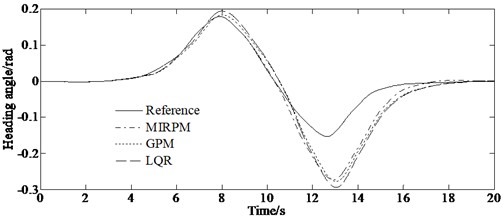
Fig. 4 is the simulation result compared with the GPM and linear quadratic regulator (LQR) methods under the condition of double lane changing road.

Fig. 3Reference path of double lane changing road

Fig. 4Simulation result under the condition of double lane changing road

a) Lateral distance

b) Longitudinal velocity

c) Heading angle

It can be seen from Fig. 4(a) that the path tracking controlled by the method proposed in this article satisfies the path constraint requirements. The vehicles can perform path tracking well, but it is prone to slight deviations at intersections of straight and curved roads. This is due to the short transition distance and high speed between the double lane lines. However, the vehicle path can track the expected path trend well, thus verifying the good path tracking control ability of the method in the paper. It can be seen from Fig. 4(b) that the vehicle can ensure smooth changes in speed during turning, reducing speed fluctuations and improving driving stability. And the three control method are able to stabilize the longitudinal velocity and reach the reference speed. Fig. 4(c) indicates that the controller algorithm can control the vehicle to travel on double lane roads with large changes in road curvature, and can track the target path well. While ensuring accurate tracking of the target path, it further improves the safety and stability of vehicle travel. The reason is that the use of full optimization results to provide initial values has accelerated the convergence speed. Meanwhile, online updates of the algorithm can significantly improve the accuracy of trajectory tracking with minimal computational cost.

4.2. Control performance

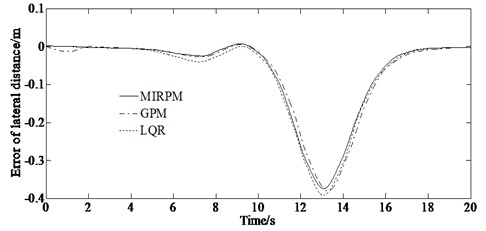
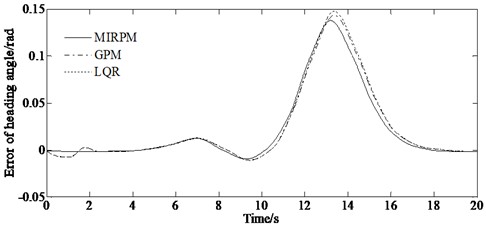
The changes in lateral and heading error of vehicle path tracking are shown in Fig. 5. It can be observed that compared with the lateral error increases from 0 to 0.38 m and gradually decreases, while the magnitude of heading error fluctuates between 0 and 0.15 rad. The average values of lateral error and heading error are calculated to be 0.0912 m and 0.0263 rad. It is possible to ignore the suspension design and the rolling resistance when building mathematical models. However, the lateral error and heading error of path tracking are controlled within a small error range during the path tracking process. And also, compared with the traditional GPM and LQR method, the tracking error of the proposed is smallest. This proves that the proposed control method can effectively ensure the control accuracy of vehicle path tracking. The deviation in lateral position is minimized, and the effect of quickly tracking the target path can be achieved.

Fig. 5Comparison results of the control performance between MPRPM, GPM and LQR

a) Error of lateral distance

b) Error of heading angle

4.3. Experimental verification

To verify the tracking accuracy of the MIRPM algorithm, a virtual test adopting the Carsim software is conducted. By building a vehicle dynamic model on the Carsim platform, the state parameters of the vehicle are outputted in double lane changing road to verify the superiority of the algorithm proposed in this paper.

The virtual test results in Fig. 6 show that the intelligent vehicle path tracking control method proposed in this paper can control the vehicle to quickly and stably track the target path, and has good tracking accuracy. This is because that the proposed method can quickly update the trajectory, eliminate the influence of accumulated errors, and significantly improve the accuracy of car trajectory tracking. Meanwhile, there is a certain degree of error between the simulated values and the virtual test values, which is caused by two reasons; On the one hand, one characteristic of the multi-interval pseudospectral method is to improve optimization speed by sacrificing discretization accuracy; On the other hand, the vehicle model does not take into account the nonlinearity of the suspension system. However, the trend of changes in simulation values and virtual test values is consistent, indicating the effectiveness of the proposed method.

Fig. 6Experimental results of lateral velocity and yaw rate

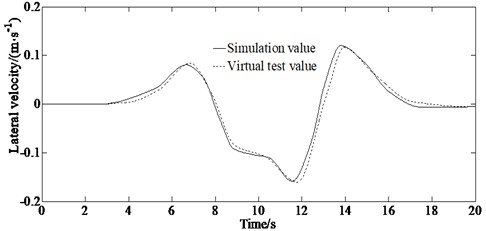
a) Lateral velocity

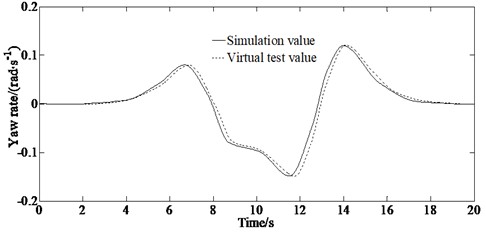
b) Yaw rate

5. Conclusions

In order to solve the problem of multiple constraints and low accuracy in the process of intelligent vehicle path tracking, this paper applies the multi-interval Radau pseudospectral method based on the 4-DOF vehicle motion model to transform the optimal control problem of vehicle path tracking into a nonlinear programming problem and solves it using the sequential quadratic programming method. A simulation experiment is conducted using a joint simulation model of CarSim and Simulink, and the results showed that the proposed control method can control the lateral error and heading error in the vehicle path tracking process within a small range and converge, indicating that the accuracy and reliability of path tracking can be guaranteed.

The problem of path tracking control is studied in this paper, but the stability control of intelligent vehicles during driving has not been considered. At the same time, the influence of model uncertainty, nonlinear interference and system delay on control has not been considered in this paper. In the future, in-depth research will be conducted on the above problems.