Simulation of motion trajectories and kinematic characteristics of an oscillatory system with a planetary-type vibration exciter

1. Introduction

Vibratory systems play a significant role across various industrial sectors, and their effective operation often hinges on achieving specific dynamic states, such as resonance. The optimal synthesis and implementation of resonant vibratory systems are key areas of study to maximize efficiency [1]. However, system design can also target other dynamic regimes, like anti-resonance, which has been investigated in various vibratory machines employing specific exciters like passive auto-balancers [2]. The dynamics of resonant systems, including single-mass machines, can be complex, involving phenomena like Sommerfeld effect when utilizing vibration exciters designed for targeted action [3]. The interaction between rotational components and vibrations gives rise to interesting behaviors, such as the vibrational capture of an unbalanced rotor’s rotation [4], and the generation of slow oscillations in systems driven by inertial vibration exciters [5]. Research continues to refine the understanding and design of inertial exciters, examining the dynamics of specific configurations like enhanced coaxial inertial types for vibratory machines [6]. The practical application of controlled oscillations is diverse, including the transportation of objects on inclined planes through manipulated dynamic friction [7] and the operation of oscillating conveyors, where determining kinematic and dynamic characteristics is crucial [8].

Different mechanical structures are employed for vibration excitation. Crank-link mechanisms, for instance, are used in industrial screens, with studies focusing on their vibration characteristics and parameter optimization [9]. Controllable crank mechanisms offer adaptability for exciting oscillations in various vibratory equipment [10]. The dynamic behavior of machinery like vibratory screening conveyors equipped with crank-type exciters has been analyzed [11], extending to dynamic analyses of multi-mass systems utilizing mechanisms like twin crank-slider exciters [12]. While distinct from exciters, the related field of planetary gear trains also involves complex vibration modeling, such as analyzing torsional vibrations in differential planetary systems [13]. Turning specifically to planetary mechanisms used as vibration exciters, research has explored designs like adjustable planetary vibratory exciters incorporating chain gears [14]. The broader analysis of vibration exciters’ working processes aims to improve efficiency for applications in demanding fields like construction and road machines [15]. Recent work has specifically focused on the capabilities of planetary-type exciters, demonstrating their ability to generate various complex motion paths in single-mass vibratory systems through symmetric designs [16]. Building on this, detailed kinematic analysis and justification of geometrical parameters for planetary-type mechanisms used to actuate inertial vibration exciters have been performed [17]. Further extending this line of inquiry, force analyses of these planetary-type mechanisms in enhanced vibration exciters have been conducted [18].

This established body of work, exploring diverse vibratory systems, excitation methods, and detailed analyses of planetary mechanisms [13-18], sets the stage for the current study. While kinematic and force analyses of planetary exciters have been undertaken [17], [18], and their potential for generating varied motion paths has been identified [16], a dedicated simulation (virtual experiments) focusing on the resultant motion trajectories and detailed kinematic characteristics of the oscillatory system they drive is needed for a comprehensive understanding. Therefore, this paper presents a simulation study to investigate these aspects, aiming to elucidate the operational dynamics of oscillatory systems equipped with planetary-type vibration exciters.

2. Research methodology

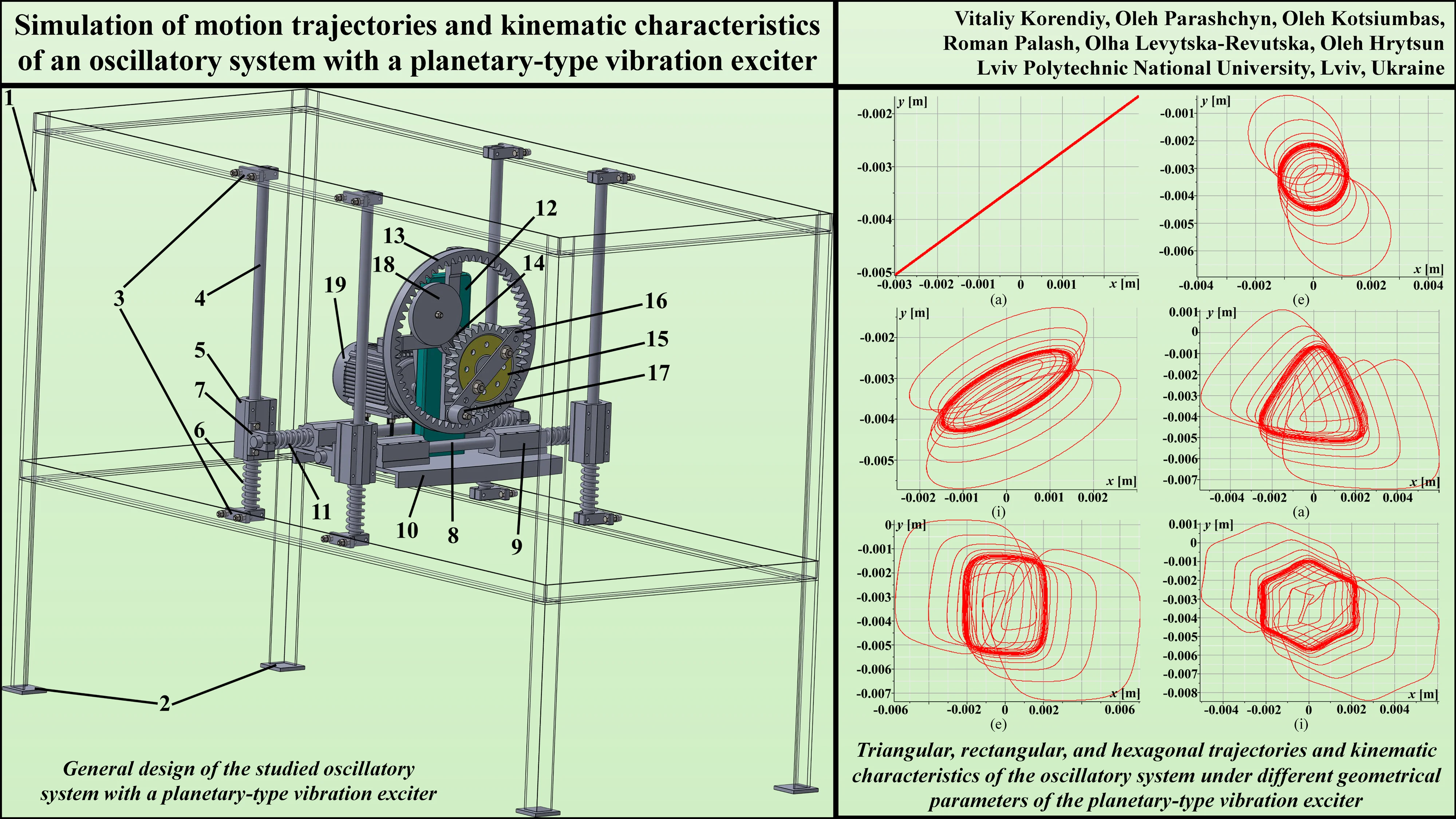
The studied mechanical oscillatory system was designed using the SolidWorks software and is presented in Fig. 1. The system is mounted on a frame 1, which is fixed to the foundation via the plates 2. Vertical guides 4 are rigidly attached to the frame 1 using clamps 3. Linear bearing assemblies 5 can slide along the guides 4 and their movement is constrained by the springs 6. Clamps 7, which support the horizontal motion guides 8, are attached to the bearing assemblies 5. Linear bearing assemblies 9, upon which the oscillating plate 10 is fixed, can slide along the horizontal guides 8. The horizontal movement of the bearing assemblies 9 with the plate 10 is limited by the springs 11. The vibration exciter bracket 12, with the ring gear (annulus) 13 of the planetary-type mechanism fixed onto it, is mounted on the plate 10. The carrier 14 drives the planet gear (satellite) 15, onto which the lever 16 with an attached imbalanced body 17 is mounted. On the opposite side of the carrier, a counterweight (balancer) 18 can be installed to balance the planet gear 15 of the planetary-type mechanism relative to the carrier’s 14 axis of rotation. The carrier 14 is driven by an electric motor 19 via a toothed belt drive (not shown in the figure).

The investigated oscillatory system operates as follows. The rotary motion from the shaft of the electric motor 19 is transmitted via a toothed belt drive to the shaft of the carrier 14 of the planetary-type excitation mechanism. The carrier drives the planet gear 15, around whose axis of rotation the imbalanced body 17 moves. Inertial forces acting on the imbalanced body 17 are transmitted through the lever 16 and the carrier 14 to the bracket 12 and, consequently, to the plate 10 of the mechanical oscillatory system. The latter, undergoing planar motion, can oscillate along a specific trajectory that depends on the geometric dimensions of the planetary mechanism, as well as on the inertial and stiffness parameters of its components (oscillating bodies and springs). Based on the authors’ previous investigations [16-18], virtual experiments will be conducted in this research using the “Motion Analysis” application of the SolidWorks software. These experiments aim to substantiate the capability of generating circular, elliptical, rectilinear, and polygonal motion trajectories for the oscillating plate 10, which could potentially serve in the future investigations as the working element of various types of vibratory technological equipment (such as a conveying tray, sieve, screen, compacting or tamping plate, etc.).

Fig. 1General design of the studied oscillatory system with a planetary-type vibration exciter

3. Results of computer simulations

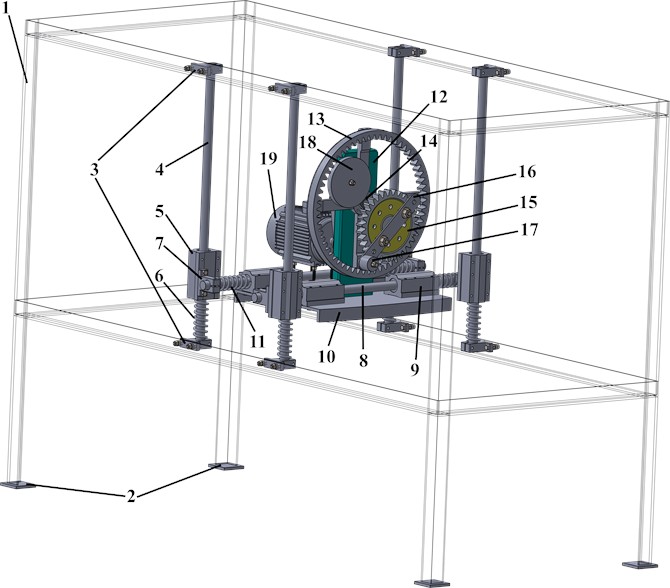
Based on the authors’ previous investigations [16]–[18] and taking into account the designed 3D-model of the mechanical oscillatory system with the planetary-type vibration exciter, let us perform computer simulation of the system motion under the following geometrical, inertial, excitation, stiffness, and damping parameters (see Fig. 2): angular velocity (rotational frequency) of the carrier $\omega =$ 157 rad/s (25 Hz), reduced stiffness coefficients of vertical and horizontal springs $k=$ 30000 N/m, reduced damping coefficients for the vertical and horizontal motion of the system $c=$ 100 N·s/m, total mass of the oscillating bodies $M=$ 10 kg, mass of the imbalanced body $m=$ 0.1 kg, length of the carrier $l=$ 0.1 m. In addition, let us consider the following parameters: 1) to generate the oscillations with linear trajectory: angular velocity (rotational frequency) of the planet gear ${\omega }_1=$ 314 rad/s (50 Hz), eccentricity of the imbalanced rotor $l_1=$ 0.1 m, mass of the planet gear $m_1=$ 0 kg; 2) to generate the oscillations with circular trajectory: ${\omega }_1=$ 314 rad/s (50 Hz), $l_1=$ 0 m, $m_1=$ 0 kg; 3) to generate the oscillations with elliptical trajectory: ${\omega }_1=$ 314 rad/s (50 Hz), $l_1=$ 0.05 m, $m_1=$ 0 kg; 4) to generate the oscillations with triangular trajectory: ${\omega }_1=$ 471 rad/s (75 Hz), $l_1=$ 0.03 m, $m_1=$ 0.05 kg; 5) to generate the oscillations with rectangular trajectory: ${\omega }_1=$ 628 rad/s (100 Hz), $l_1=$ 0.02 m, $m_1=$ 0.1 kg; 6) to generate the hexagonal trajectory oscillations: ${\omega }_1=$ 942 rad/s (150 Hz), $l_1=$ 0.015 m, $m_1=$ 0.1 kg.

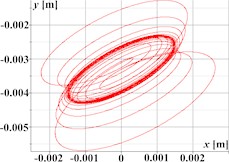
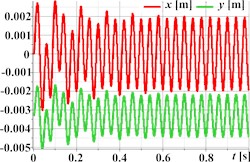
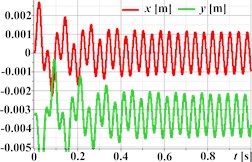
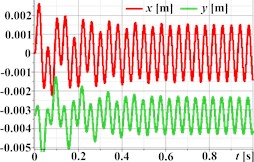
Fig. 2 illustrates the simulated kinematic characteristics of a single-mass oscillatory system actuated by a planetary-type vibration exciter under three different operational regimes, demonstrating the exciter’s versatility. The first set (Figs. 2(a)-(d)) corresponds to rectilinear motion, clearly shown by the straight-line trajectory (Fig. 2(a)) and the in-phase, periodic, and roughly sinusoidal time dependencies of displacement (Fig. 2(b)), velocity (Fig. 2(c)), and acceleration (Fig. 2(d)) for both horizontal (Ox) and vertical (Oy) components. The second set (Figs. 2(e)-(h)) is intended to represent circular trajectory oscillations, centered around approximately (0, –0.0035) m; this path is reflected in the periodic, sinusoidal, and out-of-phase waveforms for displacement (Fig. 2(f)), velocity (Fig. 2(g)), and acceleration (Fig. 2(h)). The third set (Figs. 2(i)-(l)) depicts elliptical trajectory oscillations, with a stable, tilted elliptical path shown in Fig. 2(i) centered similarly to the second set. The corresponding kinematic plots (Figs. 2(j)-(l)) show periodic, roughly sinusoidal waveforms with the characteristic phase difference between the horizontal (Ox) and vertical (Oy) components required to generate the observed elliptical motion.

Fig. 2Linear, circular, and elliptical trajectories and kinematic characteristics of the oscillatory system under different geometrical parameters of the planetary-type vibration exciter

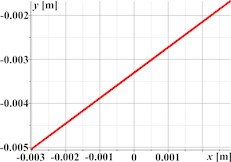
a)

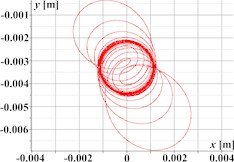
e)

i)

b)

f)

j)

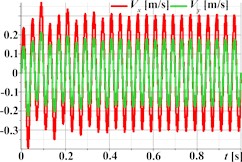
c)

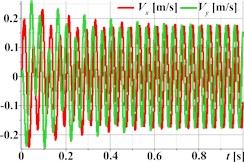
g)

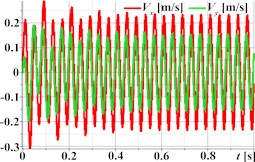
k)

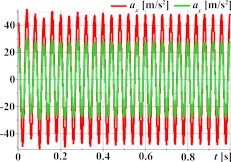
d)

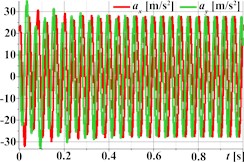
h)

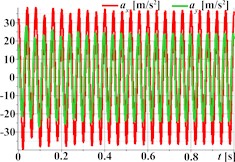
l)

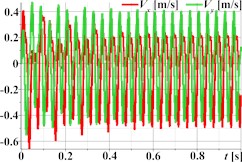
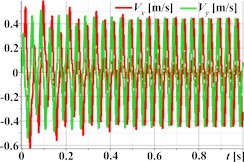
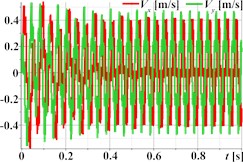
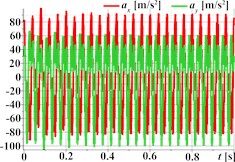
Fig. 3 demonstrates the capability of the planetary-type vibration exciter to generate complex, polygonal motion paths for the single-mass oscillatory system, illustrated through three distinct examples. The first set (Figs. 3(a)-(d)) corresponds to parameters aimed at producing triangular trajectory oscillations, with Fig. 3(a) showing a stable path approximating a triangle with rounded vertices; the associated kinematic time dependencies for displacement (Fig. 3(b)), velocity (Fig. 3(c)), and acceleration (Fig. 3(d)) are periodic but clearly non-sinusoidal, reflecting the sharp changes in direction inherent in the path. Similarly, the second set (Figs. 3(e)-(h)) represents rectangular trajectory oscillations, where the trajectory in Fig. 3(e) resembles a rounded square or rectangle, again mirrored by complex, periodic, and non-sinusoidal kinematic profiles (Fig. 3(f)-(h)). The third set (Figs. 3(i)-(l)) achieves hexagonal trajectory oscillations, displaying a distinct, rounded hexagonal path in Fig. 3(i), which correlates with complex, periodic kinematic time dependencies (Figs. 3(j)-(l)) exhibiting particularly high peak accelerations (Fig. 3(l)) due to the higher frequency components needed to trace the hexagonal shape. In all cases, the complex trajectories result in non-sinusoidal kinematic characteristics with significant harmonic content.

Fig. 3Triangular, rectangular, and hexagonal trajectories and kinematic characteristics of the oscillatory system under different geometrical parameters of the planetary-type vibration exciter

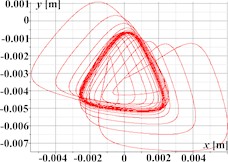
a)

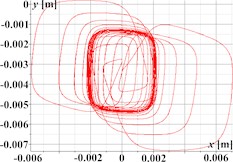
e)

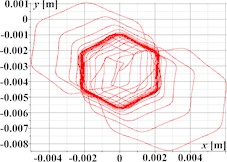
i)

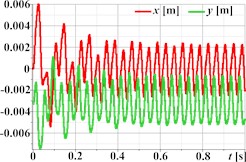
b)

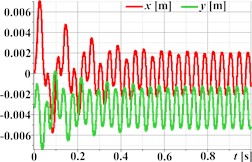
f)

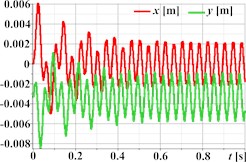
j)

c)

g)

k)

d)

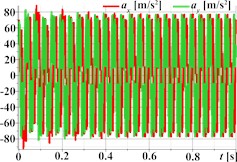
h)

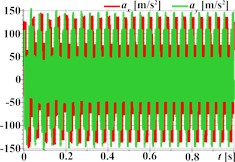
l)

4. Discussion of possible applications

The ability to generate diverse and specific motion trajectories for the working members of vibratory equipment, as demonstrated by mechanisms like planetary exciters [16, 17], opens up significant possibilities for optimizing various technological processes and potentially enabling entirely new functionalities beyond those achievable with traditional sinusoidal or linear motions.

Linear trajectories, representing the simplest form of controlled vibration, are fundamental for tasks primarily requiring unidirectional action. Their main applications are found in vibratory conveyors and feeders designed to transport (move) materials along a straight path. They are also employed in basic linear screening machines [9], where the primary goal is material transportation across the screen surface coupled with some degree of stratification, and in elementary compaction tasks that necessitate predominantly vertical forces [15]. However, while efficient for simple transportation, pure linear motion might prove less effective for processes demanding significant particle agitation, efficient stratification, or complex material interactions, such as high-efficiency screening or intensive mixing of various materials such as powders, granules, aggregates, ores, fertilizers, food ingredients, pharmaceuticals, chemicals, and construction mixtures, etc.

Circular trajectories provide constant agitation in all horizontal directions, making them suitable for different applications. This motion is widely utilized in circular vibratory screens and separators (often called “circular throw screens”) [11], where it effectively promotes particle stratification and facilitates the passage of material through screen meshes. Circular motion is also advantageous in vibratory finishing, lapping, and polishing machines, ensuring uniform surface treatment. Furthermore, it finds use in certain types of mixers for granular materials and in some designs of circular compactors. A key consideration is that pure circular motion lacks a directional conveying component unless supplemented by an inclined surface of the working member.

Elliptical trajectories offer a versatile blend of linear and circular motion characteristics, providing both a conveying action and enhanced agitation simultaneously [8]. This makes them highly common in modern elliptical motion screens, conveyors, and feeders. The angle and aspect ratio (major-to-minor axis ratio) of the ellipse can often be automatically or manually adjusted [10], allowing operators to fine-tune the conveying speed and screening efficiency to suit different materials, particle sizes, and screen inclinations. Elliptical motion is also applied in specialized vibratory feeders requiring specific material flow behaviors and potentially in compaction equipment where a directional force bias combined with effective agitation is beneficial [7].

The capability to generate more complex polygonal trajectories, such as those approximating triangles, rectangles, or hexagons, represents a newer frontier with intriguing potential applications, although they are less established than simpler paths. These complex paths inherently involve relatively sharp changes in direction (even if mechanically smoothed into rounded vertices) and often result in non-sinusoidal velocity and acceleration profiles [16, 17].

The unique characteristics of polygonal motions suggest several potential benefits. In screening and sieving, the enhanced agitation and sharper directional changes could be more effective at dislodging near-size particles from screen apertures, thus reducing blinding or pegging, potentially surpassing the performance of smoother circular or elliptical motions for “difficult” materials, e.g., extremely dry and fine powders, damp clays, flaky aggregates, etc. In compaction and densification processes, the multi-directional impacts within each cycle, possibly including focused high-acceleration events corresponding to the trajectory’s “corners”, might lead to faster or denser packing of granular materials or powders. For mixing, the complex agitation patterns could enhance blend homogeneity or speed. While likely less efficient for simple bulk transport, these paths might offer advantages in specialized conveying scenarios involving sticky materials or requiring specific particle orientation. Potential applications could also exist in surface treatment processes requiring more aggressive or spatially varied action.

However, implementing complex polygonal trajectories also presents challenges. Generating these paths often involves significant non-sinusoidal forces and higher peak accelerations compared to simpler motions, placing greater demands on the machine’s structural integrity, bearings reliability, and drive system power. Energy consumption might also be higher. Therefore, while the potential benefits are considerable, the practical application requires careful design and thorough investigation to determine the true process advantages and ensure mechanical strength and reliability. The optimal trajectory for any given task will ultimately depend on a detailed analysis of the physicochemical and mechanical properties of the specific material, technological process objectives, and economic considerations. Further research and application-specific development are needed to fully harness the potential of these advanced motion capabilities.

5. Conclusions

The paper investigated the motion trajectories and kinematic characteristics of a single-mass oscillatory system driven by a planetary-type vibration exciter through virtual experiments conducted using the SolidWorks Motion Analysis application. The primary objective was to substantiate the feasibility of utilizing planetary mechanisms to generate diverse and controllable vibration patterns for potential application in various vibratory technological equipment. The simulation results successfully demonstrated the versatility of the planetary-type exciter. By adjusting key geometric and kinematic parameters, specifically the planet gear’s angular velocity, the lever length/eccentricity, and the planet gear mass, while maintaining a constant carrier angular velocity, it was possible to generate a wide range of motion trajectories for the oscillatory system. The study confirmed the generation of: 1) rectilinear trajectory oscillations, characterized by in-phase, roughly sinusoidal kinematic components; 2) circular trajectory oscillations, resulting in periodic, sinusoidal displacements, velocities, and accelerations with the expected phase difference between orthogonal components; 3) elliptical trajectory oscillations, also showing roughly sinusoidal kinematics with appropriate phase shifts; 4) complex polygonal trajectories of oscillations, including approximations of triangular, rectangular, and hexagonal trajectories.

Qualitatively, it was observed that while simpler trajectories (rectilinear, circular, elliptical) produced relatively smooth, near-sinusoidal kinematic profiles, the generation of polygonal paths resulted in complex, non-sinusoidal time dependencies for displacement, velocity, and especially acceleration, indicating the presence of significant higher harmonics. These findings confirm the potential of planetary-type exciters as versatile actuators for vibratory equipment, capable of producing specific, technologically required motion paths beyond simple linear or circular oscillations. This research contributes to the further development of methods for exciting predictable oscillations of the working bodies of various vibratory equipment.

Future research directions could include experimental validation of these simulation results using a physical prototype. Further work could also focus on optimizing the planetary mechanism parameters to achieve sharper polygonal trajectories or minimize unwanted vibrations. Additionally, investigating the dynamic forces transmitted to the frame and foundation, and applying the methodology to model specific technological processes like material conveying or screening with these generated trajectories, would be valuable extensions.