Study on the variation mechanism of non-linear stiffness of rubber O-ring

2.1. Hyperelasticity principal model theory

Rubber is a hyperelastic approximately incompressible material, and the intrinsic relationship of rubber materials can be described according to the strain energy function based on the image-only theory. The image-only theory assumes that rubber is isotropic in the undeformed state as well as during deformation. Mooney [13, 17] derived the strain energy function based on the image-only theory of large elastic deformation as:

where, ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ is the main stretch ratio in all three directions.

Rivlin [13, 17] introduced strain invariants into the strain energy function. Based on the above assumptions, the strain energy function is considered to be symmetric with respect to the three principal stretch ratios, i.e., changing the sign of the principal stretch ratios has no effect on the strain energy function. In order to satisfy the boundary condition that the strain energy is zero at zero strain $\left({\lambda }_1={\lambda }_2={\lambda }_3=1\right)$, the strain energy function is given as:

where, $I_1$, $I_2$, $I_3$, are first-, second-, and third-order strain invariants; $D_i$ is a material constant; $J$ is volume ratio; $l_i$ is the original length in the direction of the main axis; $\mathrm{\Delta }{l}_i$ is the length increment in the direction of the main axis. Due to the incompressibility of rubber, ${\lambda }_1^2{\lambda }_2^2{\lambda }_3^2=1$.

Based on the intrinsic model of rubber derived by Rivlin, various other forms of strain energy functions have been developed. There are Mooney-Rivlin model, Yeoh model, Neo-Hookean model, etc.; for general rubber materials, Mooney-Rivlin model can more accurately describe the performance of rubber materials with deformation less than 150 % [19], and is suitable for finite element analysis. Therefore, the Mooney-Rivlin model is chosen to simulate the superelastic characteristics of O-rings, and the first two items are expanded by taking $N=$1 on the basis of the Rivlin model, i.e., it is the Mooney-Rivlin model, and its strain energy function is:

where, $C_{10}$ and $C_{01}$ are rubber material parameters.

For incompressible rubber materials (Poisson’s ratio $\upsilon \approx$ 0.5), the shear modulus $G$ is related to the elastic modulus $E$ at small strains as follows:

When Poisson’s ratio $\upsilon$ is approximately taken as 0.5, it can be obtained that $E=3G$, and at the same time $G=2(C_{10}+C_{01})$, it can be obtained that the elastic modulus of the rubber material has the following relationship with the material parameters:

In literature [15], the relationship between IRHD hardness, $H_r$, and elastic modulus, $E$, was fitted from experimental data as:

According to literature [17], when $C_{01}/C_{10}=$0.25 and the hardness of the O-ring is 70 A, $C_{10}=$0.9284 MPa and $C_{01}=$0.2321 MPa are obtained.

2.2. O-ring damper structure

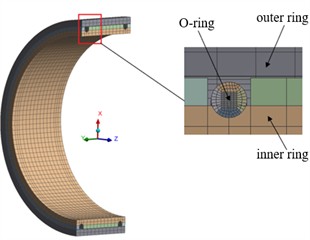
In this paper, the O-ring damper structure used to match an engine, damper inner and outer ring between the arrangement of 2 rings O-ring (due to the symmetry of the 2-ring O-ring structure, in the schematic diagram only indicates a single O-ring) local structure schematic shown in Fig. 1. Among them, the O-ring material is fluorine rubber, the inner and outer sides of the O-ring are the inner and outer rings of the damper, the material of the inner and outer rings is structural steel, and the part of the geometric model that overlaps is the O-ring’s excess. The parameters of the structural part of the damper are shown in Table 1.

2.3. O-ring static stiffness finite element analysis

2.3.1. Modeling and meshing

In this paper, the finite element software Ansys is used to simulate the static characteristics of the O-ring damper, and its three-dimensional model is shown in Fig. 2. In order to improve the calculation speed, the inner and outer rings of the damper are simplified. The bearing and elastic support are simplified as the inner ring, the magazine is simplified as the outer ring, two symmetrically positioned O-rings are mounted on the grooves of the inner ring, and the oil supply holes and rounded corners, Ignore the oil supply holes and rounded corners which have less effect on stiffness, which have a small influence on the stiffness, are ignored. In order to avoid the deformation of the inner and outer rings having a large impact on the stiffness of the O-ring, the modulus of elasticity of the inner and outer rings is much larger than that of the O-ring, which is treated as a rigid body.

Fig. 1Structure diagram of O-ring damper

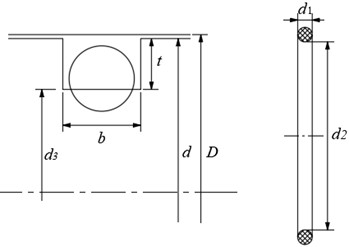
Table 1Structural parameters of O-ring damper

Inner ring outer diameter $d$	Inner diameter of outer ring $D$	Bottom diameter of groove $D_3$	Groove depth $\mathrm{T}$	Groove width $b$	Inner diameter of O-ring $d_2$	O-ring cross-sectional diameter $d_1$
75	75.22	72.2	1.4	2.15	71	1.8

To facilitate meshing and ensure mesh quality, the O-ring is split from the inner ring of the damper. The cell type is selected as 186 cells. The mesh is made of hexahedral cells, and the mesh is encrypted for the cross section of the O-ring. After the mesh-independence verification, the static stiffness of the O-ring tends to be stabilized when the circumferential mesh size of the O-ring is 0.5 mm and the cross-section mesh size is 0.2 mm. Considering the computational accuracy as well as the computational resources, the circumferential mesh of the O-ring is selected to be 0.5 mm, and the cross-section mesh to be 0.2 mm.

2.3.2. Contact setup

There is contact between the O-ring and the inner surface of the outer ring and the groove. As the outer ring squeezes the rubber O-ring to different degrees, the area of the contact surface between the O-ring and the outer ring and the groove changes all the time, and there is a high degree of non-linearity in this contact. Applying the three-dimensional surface contact units CONTA174 and TRAGE170 to establish contact pairs at the O-ring and the inner and outer rings, the surface of the O-ring is used as the contact surface, and the surface in contact with it is used as the target surface. There is permeability between the contact pairs, and the smaller the permeability tolerance is, the higher the computational accuracy is, and at the same time, the more difficult it is to converge. Considering the computational accuracy of the model and the convergence problem, the contact algorithm adopts the augmented Lagrangian method, and the permeability tolerance is taken as 0.01 mm.

Fig. 2Three-dimensional model of O-ring damper

a) Finite element modeling

b) Schematic diagram of gridding

2.3.3. Boundary conditions and numerical solution

According to the assembly and loading process of the O-ring, the loading step is divided into two steps, as shown in Fig. 3.

Fig. 3Assembly and loading process of the O-ring

In the first step, a geometric modeling of interference is used to simulate the interference assembly of the O-ring with the inner ring. The surface of the inner ring of the damper is fixedly supported, and the sides of the outer ring are free in the radial direction, constraining the freedom in the remaining two directions. In the second step, the extrusion process of the outer ring on the O-ring is simulated. In order to prevent the force applied to the outer ring from being too large to cause the inner and outer rings to collide, which would cause the stiffness to vary greatly, the displacement load is used instead of the force load. Considering that the actual gap between the inner and outer rings is 0.11 mm, a displacement load of 0.1 mm linearly increasing along the $x$-direction is applied to the outer surface of the outer ring.

2.3.4. Analysis of numerical simulation results

The displacement cloud of the O-ring damper after the interference assembly as well as the compression process is shown in Fig. 4. The inner ring of the damper is fixed during assembly, and the radial reaction force on the outer ring when the O-ring is recovered from interference is uniformly distributed and counteracts each other, so that the inner and outer rings do not move and the radial reaction force on the outer ring is zero. When the outer ring is compressed in the $x$-direction, one end of the O-ring is squeezed and one end is released slowly, the radial reaction force on the outer ring at the squeezed end increases, and the radial reaction force on the outer ring at the released end decreases, so that the outer ring is subjected to an increase in the total radial reaction force along the $x$-direction.

Fig. 4Displacement cloud diagram of O-ring damper

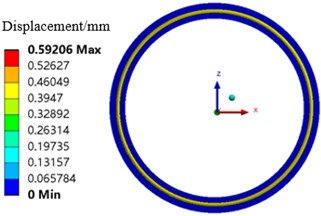
a) Displacement cloud after interference assembly

b) Compressed displacement cloud

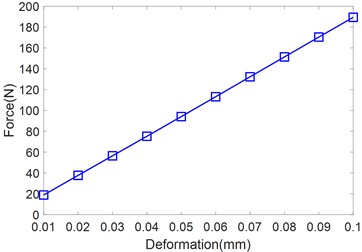
The radial reaction force of the O-ring on the outer ring during the extrusion process is calculated, and the difference between the neighboring loads and displacements is used to calculate the static stiffness of the O-ring in this system, and the results are shown in Fig. 5.

Fig. 5Stiffness characteristics of the O-ring under 0.29 mm compression

The stiffness equations are as follows:

11

$K_r=\frac{\mathrm{\Delta }F}{\mathrm{\Delta }X},$

where $\mathrm{\Delta }F$is the load difference between two neighboring measurement points; $\mathrm{\Delta }X$ is the displacement difference.

The results show that although the rubber material is a nonlinear material, the static load of the O-ring shows an approximately linear relationship with the change of displacement, and the stiffness magnitude is 1.8939×10⁶N/m. This is because the maximum gap between the inner and outer rings of the damper is only 0.11 mm, each time the displacement of the O-ring increases in 0.01 mm or so, until its displacement reaches 0.1 mm; and the interference fit leads to the O-ring in the initial moment there has been 0.29 mm of pre-compression, pre-compression makes the O-ring and the inner and outer rings of the damper between the contact pressure is greater. Therefore, the stiffness results show an approximately linear relationship.

3.1. Test program

In order to study the stiffness characteristics of O-rings, a static stiffness test rig for O-rings was designed and constructed, as shown in Fig. 6, and the main test equipment included: O-ring, force transducer, displacement transducer, damper inner and outer rings, etc. In this case, the squirrel cage elastic support is used as the damper outer ring, and the shaft as the inner ring. O-ring static stiffness determination is to simulate its working force in non-working condition. In the operating condition, the vibration of the journal is transmitted to the inner surface of the inner ring and the actual load is applied to the inner ring. During the test, in order to facilitate the test, a horizontal tension force is applied to the outer ring of the O-ring damper, and a displacement sensor is set up on the opposite side of the tension direction. After applying the force to the O-ring, its deformation under different static loads is measured, so as to determine its stiffness characteristics.

Fig. 6O-ring static stiffness test-bed

3.2. Analysis of test results

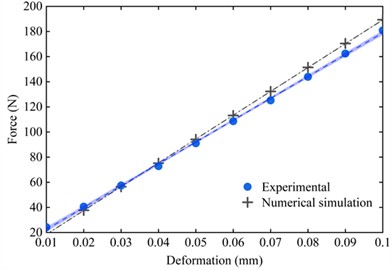
The O-ring static stiffness test results and simulation calculations are shown in Fig. 7. The overall trend of the simulation and experimental curves is consistent, and the experimental test static stiffness magnitude is 1.799×10⁶N/m. The error between the simulated and tested values is within 5.27 %. This proves the accuracy of the selection of the O-ring superelastic intrinsic model and the rationality of the finite element modeling method. The error between the simulation and the test comes from the assembly of the test piece and the machining error that makes the gap between the inner and outer rings deviate from the actual value.

4.1. Effect of precompression on static stiffness of O-rings

During engine operation, the proper amount of pre-compression will provide sufficient contact pressure between the O-ring and the inner and outer rings to realize the sealing effect while providing sufficient support stiffness. In this section, the effect of pre-compression on the static stiffness of O-rings is investigated by adjusting the outer ring size to change the amount of O-ring pre-compression. The relationship between the outer ring size and the amount of pre-compression is shown in Table 2.

The contact state of the O-ring without pre-compression is illustrated in Fig. 8(a). In this scenario, the cross-sectional diameter $d_1$ of the O-ring equals the distance $e_1$ from the groove bottom to the outer ring ($d_1=e_1$). After assembly, no contact pressure exists between the damper’s outer ring and the O-ring. Fig. 8(b). depicts the contact state under pre-compression. Here, the O-ring’s cross-sectional diameter $d_1$ exceeds the distance $e_1$ from the groove bottom to the outer ring ($d_1>e_1$). Following interference assembly, contact pressure develops between the outer ring and the O-ring, with both the contact width and pressure increasing as the outer ring compresses the O-ring.

Fig. 8Contact state between the O-ring and the outer ring of the damper with and without pre-compression

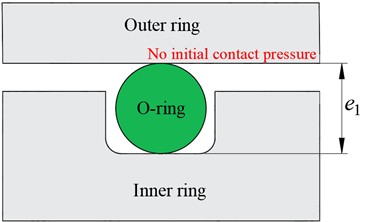
a) O-ring contact state without pre-compression

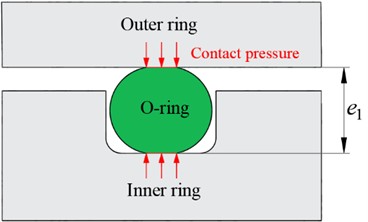
b) O-ring contact state with pre-compression

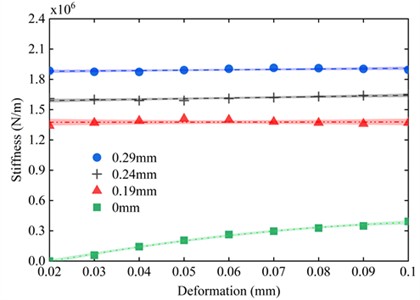
Fig. 9. shows the stiffness characteristics of the O-ring under different pre-compressions. From the stiffness change rule, in the pre-compression state, the O-ring stiffness curve basically maintains the linearity; while in the state without pre-compression, the O-ring stiffness increases continuously with the displacement increase, and shows obvious non-linear characteristics.

Fig. 9The variation curve of O-ring stiffness with displacement under different pre-compressions

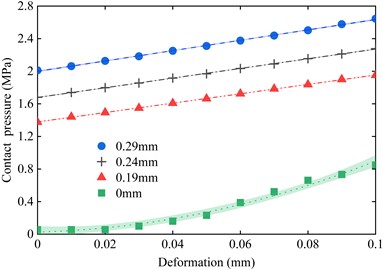
In order to analyze this phenomenon, the contact pressure (hereinafter referred to as “contact pressure”) of the entire O-ring before the start of loading with and without pre-compression was calculated, and the results are shown in Fig. 10. It can be found that when there is pre-compression (interference fit), contact pressure is generated where the O-ring contacts the inner and outer rings, and the maximum contact pressure is located at the centre of the contacting segment and decreases gradually to both sides, while when the pre-compression is 0 (no interference fit), there is no contact pressure. As the displacement of the O-ring increases, its contact pressure with the inner and outer rings increases, as shown in Fig. 11.

Fig. 10Initial contact pressure of the O-ring under different pre-compressions

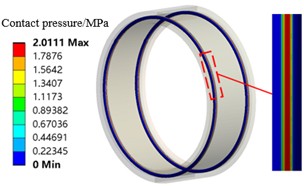
a) Pre-compression of 0.29 mm

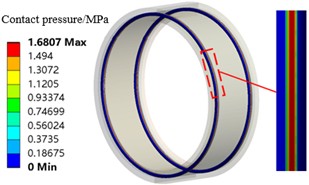
b) Pre-compression of 0.24 mm

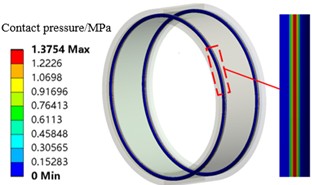
c) Pre-compression of 0.19 mm

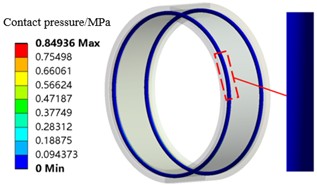
d) Pre-compression of 0 mm

Combining Fig. 10. and Fig. 11, it can be found that when there is precompression of the O-ring, the contact pressure increases linearly with the increase of displacement. 0.29 mm of precompression, the initial maximum contact pressure is 2.01 MPa, and when the displacement of the O-ring is increased by 0.01 mm, the contact pressure is only increased by about 0.1 MPa; when the displacement of the O-ring is increased to a maximum of 0.1 mm, the contact pressure is increased by a total of about 0.7 MPa. For the 0.24 mm and 0.19 mm pre-compressed states, similar results also occur. This indicates that the increase in contact pressure during compression of the O-ring is much smaller than the initial contact pressure, while the contact pressure increases linearly, and both of them together make the O-ring unable to show nonlinear characteristics. While the initial contact pressure is 0 when the O-ring is not pre-compressed, the contact pressure increases by a total of about 0.9 MPa as the displacement increases to 0.1 mm, and at the same time, the contact pressure increases nonlinearly with the increase of displacement, so that the O-ring exhibits an obvious nonlinear characteristic. In addition, the contact pressure increases as the amount of pre-compression increases, so the stiffness of the O-ring increases as the amount of pre-compression increases.

Fig. 11The contact pressure of O-ring changes with displacement under different pre-compression

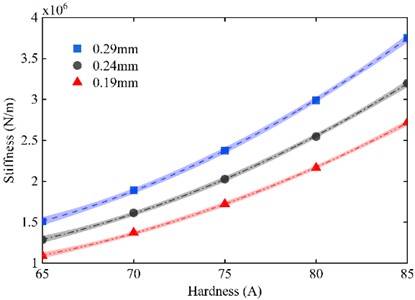
4.2. Effect of hardness on static stiffness of O-rings

Fluoroelastomers are highly stable and can withstand high temperatures, oil media, and a wide range of chemicals. And for the same fluoroelastomer material with different hardness, its material properties will be different. Keeping the structural dimensions of the O-rings unchanged, the static stiffness characteristics under the hardnesses of 65 A, 70 A, 75 A, 80 A, and 85 A were examined respectively, the hardness of the rubber material was changed, and the corresponding parameter values of the M-R model could be obtained according to Eq. (9) and Eq. (10), and the other constraints and loading conditions remained unchanged.

Fig. 12Changes of stiffness of three kinds of hardness O-rings with displacement without pre-compression

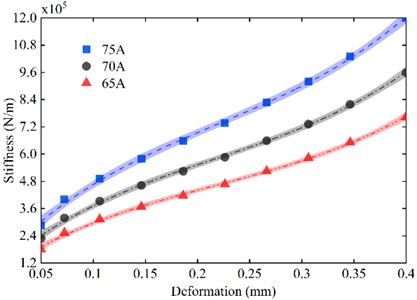
The simulation results for the influence of O-ring hardness on static stiffness under no pre-compression are shown in Fig. 12. As illustrated, the static stiffness of the O-ring increases with higher hardness under no pre-compression. This is attributed to the increased elastic modulus of the rubber material at greater hardness, which enhances its resistance to deformation, thereby elevating stiffness. Additionally, all three hardness levels of O-rings exhibit pronounced nonlinear characteristics in the absence of pre-compression.

Fig. 13. shows the curve of O-ring stiffness versus hardness with precompression. Similar to the case without pre-compression, the stiffness of the O-ring with pre-compression also increases with the increase of O-ring hardness. At 0.29 mm pre-compression, the hardness change from 65 A to 85 A increased the stiffness by 2.24×10⁶N/m. At 0.24 mm pre-compression, the stiffness increases by 1.91×10⁶N/m. The stiffness increased by 1.63×10⁶N/m at 0.19 mm of pre-compression. This means that the higher the pre-compression, the more the O-ring stiffness is affected by the hardness.

Fig. 13The variation curve of O-ring stiffness with hardness during pre-compression

4.3. Effect of temperature on static stiffness of O-rings

During engine operation, its temperature changes constantly, causing the temperature of the O-ring damper to change as well. Temperature changes will cause thermal deformation of the inner and outer rings of the damper, and at the same time, change the hardness of the O-ring. The rubber material properties are related to temperature as follows:

where $H_{rt}$ is the hardness of the material at ambient temperature $T$; $H_{rst}$ is the hardness of the material at standard room temperature; $T$ is the ambient temperature; $\beta$ is the temperature correction coefficient, and $\beta =$–0.13 is taken in the range of 70 A-75 A [23]. An increase in temperature leads to a decrease in the hardness of O-rings. The relationship between rubber hardness and temperature is described by Eq. (12). Based on the correlation between rubber hardness and elastic modulus in Eq. (10), the material parameters of O-rings under varying temperatures are derived and summarized in Table 3.

First, excluding the effect of temperature on the inner and outer rings of the damper, only the effect of temperature on the O-ring must be considered. Fig. 14. shows the results of the effect of operating temperature on the static stiffness of O-rings without pre-compression. From the fig, it can be seen that the static stiffness of the O-ring decreases with the increase in temperature, which is due to the decrease in the hardness of the O-ring caused by the increase in temperature [23], and the modulus of elasticity decreases, and the ability of the O-ring to resist deformation is reduced, thus the stiffness decreases. In addition, the stiffness of O-rings at different operating temperatures without pre-compression shows obvious non-linear characteristics.

Fig. 14The change of stiffness of O-ring with displacement at three temperatures without pre-compression

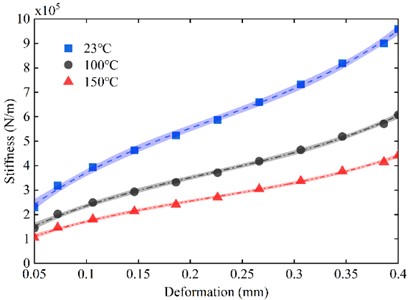
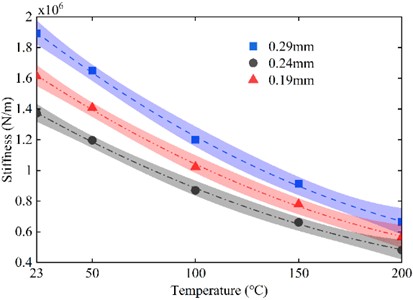
Fig. 15. shows the variation curve of O-ring stiffness with temperature during pre-compression. Similar to the case without pre-compression, the stiffness of O-rings with pre-compression similarly decreased with increasing temperature. The stiffness decreased by 1.23×10⁶ N/m for 0.29 mm of pre-compression, 1.05×10⁶N/m for 0.24 mm of pre-compression, and 0.89×10⁶N/m for 0.19mm of pre-compression for the range of temperature change from 23 ℃ to 200 ℃. It shows that the O-ring stiffness is more affected by temperature at higher pre-compression.

Fig. 15The change curve of O-ring stiffness with temperature during pre-compression

Secondly, the thermal deformation effects of the damper’s inner and outer rings under temperature variations are further considered. As temperature increases, the inner ring expands outward, enlarging the diameter of the groove base. In this study, the referenced engine structure features a fixed outer ring (structural schematic in Fig. 16(a)), where the outer ring contracts inward due to thermal expansion, reducing the squeeze clearance $c$, thereby increasing the pre-compression and contact pressure. For comparative analysis, the scenario of a freely expanding outer ring surface is also examined (structural schematic in Fig. 16(b)), where outward thermal expansion of the outer ring enlarges the squeeze clearance $c$, leading to reduced pre-compression and contact pressure. The clearance variations of the damper under different temperatures are listed in Table 4, where $c_1=$0.11 mm, represents the initial clearance before deformation, and $c_2$ denotes the post-deformation clearance.

Fig. 16Effect of temperature on damper structure at different

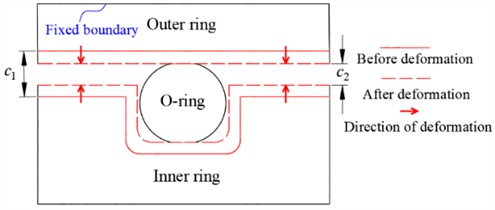
a) Outer ring fixation

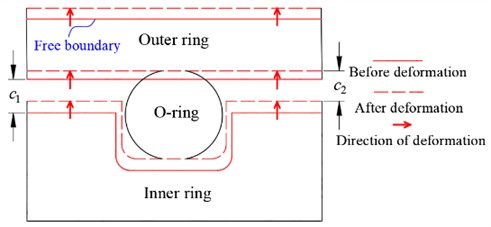
b) Outer ring freedom

After coupling the thermal deformation of the inner and outer rings of the damper with the change in the hardness of the O-ring, the effect of temperature on the static stiffness of the O-ring under pre compression of 0.29 mm is shown in Fig. 17.

Fig. 17Variation curve of static stiffness of O-ring with temperature considering deformation of inner and outer rings

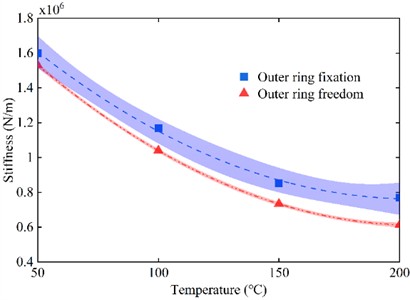
In both cases, the static stiffness of the O-ring gradually decreases with the increase of temperature and the trend of change gradually slows down. The higher the temperature, the smaller the effect of temperature on the static stiffness of the O-ring. When the outer ring is fixed, the gap is smaller than when the outer ring is free, and the contact pressure is greater, so the static stiffness of the O-ring is greater. And as the temperature increases, the difference in static stiffness between the two cases increases from 4.4 % to 20.4 %.