Abstract
In the steering system, the vibration generated by the steering gear can seriously affect human driving comfort, and effective vibration reduction is crucial. Acoustic black hole (ABH) is a vibration reduction and noise reduction technology that controls the consumption and aggregation of bending waves through thin-walled power function structure changes. A design scheme of embedding a 2D ABH plate in the steering column is proposed to address the vibration reduction issue of the steering gear. Using the finite element method, the natural frequency and velocity response curve of the steering gear is obtained. Then we embed a 2D ABH into the steering gear model. The steering gear model embedded with 2D ABH was subjected to finite element analysis to obtain the vibration characteristics and velocity response and acceleration curve of the steering gear after adding 2D ABH. The results indicate that the vibration velocity and acceleration of the steering gear embedded with ABH is lower throughout the entire frequency range. The maximum damping is around 510 Hz, and the minimum damping is around 294 Hz.
1. Introduction
Acoustic black hole (ABH), as an emerging technology in the field of wave manipulation, has the characteristics of lightweight, high integration, and strong constructability. It is a new passive noise and vibration reduction technology with broad application prospects. Pekeris [1] first discovered that when sound waves propagate in a special non-uniform medium, their velocity decreases as the thickness of the medium decreases, and the sound waves do not reflect. This phenomenon is called the acoustic black hole phenomenon. Mironov[2] first proposed the ABH structure, which means that when the thickness of the ABH structure varies in the form of a power function (the power exponent is not less than 2), the wave velocity of the bending wave will decrease as the thickness of the structure decreases. Ideally, the wave velocity can be reduced to zero. Krylov [3-5] derived a power function expression for the thickness of wedge-shaped structures using geometric acoustic methods and was the first to apply ABH structures to 1D beam structures. Experimental results have shown that adding a layer of damping material at the ABH region can effectively suppress the reflection of sound waves and improve the performance of ABH structures.
At present, the application research of ABH structure is very extensive. Liu [6] replaced perfect ideal ABH with imperfect ABH and calculated the radiation efficiency of imperfect ABH through the finite element method, verifying that the acoustic radiation efficiency can be controlled by imperfect ABH. Zhen [7]proposed ABH combining APPN (active-passive hybrid piezoelectric network) to obtain the vibration modes of ABH plates through the finite element method and verified that the new system combining APPN and ABH can effectively control vibration and reduce noise. Wen [8], [9] applied ABH to dynamic absorbers and reinforced structures, effectively achieving better vibration reduction effects. Ma [10] applied the ABH effect to the problem of heavy flow and analyzed it by transmitting sound radiation to an ABH plate in water, verifying that ABH has vibration reduction and noise reduction effects in heavy fluids. Du [11] optimized the ABH model and verified that the optimized ABH vibration reduction effect was significantly improved by combining the surrogate model with the finite element method. Humbert[12] applied ABH to 3D-print lightweight structures, effectively suppressing vibrations. Bao [13] proposed the dynamic performance problem of the ABH array and verified through finite element and experimental methods that the ABH array effectively increases the structural modal density and loss factor.
From this, it can be seen that research on the application of ABH is currently very popular. At the same time, it indicates that the application of ABH in the field of vibration reduction and noise reduction research has great potential. But, their application in the field of automotive engineering is still limited. The automotive steering gear is an important component in the automotive steering system. And the vibration and noise of the car steering system have a significant impact on driving comfort. Therefore, this paper proposes a design scheme for embedding a 2D ABH plate in the SUV steering gear. The natural frequency and velocity response curves of the steering gear and the embedded 2D ABH steering gear were obtained by finite element simulation method. The suppression effect of 2D ABH on the vibration of steering gears is confirmed through analysis and comparison.
2. Modeling of vibration characteristics simulation and analysis results
2.1. ABH principle
ABH are structures whose thickness varies in a specific direction according to a power function, which can achieve overall structural vibration and noise reduction by concentrating bending waves in the structure. ABH can be divided into one-dimensional and 2D ABH, as shown in Fig. 1. The 1D ABH structure is wedge-shaped and the thickness of its cross-section smoothly decreases to zero according to a power function curve. The relationship between the local thickness of the wedge-shaped block and the distance from that location to the edge of the wedge-shaped block can be expressed as:
where, is the proportionality coefficient; is a power function exponent that must satisfy 2; is the radius of the 2D ABH region; is the cutoff thickness of the ABH, which is the distance between the center of the acoustic black hole and the bottom of the plate.
A 2D ABH is obtained by rotating the tip of 1D ABH as the center, and its shape presents a downward concave circular structure. This structure achieves noise reduction by controlling the power function variation of its thickness to control bending waves. Compared to 1D ABH, 2D ABH structures have better structural stability due to their circular shape and uniform thickness variations. Its unique structural design and acoustic localization effect can achieve higher noise reduction efficiency.
Fig. 1ABH structure
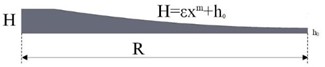
a) 1D ABH structure

b) 2D ABH structure
2.2. Establishment of finite element model
Simplify the model based on the complete three-dimensional model of the steering gear. Mainly focused on: removing some features that have little impact on the structure, for more complex components (steering gear housing), then a remodeling was carried out to ensure high precision in key geometric dimensions such as inner and outer diameters, length, offset angle, as well as platform position dimensions for installation and fixation. Then assemble the reconstructed large shell model of the steering gear with the simplified models of other components to obtain the overall 3D model of the steering gear, as shown in Fig. 2. The simplified assembly model consists of 21 components.
Fig. 2Steering gear model

a) 2 Simplified 3D model of steering gear

b) Internal structure of 3D model of steering gear
The steering gear model is established by 3D software. The thickness of the ABH region satisfies Eq. (1), where the 2D ABH parameters ε, m, and R take values of 0.00125, 2, and 60 mm, respectively. The large outer shell of the steering gear has complex features such as intersecting cylinders. It is necessary to first cut the large outer shell of the steering gear. The mesh size of the intersecting cylinders of the large outer shell is 2 mm, and the area with large curvature is encrypted. The minimum mesh size during encryption is 0.4 mm, and the characteristic angle is 30°. For other parts of the large outer shell of the steering gear, the mesh size is set to 5 mm, and the area with large curvature is encrypted. The minimum mesh size during encryption is 0.8 mm, and the characteristic angle is 30°. The finite element model of the steering gear is divided into 521036 units as shown in Fig. 3(a). The grid processing method for embedding the 2D ABH steering gear is consistent with that without adding it. The finite element model of embedding the 2D ABH is divided into 609329 grid elements as shown in Fig. 3(b). The structural parameters of the steering gear and 2D ABH are shown in Table 1.
Fig. 3Finite element model

a) Finite element model of steering gear
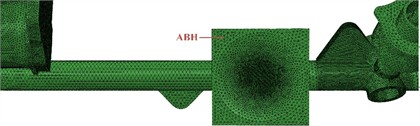
b) Finite element model of steering gear and ABH
Table 1Material attribute table
Material | / (kg·m-3) | / Pa | Damping | |
Fe | 7.8e3 | 2.1e11 | 0.3 | 0.005 |
Al | 2.7e3 | 6.9e10 | 0.33 | 0.005 |
Subsequently, the grid partition file is imported into finite element software. The fixed position is a small area on the surface of the installation platform, as shown in Fig. 4(a), with three degrees of freedom of limited to the fixed position. The steering gear model is subjected to modal analysis to obtain the modal characteristics of the steering gear and the embedded two-dimensional acoustic black hole, and the results are imported into the vibration response module. A force of 100 N is applied to the left screw of the steering gear in the direction of , as shown in Fig. 4(b), and the vibration response analysis conditions are set to 0-1000 Hz.
Fig. 4Vibration response constraint diagram

a) Constraint diagram

b) Incentive point diagram
2.3. Result analysis
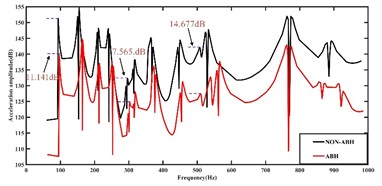
Table 2 shows the first 6 natural frequencies of the steering gear obtained from modal analysis. From Table 2, it can be seen that compared to the original structure, the steering gear with embedded ABH has an increase in the natural frequency of each order, but the change is not significant. In vibration response analysis, the reference velocity and vibration velocity units are set to 0.01 m.s-1 and dB. Fig. 5 shows the detection point, where the extracted vibration acceleration and velocity results will be compared. Fig. 6 shows a comparison of vibration response results, including velocity and acceleration results. Fig. 6(a): Comparison of Vibration Response of ABH Steering Gear. Due to the increase in natural frequency after embedding ABH, the velocity response curve of the embedded ABH shifts to the right. The number of vibration peaks in the steering gear is relatively high between 0 and 300 Hz, and the addition of ABH in the entire frequency range results in lower vibration velocity. At the highest peak, the vibration velocity decreases by 10.80 dB. When the frequency is around 510 Hz, the vibration velocity is reduced by a maximum of 15.16 db, and when the frequency is around 294 Hz, the vibration velocity is reduced by a minimum of 7.63 db. Fig. 6(b) shows the acceleration diagram of a silent black hole steering gear. At the peak, the vibration velocity decreases by 11.141 dB. When the frequency is around 510 Hz, the maximum decreases is 14.382 dB, and when the frequency is around 294 Hz, the minimum decreases is 7.565 dB. It indicates that after embedding the 2D ABH, the vibration velocity of the steering gear decreases and the embedding of the 2D ABH can achieve a good vibration reduction effect.
Table 2Comparison of natural frequency of ABH steering gear
Degree (Hz) | First | Second | Third | Fourth | Fifth | Sixth |
NON-ABH | 91.741 | 153.46 | 153.87 | 187.69 | 209.91 | 241.84 |
ABH | 94.852 | 160.49 | 164.48 | 193.97 | 212.89 | 252.88 |
Fig. 5Result detection points
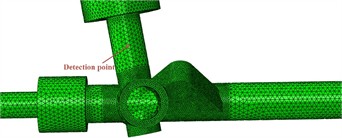
Fig. 6Vibration response results
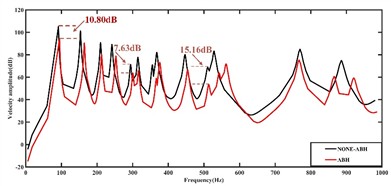
a) Vibration response speed result chart
b) Vibration response acceleration result chart
3. Conclusions
To reduce the vibration of automobile steering gear, this study proposes a vibration control design scheme by embedding an ABH structure in the steering gear. The natural frequency and vibration response of the steering gear and 2D ABH steering gear models were solved by finite element simulation. Finally, the impact of ABH parameters on the vibration suppression effect of the steering gear is discussed. The main research results are as follows:
1) According to the modal analysis results, the natural frequency of the steering gear with and without the addition of a 2D ABH does not change significantly, so it will not cause vibration of the steering gear at the new frequency.
2) Compared with the frequency response curve of the silent black hole steering gear, the overall curve of the steering gear decreases after embedding the acoustic black hole. It is found that the maximum decrease is 15.16 dB near the frequency of 510 Hz, and the minimum decrease is 7.63 dB at the frequency of 294 Hz. Compared with the acceleration curve of the silent black hole steering gear, the vibration velocity at the peak decreases by 11.141 dB, the maximum decrease is 14.382 dB when the frequency is around 510 Hz, and the minimum decrease is 7.565 dB when the frequency is around 294 Hz. It is concluded that adding a 2D ABH has an effect on reducing vibration in the steering gear.
References
-
C. L. Pekeris, “Theory of propagation of sound in a half-space of variable sound velocity under conditions of formation of a shadow zone,” The Journal of the Acoustical Society of America, Vol. 18, No. 2, pp. 295–315, Oct. 1946, https://doi.org/10.1121/1.1916366
-
M. A. Mironov, “Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval,” Soviet Physics-Acoustics, Vol. 34, No. 1, pp. 318–319, 1988.
-
V. V. Krylov, “New type of vibration dampers utilizing the effect of acoustic ‘black holes’,” Acta Acustica United with Acustica, Vol. 90, No. 5, pp. 830–837, 2004.
-
V. V. Krylov, “Geometrical-acoustics approach to the description of localized vibrational modes of an elastic solid wedge,” American Institute of Physics, Vol. 25, No. 2, pp. 137–140, 1990.
-
V. V. Krylov, “Overview of localised flexural waves in wedges of power-law profile and comments on their relationship with the acoustic black hole effect,” Journal of Sound and Vibration, Vol. 468, p. 115100, Mar. 2020, https://doi.org/10.1016/j.jsv.2019.115100
-
P. C. Liu, Y. Q. Zhou, and R. Li, “Low-frequency sound radiation characteristics of an imperfect acoustic black hole in thin plate,” Journal of Low Frequency Noise, Vibration and Active Control, Vol. 42, No. 3, pp. 985–996, 2023.
-
Y. Zhen, H. Li, and Y. Tang, “Novel vibration control method of acoustic black hole plates using active-passive piezoelectric networks,” Thin-Walled Structures, Vol. 186, p. 110705, May 2023, https://doi.org/10.1016/j.tws.2023.110705
-
H. Wen, X. Guo, R. Ma, J. Guo, Z. Shi, and L. Ye, “Vibration control mechanisms of plate structures by 1D acoustic black hole dynamic vibration absorber,” Physica Scripta, Vol. 99, No. 5, p. 055268, May 2024, https://doi.org/10.1088/1402-4896/ad3e39
-
H. Wen, J. Jiang, H. Huang, J. Guo, and L. Ye, “Acoustic characteristics of composite structures with 2D acoustic black holes and stiffened plates,” Applied Acoustics, Vol. 216, p. 109805, Jan. 2024, https://doi.org/10.1016/j.apacoust.2023.109805
-
L. Ma and L. Cheng, “Vibration and sound radiation of an acoustic black hole plate immersed in heavy fluid,” The Journal of the Acoustical Society of America, Vol. 154, No. 1, pp. 179–190, Jul. 2023, https://doi.org/10.1121/10.0020067
-
X. Du and Q. Fu, “Surrogate model-based multi-objective design optimization of vibration suppression effect of acoustic black holes and damping materials on a rectangular plate,” Applied Acoustics, Vol. 217, p. 109837, Feb. 2024, https://doi.org/10.1016/j.apacoust.2023.109837
-
C. Humbert, H. Monthoil, and P. Nicolay, “Passive mitigation of low-frequency vibration modes in lightweight structures based on a new generation of acoustic black holes,” Engineering Research Express, Vol. 6, No. 1, p. 015049, Mar. 2024, https://doi.org/10.1088/2631-8695/ad176a
-
Y. Bao, X. Liu, Z. Yao, Y. Shan, and T. He, “Vibration energy accumulation and absorption characteristics of pseudo acoustic black hole wedge,” Mechanics of Advanced Materials and Structures, Vol. 31, No. 18, pp. 4309–4324, Sep. 2024, https://doi.org/10.1080/15376494.2023.2193976
About this article
This research was funded by the National Natural Science Foundation of China (52405275), Natural Science Foundation of the Higher Education Institutions of Jiangsu Province, China (24KJB460017) and the Scientific Research Foundation for High-Level Talents of Nanjing Institute of Technology (YKJ202102).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
