Multi-mode frequency response prediction of milling robot based on feature transferring with small sample sets

1. Introduction

Six‐degree‐of‐freedom (6‐DOF) industrial robots are increasingly employed in milling operations because they offer lower cost, higher efficiency, greater flexibility, and a larger workspace [1–3]. However, their comparatively low structural stiffness – only 1/50 to 1/20 of that of conventional CNC machine tools – combined with the high periodic cutting forces generated during milling, makes robotic machining highly susceptible to forced vibrations and chatter [4]. Chatter not only degrades surface quality but can also lead to premature tool wear or even structural damage to the robot itself [5]. Moreover, a robot’s stiffness and dynamic behavior change with its posture [6], so accurately predicting its dynamic response across different configurations is essential for suppressing chatter and ensuring machining precision.

One of the most common ways to mitigate chatter is to predict the stability region via stability lobe diagrams (SLDs). Since Tlusty and Tobias introduced analytical stability equations [7, 8], various methods for SLD prediction have been proposed [5, 9-12]. A critical input to all these methods is the frequency response function (FRF) of the machining system. In practice, the FRF is usually obtained through impact testing, but impact testing can only capture the system’s FRF at a fixed posture. It cannot measure the tool‐tip FRF dynamically during real‐time machining – which is precisely the most critical point for predicting chatter. In robotic milling, the robot must continuously change posture to follow complex workpiece geometries, so the tool‐tip dynamics vary throughout the process. Consequently, a predictive model that can estimate the milling robot’s FRF under arbitrary postures is crucial for maintaining process stability and high‐quality machining.

Analytical modeling techniques have been developed to estimate a robot’s dynamic properties by characterizing link and joint dynamics [13-17]. While these models can, in principle, predict how a robot’s dynamics change with configuration [18-19], they struggle to account for uncertainties in joint stiffness, damping, and inertia. Sources of these uncertainties include gear backlash, nonuniform mass distribution in the links, and manufacturing variability [20]. Furthermore, stiffness and damping characteristics depend heavily on the specific robot model and the end‐effector tool, making it difficult to create a comprehensive map of dynamic properties across the entire workspace [21-23]. For instance, Huynh et al. [24] combined rigid‐body identification with experimental modal analysis to determine a robot’s inertial, stiffness, and damping parameters. Despite improvements that allowed them to capture modes involving joint deflection about axes perpendicular to the rotation axis, the overall parameter identification process remained complex and time‐consuming.

To address these challenges, Nguyen et al. [20] proposed a statistical approach using Gaussian process regression (GPR) to model a 6‐DOF robot’s dynamics within its workspace. By sampling modal parameters from impact tests at discrete locations and training a GPR model, they could predict modal parameters at untested locations. However, their method requires a large number of training samples, and prediction accuracy deteriorates in sparsely sampled regions – especially further from the robot base. Moreover, it considers only first‐order modal characteristics. In high‐speed milling, increasing spindle speeds excite higher‐order FRFs in multi‐degree‐of‐freedom (M‐DOF) systems. As a typical M‐DOF system, a milling robot’s higher‐order modes become significant at elevated cutting speeds, so methods that neglect multi‐mode FRFs are insufficient for high‐speed robotic milling. Therefore, there is a clear need for an accurate, efficient approach to predict multi‐mode FRFs in milling robots.

This study proposes a novel feature‐transfer-based method to predict multi‐mode FRFs for milling robots, while overcoming the drawbacks of existing approaches – namely, extensive experimentation, complex computations, and long processing times. Instead of identifying joint‐space stiffness and inertia parameters, the proposed method requires only a small number of impact tests to build sample sets. First, impact tests are performed at selected points on the robot body under both a “source” posture and a “target” posture. The measured FRFs are organized into second‐order complex tensors, facilitating the transfer of FRF features between the two postures. Next, the multi‐mode parameters of the tool‐tip FRF under the source posture are extracted using the least‐squares complex exponential (LSCE) method and assembled into a label vector. A complex‐kernel extreme learning machine with augmented inputs (CKELM‐AI) is then trained to predict the tool‐tip multi‐mode FRF under the target posture. To improve prediction accuracy, a CKELM‐AI – based virtual sample generation strategy is introduced, and feature augmentation – including statistical, frequency, and time–frequency features – is applied. The remainder of this paper is organized as follows: Section 2 presents the underlying theories and methods; Section 3 details the feature‐transfer–based algorithms for FRF prediction; Section 4 outlines the multi-mode FRF prediction workflow; Section 5 provides a comprehensive case study to validate the method; and Section 6 summarizes the conclusions and discusses future work.

2. Preliminaries

2.1. Extreme learning machine

The extreme learning machine (ELM) was originally developed based on single hidden layer feedforward networks (SLFNs) [25], as illustrated in Fig. 1.

Fig. 1Architecture of the ELM

For $N$ arbitrary samples $\{\left({\mathbf{x}}_i,{\mathbf{t}}_i\right){\}}_{i=1}^N$, an SLFN with $m$ hidden nodes can be expressed as:

1

${\mathbf{y}}_i={\sum }_{p=1}^m{\beta }_{p}g\left({\mathbf{\omega }}_p{\mathbf{x}}_i+b_p\right)\begin{array}{cc},& i=\mathrm{1,2},\cdots ,N,\end{array}$

where ${\mathbf{\omega }}_p$ represents the input weight vector connecting the input nodes to the $p\text{th}$hidden node, $b_p$ denotes the threshold (bias) of the $p$th hidden node, and ${\beta }_p$ is the output weight vector linking the $p\text{th}$ hidden node to the output nodes.

That SLFNs can approximate these $N$ samples with zero error, which means that there exist ${\mathbf{\omega }}_p$, $b_p$ and ${\beta }_p$ such that:

2

${\mathbf{t}}_i={\sum }_{p=1}^m{\beta }_{p}g\left({\mathbf{\omega }}_p{\mathbf{x}}_i+b_p\right)\begin{array}{cc},& i=\mathrm{1,2},\cdots ,N\end{array},$

which can be rewritten as:

3

$\mathbf{T}=\mathbf{H}\mathbf{\beta },$

where $\mathbf{H}$ is the hidden layer output matrix, $\mathbf{\beta }$ is the output weight vector, $\mathbf{T}$ is the target vector.

In the training process, the input weights ${\mathbf{\omega }}_p$ and threshold $b_p$ are randomly generated and assigned. And in most case, the number of samples $N$ and hidden nodes $m$ is not equal, thus the least square method can be utilized to solve Eq. (3) analytically:

4

$\mathbf{\beta }={\mathbf{H}}^{†}\mathbf{T},$

where ${\mathbf{H}}^{†}$ denotes the Moore-Penrose generalized inverse of $\mathbf{H}$.

3. Methodologies

3.1. Complex kernel extreme learning machine with augmented input

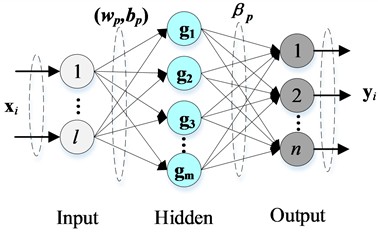
The kernel extreme learning machine (KELM) is an enhanced version of the extreme learning machine (ELM) that incorporates a kernel function [32]. This allows feature mappings to include both random hidden nodes and kernels. KELM can preserve a specific mapping using a kernel function, independent of the mapping correlation, and reduces both training error and output weight error, thereby improving learning efficiency, accuracy, generalization, and stability. To address the FRF prediction problem for milling robots, where sample features are complex, a complex kernel learning machine with augmented input CKELMAI is developed in this study, inspired by the augmented complex-valued extreme learning machine developed in [33], as shown in Fig. 2.

Fig. 2Architecture of the CKELMAI

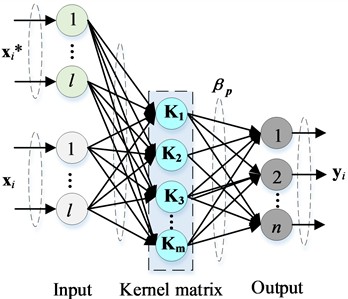
In CKELMAI, the output weight $\mathbf{\beta }$ is calculated by introducing the coefficient $C$ and the diagonal of $\mathbf{H}{\mathbf{H}}^H$, as follows:

7

$\mathbf{\beta }={\mathbf{H}}^H{\left(\frac{1}{C}+\mathbf{H}{\mathbf{H}}^H\right)}^{-1}\mathbf{T}.$

To address the issue of acquiring second-order statistics in complex domain learning, the conjugate information of the input sample ${\mathbf{x}}_i$ is incorporated into the original input as an augmented input. This can be mathematically expressed as:

8

${\mathbf{x}}_i^a={\left[{\mathbf{x}}_i,{\mathbf{x}}_i^{*}\right]}^T\in {\mathbb{C}}^{2l},$

where ${\left(\cdot \right)}_{}^{*}$ denotes complex conjugate and $l$ is the length of the sample ${\mathbf{x}}_i$.

At this point, the output function corresponding to the regularized ELM is expressed as:

9

${\mathbf{y}}_i={\sum }_{p=1}^m\mathbf{h}\left({\mathbf{x}}_i^a\right){\mathbf{H}}^H{\left(\frac{1}{C}+\mathbf{H}{\mathbf{H}}^H\right)}^{-1}\mathbf{T}\begin{array}{cc},& i=\mathrm{1,2},\cdots ,N\end{array}.$

Furthermore, the output function of CKELMAI can be written as:

10

${\mathbf{y}}_i={\sum }_{p=1}^m{\left[\begin{array}{c}K\left({\mathbf{x}}_{}^a,{\mathbf{x}}_1^a\right)\\ \cdots \\ K\left({\mathbf{x}}_{}^a,{\mathbf{x}}_N^a\right)\end{array}\right]}^H{\left(\frac{1}{C}+{\mathrm{\Omega }}_{KELM}\right)}^{-1}\mathbf{T}\begin{array}{cc},& i=\mathrm{1,2},\cdots ,N\end{array},$

where ${\mathrm{\Omega }}_{KELM}=\left\{{\mathrm{\Omega }}_{i,j}\right\}$ and ${\mathrm{\Omega }}_{i,j}=K\left({\mathbf{x}}_i^a,{\mathbf{x}}_j^a\right)$ denote the kernel function, the complex Gaussian kernel is utilized in this study:

11

$\mathbf{K}\left({\mathbf{x}}_i^a,{\mathbf{x}}_j^a\right)=\exp \left(-\frac{{\left({\mathbf{x}}_i^a-{\mathbf{x}}_j^a\right)}^H\left({\mathbf{x}}_i^a-{\mathbf{x}}_j^a\right)}{\gamma }\right),$

where $\gamma$ is kernel parameter utilized to control the width of the sample Gaussian distribution.

3.2. CKELMAI-enabled complex virtual sample generation

The PSO-based visual sample generation method [30] has been widely applied in generating visual samples in real domains. However, it is not directly applicable to virtual sample generation in the complex domain due to inherent limitations in its generation mechanism. To address this issue, this study introduces targeted improvements and optimizations tailored to the generation of virtual samples in the complex domain for FRF prediction.

3.2.1. Complex acceptable domain range expansion

In this study, a double-triangular membership-based complex information-expanded (DMCIE) function is introduced to asymmetrically extend the complex domain range of each feature, as illustrated in Fig. 3.

Fig. 3Schematic of double-triangular membership-based complex information-expanded function

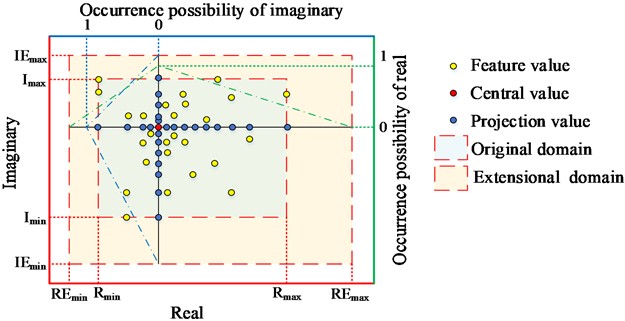
In this figure, the actual values of the original features $q_{\epsilon }$ ($\epsilon =1,...,E$, $E$ denotes the total number of features in a sample) are represented by yellow dots. The projections of these original feature values onto the real and complex domains are indicated by blue dots, with the center of the original feature values shown as a red dot. The lower and right axes represent the real values and their occurrence probability, while the left and upper axes represent the imaginary values and their occurrence probability. The double-triangular region, drawn with a dot-dash line, represents the occurrence probability of the real or imaginary parts of the feature values. This visual representation allows for an intuitive understanding of the skewness of the DMCIE function, which depends on the distribution of the samples on both sides of the central value. The skewness values for the left, right, upper, and lower regions can be expressed as functions of the sample distribution, as follows:

12

$S{K}_{Left}=\frac{N_{Lreal}}{N_{Lreal}+N_{Ureal}+SP},$
$S{K}_{Right}=\frac{N_{Ureal}}{N_{Lreal}+N_{Ureal}+SP},$
$S{K}_{Upper}=\frac{N_{Limag}}{N_{Limag}+N_{Uimag}+SP},$
$S{K}_{Lower}=\frac{N_{Uimag}}{N_{Limag}+N_{Uimag}+SP},$

where $N_{Lreal}$, $N_{Ureal}$, $N_{Limag}$ and $N_{Uimag}$ represent the number of samples smaller or greater than the center value of the feature along the left, right, upper, and lower sides, respectively, among all samples. $SP$ is an adjusting parameter used to extend the acceptable domain range. At this point, the boundaries of the acceptable domain can be expressed as:

13

$R{E}_{min}=real\left(CV\right)-\frac{1}{S{K}_{Left}}\left(real\left(CV\right)-R_{min}\right),$
$R{E}_{max}=real\left(CV\right)+\frac{1}{S{K}_{Right}}\left(R_{max}-real\left(CV\right)\right),$
$I{E}_{min}=imag\left(CV\right)-\frac{1}{S{K}_{Lower}}\left(imag\left(CV\right)-I_{min}\right),$
$I{E}_{max}=imag\left(CV\right)+\frac{1}{S{K}_{Upper}}\left(I_{max}-imag\left(CV\right)\right),$

where $R_{min}$, $R_{max}$, $I_{min}$ and $I_{max}$ denote the minimum or maximum value of real or imaginary component on this feature among all the original samples, $CV$ is the center value of this feature among all samples, taking feature $q_{\epsilon }$ as an example:

14

$CV=\frac{1}{N}{\sum }_{i=1}^N{q}_{\epsilon }\left(i\right),$

where $N$ represents the total number of original samples.

3.2.2. Complex virtual sample generation

The implementation procedure of the PSO-based visual sample generation method has been described in Section 2.2. In this study, the original method is adapted to meet the requirements of multi-mode FRF prediction for milling robots.

Firstly, the number of outputs in the multi-mode FRF prediction problem exceeds one, and the importance of each output varies. For example, in the robotic milling process, higher mode orders typically have less importance, and the importance of the natural frequency is greater than that of the damping ratio. Therefore, for the testing set ${\mathbf{D}}_{test}=\left(\mathbf{x},\mathbf{t}\right)$, $\mathbf{t}=\left[t_1,\cdots ,t_n\right]$, the MAPE (used as the fitness function in optimization) should be expressed as:

15

$MAPE={\sum }_{q=1}^n{w}_q\left|\frac{t_q-{\widehat{t}}_q}{t_q}\right|,$

where $w_q$ is the weight of the $q$th output, representing its importance, and ${\sum }_{q=1}^n{w}_q=1$.

Secondly, since multi-mode FRF prediction is a problem in the complex domain, the TMIE-based asymmetric acceptable domain range expansion method is no longer applicable, and traditional ELM is insufficient to solve the prediction task. As a result, it would be impossible to control the MAPE to be less than 10 %. Therefore, the CKELMAI and DMCIE methods developed in Sections 3.1 and 3.2.1 are employed for the generation and filtering of complex visual samples.

The improved procedure is as follows:

(1) Dataset Partitioning: The original training set ${\mathbf{D}}_{original}=\{\left({\mathbf{x}}_i,{\mathbf{t}}_i\right){\}}_{i=1}^N$ is randomly divided into training subsets and testing subsets ${\mathbf{D}}_{test}=\{\left({\mathbf{x}}_i,{\mathbf{t}}_i\right){\}}_{i=1}^{Ntest}$. Weights ${\mathbf{D}}_{train}=\{\left({\mathbf{x}}_i,{\mathbf{t}}_i\right){\}}_{i=1}^{Ntrain}$$w_q$ in Eq. (15) are specified according to the actual requirements.

(2) Initial Forecasting Model Construction: Using ${\mathbf{D}}_{train}$ and ${\mathbf{D}}_{test}$, a forecasting model $\widehat{\mathbf{H}}$ is obtained by CKELMAI. The MAPE of the output is calculated using Eq. (15), ensuring it is kept below 10 % by optimizing the parameters $\gamma$ and $C$ in CKELMAI, where the methods described in reference [32] can be applied.

(3) Virtual Sample Initialization: The asymmetric acceptable domain range for each feature is calculated using DMCIE. $N_{vir}$ virtual input samples ${\mathbf{x}}_{vir,i}$ are then randomly generated within this range, and the outputs of these virtual samples ${\mathbf{t}}_{vir,i}$ are obtained using the original forecasting model $\widehat{\mathbf{H}}$. The combined dataset ${\mathbf{D}}_{vir}={\left\{\left({\mathbf{x}}_{vir,i},{\mathbf{t}}_{vir,i}\right)\right\}}_{i=1}^{Nvir}$ forms the initial set of virtual samples.

(4) Model Validation and Fitness Evaluation: $N_{vir}$ new forecasting models ${\widehat{\mathbf{H}}}_{new,i}$ are obtained by CKELMAI, trained on new training subsets composed of ${\mathbf{D}}_{train}$ and $\left({\mathbf{x}}_{vir,i},{\mathbf{t}}_{vir,i}\right)$. The predicted output values are obtained by testing ${\widehat{\mathbf{H}}}_{new,i}$ on ${\mathbf{D}}_{test}$, and the MAPE (fitness) of the virtual samples must be constrained to less than 10 % to ensure their validity.

(5) Optimization via PSO: PSO is used to repeat step (4) until convergence conditions are met. At this point, a virtual sample is generated within the acceptable prediction region. Steps (1) to (5) are then repeated until the desired number of virtual samples is obtained.

4. Multi-mode FRF prediction for milling robot

The framework of the developed multi-mode FRF prediction method for milling robots, based on feature transfer with small sample sets, is described in this section, as shown in Fig. 4.

1) Impact Testing and Data Collection: First, $n$ points on the robot body and one point on the tool tip under any two postures are selected for impact testing to obtain FRF data as the transferring source. Impact testing is also carried out on the points of the robot body under the target posture to acquire FRF data as the transferring target.

2) Constructing Complex Tensors and Identifying Parameters: The FRF data of the impact points on the robot body under both source and target postures are used to construct second-order complex tensors for the FRF features in the source and target domains, respectively. Multi-mode parameters of the FRF at the tool tip are identified using LSCE method, and these parameters are then organized into label vectors for the transferring source domain, as shown in Fig. 5.

Fig. 4The framework of multi-mode milling robot FRF prediction method

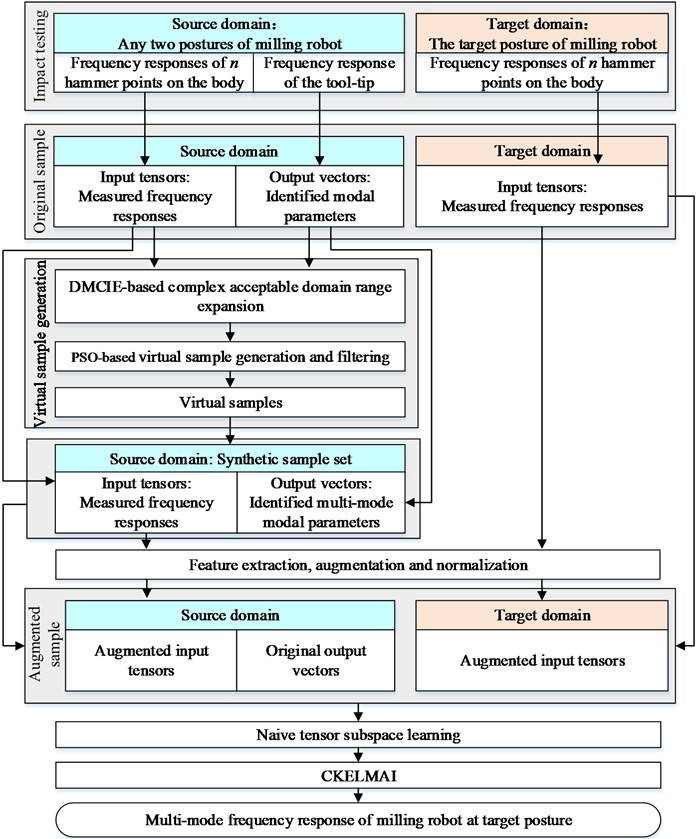
3) Virtual Sample Generation: Based on the input tensor and output vector from the transferring source domain, the CKELMAI-enabled complex virtual sample generation method developed in Section 3.2 is applied to generate virtual samples.

4) Feature Augmentation and Preprocessing: The feature augmentation method described in Section 3.3 is used to extract features in the frequency domain, time domain, and time-frequency domain. These extracted features are then added to the original FRF data as augmented features. A normalization method is applied to preprocess the augmented feature data to eliminate the impact of magnitude order on regression learning.

5) Tensor Dimension Reduction: The shared invariant subspace between the complex tensors in the source and target domains is obtained using the naive tensor subspace learning method described in Section 2.3, which helps reduce the tensor dimensions effectively.

6) FRF Prediction: Finally, the CKELMAI method developed in Section 3.1 is used to predict the multi-mode FRF of the tool tip under the target posture.

Fig. 5Sample representation for FRF prediction

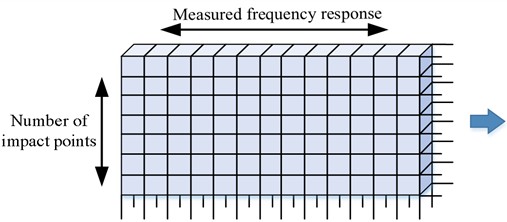
a) Input of samples

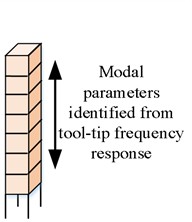
b) Output of samples

5. A demonstrative study

In this study, the FRFs of the KUKA KR90 robot, identified through modal testing experiments in reference [16], are used as raw experimental data to predict the multi-mode FRF. The testing setup involves an instrumented hammer with a force sensor and three accelerometers to excite and measure force and acceleration signals. The roving hammer technique was employed to impulse 23 points distributed across the robot's three links, as shown in Fig. 6, including three directions at point 21. To investigate the posture-dependent dynamics of the robot, modal testing experiments were conducted under three different postures: rigid posture, upright posture, and milling posture. As a result, a total of (21×3×3) FRFs were obtained, with a frequency resolution of 0.5 Hz and a bandwidth of 200 Hz. Consequently, (21×3×3×401) original FRF features can be obtained.

Fig. 6Three robot postures studied using modal testing experiments [17]: a) posture 1: rigid configuration: q1= 0°, q2= 135°, q3= 140°; b) posture 2: upright configuration: q1= 0°, q2= 135°, q3= –100°; c) posture 3: milling configuration: q1= 0°, q2= 70°, q3= 100°

a)

b)

c)

Modal parameters of point 21 in the three postures are identified using LSCE implemented in the LMS Test Lab Rev. 16A, as shown in Appendix Table A1. This includes a direct FRF ($FR{F}_{zz}$) and two cross FRFs ($FR{F}_{xz}$ and $FR{F}_{yz}$). The corresponding modal parameters, including natural frequencies $f_n$ and damping ratios ${\zeta }_n$, are arranged in Table 1. Furthermore, following the sample representation method shown in Fig. 5, 9 input tensors of size$$(20×401) and the corresponding 9 output vectors of size (10×1) are constructed, where the different postures and FRF types are considered.

For verification, 6 sets of input tensors and output vectors in two postures are selected as training samples, while the input tensors and output vectors of the direct FRF in the other postures are chosen as test samples to predict the modal parameters. Specifically, the modal parameters for the rigid posture, upright posture, and milling posture are predicted using the developed method. The prediction results are obtained by implementing the developed method in MATLAB and running it 20 times. These results are shown in Table 2, where the values in parentheses represent the experimental values extracted from Table 1. Additionally, a total of 10 visual samples are generated using the CKELMAI-enabled complex virtual sample generation method. During the generation process, the weights for the ten outputs (first-to-fifth-order natural frequency and damping ratio) in Eq. (15) are set as follows: 0.7, 0.04, 0.04, 0.01, 0.01, 0.1, 0.04, 0.04, 0.01, and 0.01. These weights are used to obtain an appropriate set of kernel parameters and cost parameters by the method described in reference [32].

The table demonstrates that the developed method for predicting modal parameters yields highly accurate results across various postures (Rigid, Upright, and Milling). The predicted values closely match the real values, with minimal discrepancies observed in most cases. The standard differences (Std) are small, reflecting the precision of the predictions. For example, Mode 1 shows strong alignment with the real values in the “Rigid” posture, with minor deviations in the other postures. Similarly, Modes 2 to 5 also show accurate predictions, with small variations primarily in the “Upright” and “Milling” postures. Overall, the method proves reliable for modal parameter prediction, as it consistently provides predictions close to the real values, with only slight variations and low standard differences, indicating the effectiveness and robustness of the method.

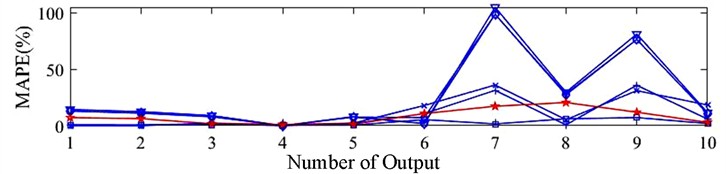
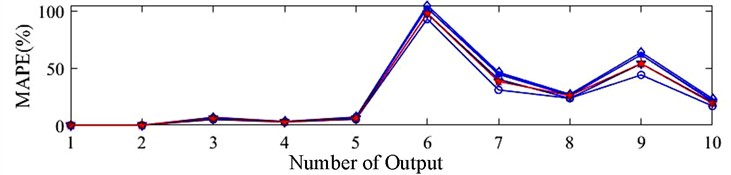
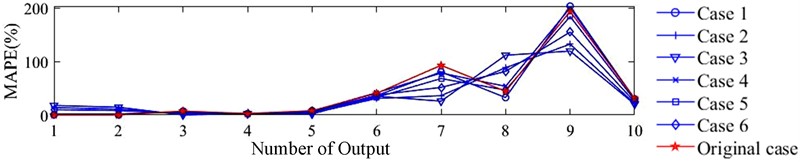
To further verify the low requirement of this method for the number of modal testing experiments, 5 out of the 20 hammer points on the robot body are selected to construct the feature tensors. Additionally, to examine the impact of hammer position on the prediction results, the combinations of the 5 hammer points are defined as {1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20}, {1, 5, 9, 13, 17} and {4, 8, 12, 16, 20}. For the sake of simplicity, these 6 cases are numbered as 1 through 6, respectively. The predicted results are shown in Table 3, with a corresponding prediction error (MAPE) diagram presented in Fig. 7. This allows for a more intuitive analysis of the prediction results, where “Original case” refers to the prediction results shown in Table 2.

The table clearly demonstrates that using five groups of impact experiments can effectively predict the modal parameters of the tool tip. In fact, for certain modal parameters, the prediction accuracy achieved with partial combinations of hammer points surpasses that obtained from the 20 groups of hammer experiments. Notably, in all tables throughout this paper, frequencies highlighted in dark gray represent the most accurate predictions, while those in light gray correspond to the second most accurate predictions. This suggests that the method is not only efficient but also capable of achieving higher prediction accuracy with fewer experimental setups. It underscores the effectiveness of selecting optimal hammer points for modal testing, as the approach consistently delivers precise results even with reduced experimental complexity.

Fig. 7Prediction error of modal parameters under different hammer locations combination: a) rigid configuration; b) upright configuration; c) milling configuration

a)

b)

c)

From Fig. 7, it can be concluded that no single combination of hammer points shows an absolute advantage under the Upright and Milling postures. However, the five groups of impact experiments are fully capable of performing the prediction tasks that is previously completed using 20 groups of impact experiments. In fact, even under the Rigid posture, Case 5 outperforms the 20 impact experiments in terms of prediction accuracy for all 10 modal parameters. Additionally, the setting of weight coefficients for the output modal parameters plays a crucial role in the prediction results. When the kernel and cost parameters are configured, the multi-output limit learning machine must balance trade-offs among the ten output modal parameters. This explains why, as seen in Fig. 7, the prediction accuracy is closely related to the weight parameters set; modal parameters with smaller weights tend to show less satisfactory prediction results. To obtain higher prediction accuracy, kernel parameters and cost parameters is set for ten output modal parameters respectively, and ten modal parameters are predicted in turn. The prediction results are as follows:

Fig. 8Prediction error of modal parameters under different hammer locations: a) rigid configuration; b) upright configuration; c) posture 3: configuration

a)

d)

b)

c)

The predicted values in Table 4 closely match the real values, with small discrepancies observed across all modes and postures, indicating high prediction accuracy. Std are minimal, further confirming the reliability of the method. For example, Mode 1 shows excellent alignment between the predicted and real values across all postures, with small deviations in the “Milling” posture. Mode 2 also shows strong prediction accuracy for the “Rigid” and “Upright” postures, while the “Milling” posture shows a slight increase in the standard difference. Modes 3 to 5 follow a similar pattern, with predictions being highly accurate and minor variations in standard differences. Overall, the results indicate that the method is highly effective for predicting modal parameters, with predictions consistently aligning closely with the real values. The small standard differences across all modes suggest that the method performs well under different postures and can provide precise and reliable modal parameter predictions with minimal error.

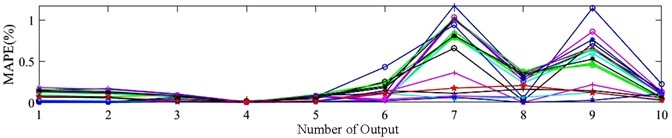
To further verify whether the developed method can achieve accurate prediction of the multi-mode FRF using only a set of impact experiments on the robot's body, the FRF corresponding to the 20 impact points on the robot body is used as the original data in turn for the prediction of the FRF, as shown in Appendix Table A2. In this case, the weights for the ten outputs in Eq. (15) are also set as 0.7, 0.04, 0.04, 0.01, 0.1, 0.04, 0.04, 0.01, 0.01, and 0.01, respectively, which are the same as those in Table 2 and Table 3. Moreover, a corresponding MAPE diagram is presented in Fig. 8 to provide a more intuitive analysis of the prediction results, where “Original case” refers to the prediction results shown in Table 2.

It can be concluded from Fig. 8 that it is difficult to identify a single hammer point that shows an absolute advantage under the Milling posture, the prediction accuracy achieved with the FRF from hammer point 11 under the Upright posture is significantly better than the results obtained from the 20 impact experiments. Similarly, under the Rigid posture, the prediction accuracy using the FRF from hammer points 4, 5, 15, 16, 17, and 19 outperforms the results of the 20 impact experiments. This confirms that the method can provide reliable and accurate multi-mode FRF predictions with only one set of impact experiments, and certain hammer points can yield superior results depending on the posture.

The above result indicates that if the impact position is appropriately selected, the developed prediction method can be used to predict the multi-mode FRF with only one impact test experiment, effectively predicting the multi-mode parameters of the tooltip. However, the selection of the hammer point needs to be analyzed and verified through pre-experimentation. To achieve higher prediction accuracy, taking hammer point 17 as an example. Kernel parameters and cost parameters are set for the 10 output modal parameters, and these 10 modal parameters are predicted in turn. The predicted results are as follows:

The results in Table 5 demonstrate that by selecting an appropriate impact position (e.g., hammer point 17), the developed prediction method can effectively predict the multi-mode FRF parameters with only one impact test. The predicted modal parameters closely align with the real values, with minimal discrepancies and low Std. Across all modes and postures (Rigid, Upright, and Milling), the predictions are accurate, with only slight variations in the standard differences, suggesting the method’s reliability. The results confirm that careful selection of the hammer point and the proper application of the prediction method can yield precise modal parameter predictions, which are essential for accurate modal analysis.

In addition, we assessed the time efficiency of our method for both training and prediction across various experimental setups. As reported in Table 6, training times remain uniformly low – between 6.25 and 6.58 seconds – regardless of the number of hammering points or the robot’s posture, underscoring the method’s consistent training efficiency. Even more impressive is the prediction latency: it stays at approximately 2.7×10⁻³ seconds in every configuration. Such a minimal prediction time ensures true real‑time operation, making the approach ideal for applications demanding rapid response. Altogether, these findings demonstrate that our method combines low computational overhead with the ability to deliver fast, real‑time predictions under diverse experimental conditions.

6. Conclusions

The accurate prediction of multi‐mode FRFs in milling robots is essential for maintaining process stability, efficiency, and workpiece quality. Traditional FRF prediction approaches often demand extensive experimentation, intricate modeling, and lengthy computations. To overcome these challenges, this study has introduced a novel feature‐transfer–based method that significantly reduces experimental effort while preserving prediction accuracy. Instead of relying on detailed joint‐space stiffness and inertia identification, the proposed approach requires only a small number of impact tests. Measured FRFs at selected points on the robot body – under both source and target postures – are organized into second‐order complex tensors, enabling effective feature transfer between configurations. Multi‐mode parameters at the tool tip are extracted via the LSCE method and assembled into label vectors for the source domain. A CKELM‐AI is then trained to predict the tool‐tip FRF under new postures. To enrich the training set, a CKELM-AI-based virtual sample generation strategy generates complex samples from the source‐domain tensor and label vectors. Additionally, feature augmentation – including frequency, statistical, and time–frequency feature extraction – further enhances model performance.

Validation results show that, even with only a few – or in some cases a single set of – impact tests, the proposed method delivers robust, high‐accuracy FRF predictions across various robot postures. Its low experimental burden and strong practical applicability make it an attractive solution for industrial‐scale robotic milling. Future work will focus on systematically investigating the influence of impact‐point selection on prediction accuracy, enabling guidelines for optimal sensor placement and further generalizing the method to different robot architectures.