Performance assessment and optimization of multi-rotor versus single-rotor turbine in Norwegian offshore wind farm’s

1.1. Background

In 2020, the European commission presented its strategy for expanding Europe’s renewable offshore energy capacity [1]. As part of the Commission's initiative to make Europe climate neutral by 2050, 300 GW of installed offshore capacity must be realized. In 2020, Europe had a capacity of 12 GW, meaning its current capacity needs to be increased by almost 30 times [1]. In order for Europe to reach this goal, Norway has to dramatically increase its investments in offshore wind energy. In contrast to Norway's thorough experience with offshore oil production, the country is relatively new to offshore wind farms (WF). Currently, the only operational offshore WF in Norway is Hywind Tampen, containing 11 wind turbines (WT) [2]. In 2020, the Norwegian government announced the opening of several sites along the coast for the development of renewable offshore energy [3]. This paper will focus on two of these sites, namely Utsira Nord and Sørlige Nordsjø II.

One of the main issues when designing WFs are the challenges posed by wake effects. Research indicates that wakes induced by WFs could reduce the overall energy production for down-stream WFs by as much as 20 % [4]. This would lead to a substantial reduction in revenue, while possibly disincentivizing further renewable offshore developments. The development of different types of turbine systems poses opportunities for the future of WFs. The concept of MR turbine systems, characterized by floating, vertical arrays hosting numerous smaller turbines, lacks a comprehensive comparison to traditional SR turbines. Despite their potential, the lack of comparison between systems hinders an understanding of their potential advantages.

1.2. Wind turbine types

The two main turbine configurations considered in offshore wind development are single-rotor (SR) and multi-rotor (MR) systems. Each presents unique advantages and challenges, particularly in the context of wake effects and maintenance. This section outlines their core characteristics.

Single-Rotor (SR) Turbines – Horizontal Axis wind turbine Almost all commercial WTs today are built on the horizontal-axis design principle. Like airplane propellers, these turbines usually have either two or three blades, with their axis of rotation parallel to the ground. Its design allows for precise control of the turbine speed via changing the blade pitch [5]. These WTs come in a myriad of sizes with ranging power production capabilities. The blade size of the turbine is the determining factor for the power production [6]. Small-scale turbines often installed on single homes have capacities ranging between 400 Watts and 100 Kilowatts. These typically range in diameter between 1 and 15 meters. On the other end of the spectrum, the largest commercial-scale turbines can currently reach diameters of 240 meters with capacities up to 15 Megawatts [6], [7]. Assuming optimal wind conditions, one of these turbines could generate enough power annually to supply over 4 500 Norwegian households [8]. Fig. 1 shows a typical configuration as well as the main components of HAWTs.

Fig. 1Diagram of the main parts and components of HAWTs [9]

Multi-Rotor (MR) Turbine Systems MR turbine systems is an innovative alternative to the classic SR turbines. Instead of each turbine operating as a stand-alone unit, MR systems contain many smaller rotors in a cohesive framework [10]. SRs have large rotor blades which makes it possible to capture large amounts of energy. The alternative solution posed by MRs is the collective power generation of multiple smaller rotors in a system, making up for their reduced individual power output. Companies specializing in MR technology are working on improving their designs and making them a realistic option to SRs. The improvements aim to extenuate up-time and simplify maintenance, thereby making them a cost-effective alternative to SRs [11]. This would strengthen the prospect of the MR as a promising alternative within the renewable energy sector.

The Windcatcher provides remarkable efficiency, where five units would be capable of generating the same amount of electricity as 25 SRs. This efficiency stems from the strategic grid-like positioning of the turbines [12]. A notable advantage in the Windcatcher design is its maintenance efficiency. With SRs, maintenance typically results in a complete halt in energy production, potentially causing the turbine to remain offline for months [11]. In contrast, the setup for the Windcatcher allows for targeted maintenance where only the affected rotor would need to be offline [11].

Fig. 2Digital rendering of the “Windcatcher” at sea [16]

The remaining turbines would continue their operation, leading to more consistency in energy production and minimizing revenue losses related to downtime [12].

The Windcatcher also offers another advantage: it eliminates the need for a specialized watercraft. This is because the Windcatcher has its own self-contained maintenance infrastructure [13]. In contrast, the longer downtime of SRs is mainly caused by their larger rotor sizes, making them require specialized transportation and caution [11]. The smaller rotors of wind-catching systems not only facilitate transportation, but also contribute to decreased downtime, thereby enhancing their overall logistical efficiency [12].

Vertical-Axis Wind Turbines: Vertical-axis WTs (VAWTs) are WTs that rotate their airfoil blades about a vertical axis. These turbines predate the conventional and horizontal propeller-style turbine by over 1000 years, with evidence of construction being found in ruins dating back to 200 BCE in Persia [14]. The two most common types of VAWTs use either the Darrieus or the Savonius airfoils (see Fig. 3), which are drag-driven and lift-driven, respectively [14]. Due to the limited output of drag-driven turbines, lift-driven designs have seen the most commercial use [14].

Fig. 3Illustration showing the most common VAWT types [14]

VAWTs have not seen the same technological advancements as their horizontal counterparts. The main problem with VAWTs is that they have been unsuccessful at matching the overall efficiency and power output of traditional HAWTs. Their strongest feature is that they do not need to be oriented in the wind direction to work optimally. In addition, due to the fact that the axis of rotation is much closer to the center of gravity they are generally more stable [14]. Due to their comparatively smaller footprint and different wake effects, VAWTs can be placed much closer together, allowing for a greater overall power density [15].

1.3. Objectives

The aim of this paper is to compare the optimized layouts of SR and MR systems based on AEP at Sørlige Nordsjø II and Utsira Nord. To achieve this main objective we have accomplished the following sub-objectives:

1) Construct the MR object in python.

2) Optimize the WF layouts.

3) Conduct a comparison of the AEPs for MR and SR configurations.

2.1. Constructing the wind site object

In order for the optimization task to be accurate and valid, the wind conditions at each of our sites was modeled using meteorological data from NASA’s Earth Science Division Applied Sciences Program [16]. Upon running performwindanalysis.py [17], the script records the input for selecting which geographical area to analyze and uses the integrated Data Access Viewer Enhanced tool (DAVe) to retrieve daily wind data, spanning the past five years. The Wind Speed and Wind Direction at 50 meters above sea level are selected as parameters before retrieving the data as a CSV file. The file is then formatted and sorted for further processing.

Once the CSV data has been correctly formatted, a wind rose is then constructed and plotted. Subsequently, the average wind speeds are calculated and graphed according to a Weibull Distribution. Python’s built-in Weibull function is utilized to fit the data based on relative probabilities. Afterwards, both the wind speeds and their corresponding relative probabilities are presented in the form of Weibull shape and scale factors. The wind speeds are further categorized according to the wind sector they originate from. A total number of twelve sectors was chosen, making each sector 30 degrees wide. Then, applying the Weibull fit function to data from each sector yields Weibull factors for each corresponding wind sector. The number of wind instances in each sector is divided by the total number of instances to produce sector frequencies.

2.2. Optimization

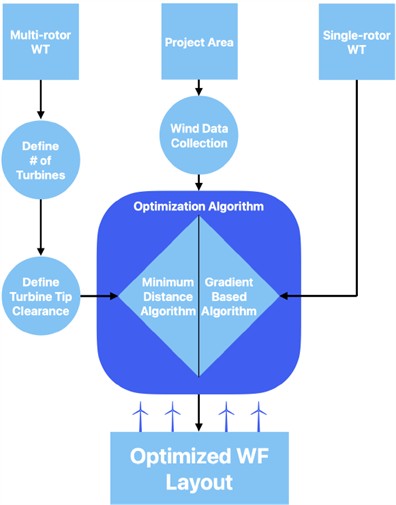
For simulating wake effects, we have used PyWake. Wake modeling has been done using the Jensen/Park model [18]. TopFarm was used for optimizing the SR WF layouts [19]. The functionalities of both PyWake and TopFarm will be explained more thoroughly in Section 2.3 and 2.4.

The objective function we are trying to maximize given the spatial constraints of our sites is the AEP function. This function is defined as follows [20]:

The variable $p_j$ represents the probability of occurrence of each wind instance. $P_j$ represents the sum of the power output from all WTs for a specific wind instance. Wind data is converted into 540 $j$ instances. The scalar in front converts the power output to GWh/year, which is a common measurement of power production.

2.3. Understanding PyWake

Site Object and Wind Turbine Object. An important component of PyWake is the site object. The site object defines the wind speeds and their respective probabilities from each direction, like a wind rose. There are three different site classes available to define our site. These are UniformWeibullSite, WaspGridSite and XRSite [18]. Four parameters used to define the site object are the Weibull scale parameter, the Weibull shape parameter, the sector frequency, and the turbulence intensity [18]. The main parameters of the WT object are the thrust coefficient, the power curve, the turbine diameter and the hub height [18].

Modeling Wind Farms The coordinates of the WTs are the only parameters necessary for modelling a WF layout. The layout is modeled by defining a list of $x$-coordinates, $y$-coordinates, and optionally another one for $z$-coordinates. If the $z$-coordinate list is not defined, the height of the turbines will be set to a predefined hub height. All the turbines in a WF are assigned to an index of these lists.

Wind Farm Simulation After defining the site object, WT object, and the $x$ and $y$ coordinates for the turbines, the WF’s AEP can be simulated. Different sets of turbine coordinates give different values of AEP as a consequence of the wake effect.

2.4. Single-rotor WF optimization

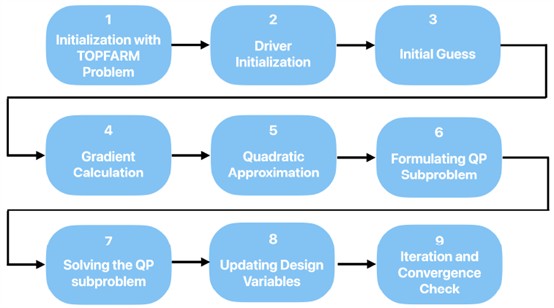
Optimization With TopFarm TopFarm is a Python module Developed by DTU Wind Energy. One of its functionalities is optimization of WF layouts. The TopFarm package can utilize different wake models for flow simulations [19]. OpenMDAO is an open-source platform with Python-based optimization tools for engineering problems. Within OpenMDAO’s library are optimization drivers. The driver serves as a computational tool for finding the most optimal solutions for a given problem [19]. In essence, it is an object that includes instructions for various optimization procedures. The driver most commonly used in TopFarm is called EasyScipyOptimizeDriver [19]. The default algorithm utilized by this driver is Sequential Least Squares Quadratic Programming (SLSQP), which is a gradient-based optimization procedure [19].

Gradient-based Optimization Gradient-based optimization can be explained using the landscape analogy as done in [21]. To optimize the layout of a WF, it is essential to define the design variables and the objective function accurately. The design variable vector $x$ has 2$N$ variables, where $N$ represents the number of turbines in a WF. $x_i$ and $y_i$ represents the $x$ and $y$ coordinate of the $N$th turbine in the WF:

The objective function $f\left(x\right)$ represents a 2$N$ dimensional landscape of the AEP, and is a function of the design variable vector $x$. The objective function is defined by the PyWake module PyWakeAEPCostComponentModel. The AEP is calculated by Eq. (1):

Subsequently, the gradient of $f$ is calculated in Eq. (4) and utilized to minimize the objective function $f\left(x\right)$. The gradient represents the direction of steepest decent in the 2$N$ dimensional landscape. Fig. 5 demonstrates the steps involved in the gradient based optimization process:

2.5. Multi-rotor WF optimization

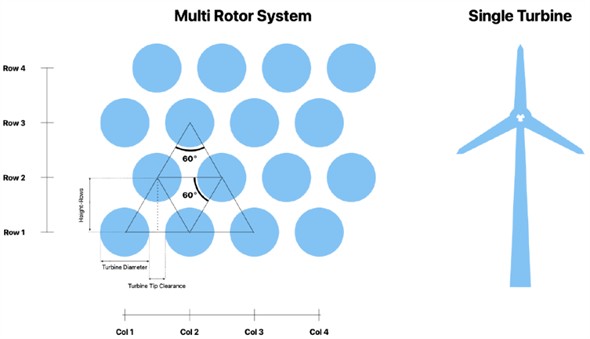
Considering there is currently no template for modelling MRs in PyWake, a variety of relations must be defined. MRs are in simple terms organized groups of many SRs. The SRs are defined in PyWake by their $x$, $y$ and $z$ coordinates. Therefore, relations between $x$, $y$ and $z$ coordinates are defined to group SRs into MRs. By writing a function we can automatically output the $x$, $y$ and $z$ coordinates of all the turbines in MRs. The inputs are the systems center coordinate, its number of rows and columns, the turbine diameter, and the turbine tip clearance. In accordance with the design by Wind Catching Systems AS, we model the turbines to be in a triangular grid with a 60 degree offset between turbine rows, as shown in Fig. 5.

Fig. 5Step-by-step summary of gradient-based optimization process

Minimum Distance Multi-Rotor The minimum distance between MR systems is defined in minimumDistance.py [17]. The wind conditions and the number of rows and columns are taken as inputs, and the minimum distance is returned. First the wind sector with the largest mean wind speed is detected and set as a reference for the following AEP calculations. Before the algorithm runs, the total AEP of two MR systems 20 km apart is calculated. This serves as the reference AEP when the effects of wakes are negligible. Subsequently, we loop through the following calculations.

Fig. 6Simple illustration of the MR system showing configuration and scale

Initially, we calculate the AEP for two MR systems positioned 100 meters apart. The distance is then increased in 100-meter increments, calculating the AEP after each step. We continue this process until one of the following conditions are met: The AEP reaches 99 % of the reference AEP, or the last iteration fails to yield an additional GWh of AEP. When either of these conditions are met, the current distance is returned as the minimum. The reasoning behind the last condition is that we assume that a hundred meters of added distance requires an additional hundred meters of power cable. Installation of a 100 meters of sub-sea power cables cost around 100 000 pounds [22]. Also, we assume an electricity price of approximately 100 000 pounds per GWh [23]. Mathematically, increasing the minimum distance of 100 meters will still be profitable if it results in at least one additional GWh of AEP.

In multiRotorPosition.py the coordinates for the MRs are defined [17]. The inputs are the number of MRs, the outer boundary of the map and the minimum distance between each system. Every MR system will be added to the map incrementally. Each new coordinate has to meet specific conditions to be allowed. First, the distances between the new candidate MR and all previously added MRs must exceed the minimum distance defined previously. Furthermore, an inspection ensures that the candidate MR lies within the boundaries of the map. If the candidate fails to meet either of these conditions, it is discarded, and a new coordinate point is generated.

3.1. Defining wind turbine objects

Single-Rotor Turbine When modeling the SRWT, the IEA Wind 15-Megawatt Offshore Reference WT is used as a reference [7]. The turbine has a power rating of 15MW, cut-in speed at 3 m/s, rated wind speed at 10.59 m/s, and cut-out speed of 25 m/s. The diameter of the turbine is 240 meters, and the hub height is 150 meters [7].

Multi-Rotor Turbine Specific power and thrust coefficients for the individual WTs in our MR system are inspired by the Mitsubishi MWT-1000 turbine. It has a power rating of 1 MW, cut in speed at 4 m/s, rated wind speed at 13.5 m/s, and cut out wind speed at 25 m/s and has a diameter of 57 meters [24]. In reality, MR WTs could have varying diameters depending on its design. We currently assume the power and thrust properties for all prompted diameters to be equivalent to the MWT-1000’s properties.

3.2. Results from Sørlige Nordsjø II

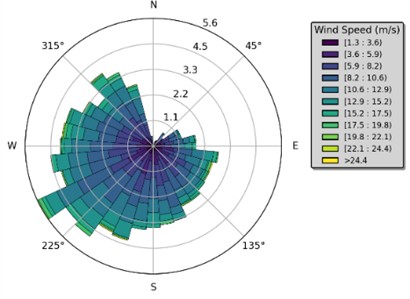
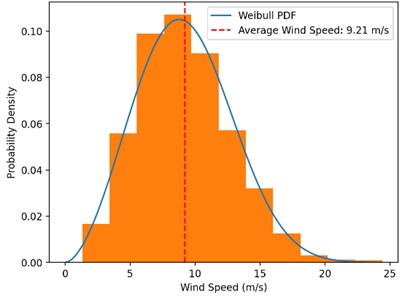
The wind rose in Fig. 7, shows that the wind most commonly originates from the southwestern quadrant. The wind has the lowest probability of originating from the northeast direction. The probability distribution graph shows that the mean wind speed is 9.21 m/s, with a relative probability of occurrence of about 10 %. The shape of the distribution curve shows higher probabilities for speeds close to the mean and decreasing probabilities for higher or lower speeds.

3.2.1. Single-rotor turbines at Sørlige Nordsjø II

In accordance with SNII's established capacity of 1500 MW, we used 100 SRs rated at 15 MW each. After 428 iterations, we obtained a maximum total AEP of 8077.93 GWh. Fig. 8 shows the far (left) and detailed (right) view optimized positions of the turbines, and Fig. 9 shows the AEP development. The detail view shows a marked clustering towards the eastern side of the map, and some minor voids located at the west end, center, north, and south of the project area.

Fig. 9 shows that for a total of 428 iterations the AEP increased by 1.22 %. Specifically, the resulting layout yields 1.22 % better AEP than random positions. We observed a rapid increase throughout the first hundred iterations with a growth from around 7980 GWh to about 8045 GWh. From iteration 100 to around 260, the growth became slower, but still increased to approximately 8070 GWh. The remaining 150 iterations experienced a stagnation in growth, producing an additional 7 GWh.

Fig. 7Illustrations showing the wind conditions at Sørlige Nordsjø II

3.2.2. Multi-Rotor Systems at Sørlige Nordsjø II

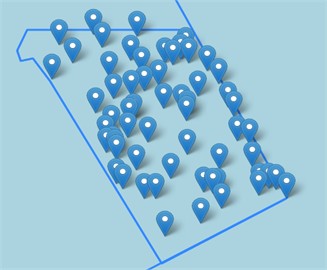
Utilizing the selected parameters for MRs, 60 systems containing a total of 1500 WTs rated at 1 MW each met the capacity requirements for the area. This configuration yielded a maximum AEP of 7002.23 GWh. The resulting AEP for MRs is 13,2 % lower than the SR counterpart. Fig. 10 shows the final locations of each MR system. In contrast to the SR results, where there is clustering in the east portion of the map, multiple MRs are aligned from the southwest to the north. Large open spaces are present in the northwest and southeast. The cluster line is parallel with the frequent winds coming from southwest, based on the wind rose in Fig. 7.

Fig. 8Map displaying the optimized SR locations for SNII

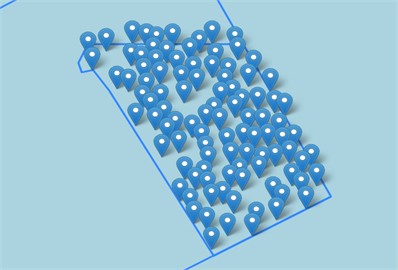
Fig. 9Graph illustrating the improvement in AEP over the course of optimization iterations

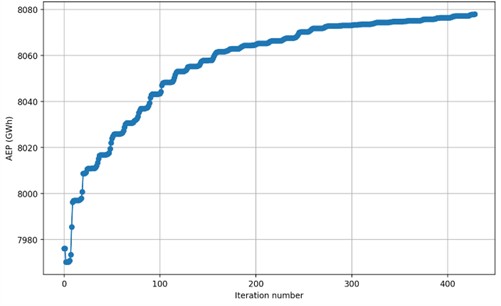
Fig. 10Map displaying the optimized MRS locations for SNII

3.3. Results from Utsira Nord

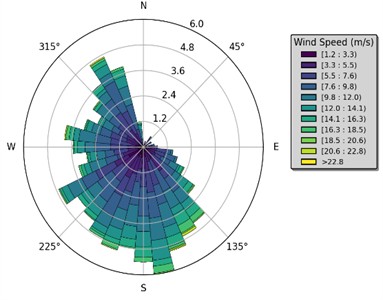
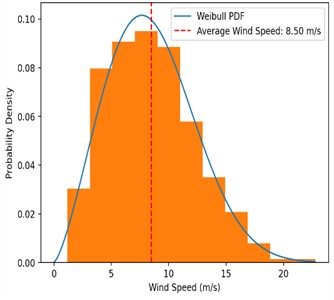
As seen in the wind rose, the wind has the highest probability of originating from the southern region. The wind has the lowest probability of originating from the north and east directions. The probability distribution graph shows the wind speed being centered around 8.50 m/s, occurring about 9.5 % of instances. As previously observed in the probability distribution graph for SNII, wind speeds surrounding the average speed experienced a similar spread, slightly tending towards the lower end of the spectrum.

Fig. 11Illustrations of the wind conditions at Utsira Nord

Single-Rotor Turbines at Utsira Nord Our simulation produced a total AEP of 2436.94 GWh. Since the project area’s capacity is 500 MW, we employed 33 turbines rated at 15 MW. Fig. 12 shows the optimized position of each WT, while Fig. 9 shows the AEP development.

Fig. 12Map of optimized SR layout at Utsira Nord

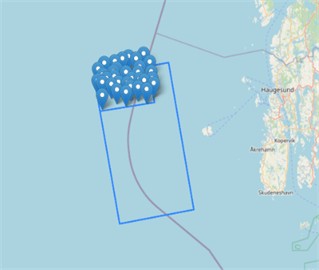
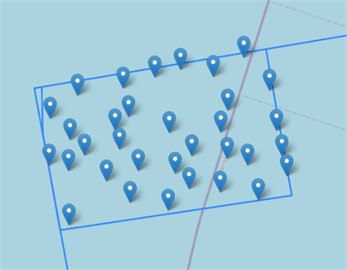
Fig. 12 shows both a far view and a detailed view of the turbine locations. There is an open space on the southwest side of the map. Another open space is present in the central northern edge. Several turbines also appear to be clustered around a diagonal, stretching from the southeast to the northwest.

Fig. 13Graph illustrating the improvement in AEP at Utsira Nord over the course of optimization iterations

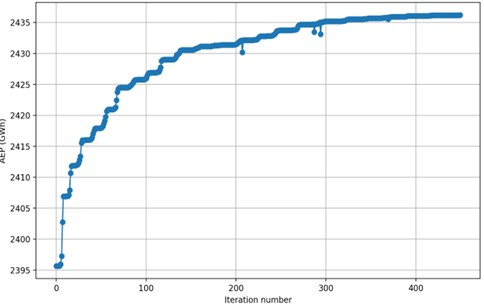
The AEP for Utsira Nord experienced a growth of 1.75 % throughout 450 optimization iterations. Specifically, the resulting layout yields 1.75 % better AEP than random positions. The graph shows an initial rapid growth before seemingly plateauing after about 300 iterations. During the first 100 iterations the AEP grew from 2395 GWh to approximately 2426 GWh. Between iterations 100 and 300 the growth became slower but continued to rise to 2435 GWh. The remaining 100 iterations experienced significant stagnation and produced one additional gigawatt-hour of AEP.

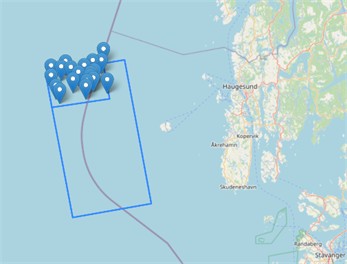
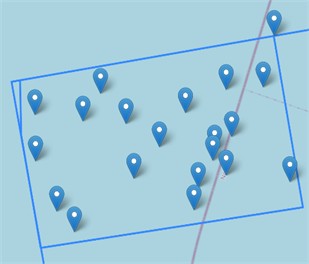
Multi-Rotor System at Utsira Nord The selected parameters for MRs resulted in 20 systems at UN. This includes 500 WTs rated at 1 MW each. The simulation yielded an AEP of 2175.13 GWh. The resulting AEP for MRs is 10.8 % lower than the SR configuration. Fig. 14 show the location of each MR system.

In left part of Fig. 14 we see a far view of the MR system locations at UN. While right part shows a detailed view where a large open space is present in the south-west. Additionally, multiple MR systems cluster in a line from the southeast, stretching north.

Fig. 14Map displaying the optimized MR locations for UN

3.4. Result discussion

Despite SNII’s expected AEP of 7000 GWh, our SR-simulations yielded a total of 8077.93 GWh, while the MR systems yielded 7002.23 GWh. Furthermore, the expected AEP for UN was 2000 GWh. Like before, our simulated AEP using either turbine configuration surpassed this, producing a maximum AEP of 2436.94 GWh and 2175.13 GWh for the SR and MR systems, respectively.

When optimizing the turbine positions, similar outcomes were observed for both project areas. SR turbines consistently outperformed the MR systems, yielding at least 11 % more AEP every time. A notable observation is that the maps of the turbine layouts all contain distinct clusters and voids. The SR position layout for SNII includes a cluster that follows the eastern border of the area. The reason for this occurrence is likely related to the wind conditions. As we discovered, the wind at SNII usually originates from the south/southwest area. The resulting configuration likely originates as a result of minimizing the overall wake interactions.

Regarding the MR layout at SNII, a cluster of systems stretch from the south-west to the north-east part of the area. This cluster would result in unfavorable wake effects on a large portion of the systems. In addition, there is a void in the south-west corner of the project area. There seems to be an imbalance in the placement of systems, meaning our optimization strategy did not work.

The SR layout at UN seems evenly scattered, although this area contains far less WTs than SNII. In contrast to SNII, the MR layout also seems to be evenly distributed, except for a slight cluster to the east of the center. This could potentially explain why the AEP for the MR layout at UN more closely aligned with the results for the SR layout. We believe the minimum distance strategy may have been insufficiently defined. This might be the reason for the unfavorable positioning of the MRs at SNII. As for the resulting AEP deficit, the income loss could be compensated for with the MR system’s highly efficient maintenance procedures and minimized downtime, as described in Section 1.2.