Abstract
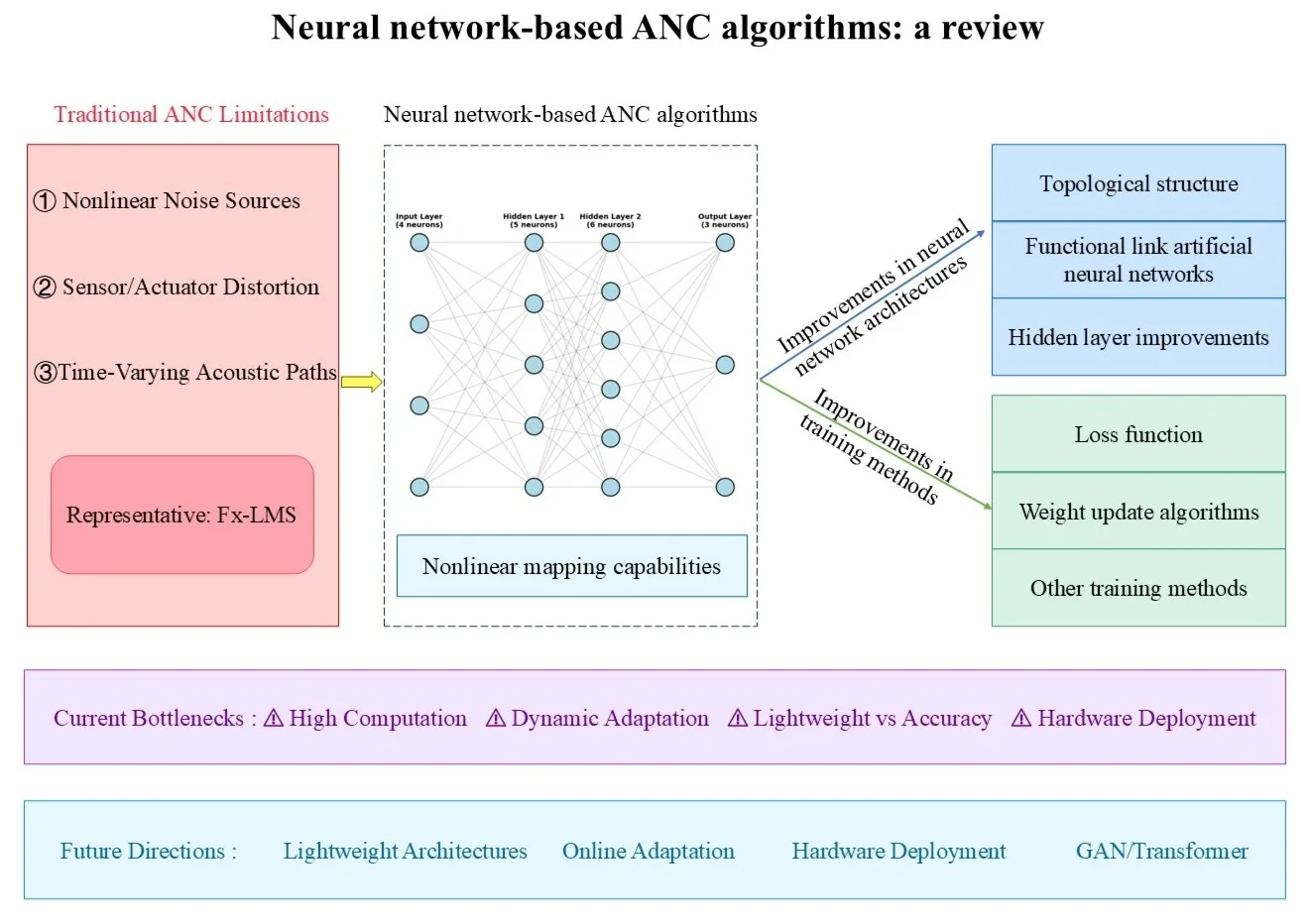
Active Noise Control (ANC) technology is of great value in the field of noise mitigation. Recently, traditional linear adaptive control methods, represented by the FxLMS algorithm, are structurally simple and computationally efficient but often suffer from performance degradation or even failure in practical applications due to nonlinear system factors. For this reason, neural network-based ANC methods have attracted significant research interest for their strong nonlinear processing capabilities and have gradually emerged as a focal point for addressing nonlinear ANC problems. This paper systematically reviews the research progress of neural networks in the field of nonlinear ANC, focusing on two key dimensions: network architecture and training methods. In terms of architecture design, existing studies primarily enhance performance through topology optimization, improvements to functional link artificial neural networks, and innovative hidden layer designs. Advancements in training methods focus on the optimization of loss functions, innovation in weight update algorithms, and the introduction of other training strategies. In the future, neural network-based ANC algorithms will continue to deepen, with potential development paths including the integration of advanced network architectures such as Generative Adversarial Networks (GANs), optimization of utility functions, pruning of hidden layers, improvement in loss function design, and the adoption of more efficient training strategies. These efforts will further improve algorithm performance and ultimately provide robust support for achieving more precise and efficient active noise control.
Highlights
- Review and comparison of neural network-based ANC algorithms focusing on network architecture and training methods.
- Analysis of advantages and disadvantages of current neural network-based ANC algorithms.
- Identification of current bottlenecks limiting neural network-based ANC development and future research directions.
1. Introduction
Mechanical equipment in industrial plants and construction sites generate noise during operation, which can be harmful to workers’ health. Passive Noise Control (PNC) techniques aim to reduce noise using sound-absorbing materials or barriers. While effective for high-frequency noise, they exhibit limited performance for low-frequency noise and may result in complex, bulky active noise systems. In this context, Active Noise Control (ANC) systems have emerged as a promising solution. The development of ANC can be referenced in the literature by George and Panda [1].
Traditional ANC algorithms are primarily based on adaptive filtering techniques (such as the Filtered-x Least Mean Square (FxLMS) algorithm and its variants). Under the assumption of linear time-invariant (LTI) systems, these algorithms optimize the weights of finite impulse response (FIR) filters to generate a secondary signal that cancels the noise based on the principle of destructive interference of sound waves. However, the presence of widespread nonlinear factors in practical engineering scenarios pose the following challenges to traditional ANC algorithms [2]: 1. Limited noise reduction capability when dealing with nonlinear noise sources; 2. Nonlinearities in system components (e.g., actuators and sensors) that cause distortion in the secondary signal; 3. Nonlinear acoustic paths that degrade noise reduction effect. Neural network-based ANC algorithms can effectively overcome the limitations of traditional linear ANC in nonlinear scenarios due to their core advantages – the powerful nonlinear mapping and universal approximation capabilities. Mathematically, neural networks construct hierarchical structures through nonlinear activation functions (such as ReLU and tanh). According to the universal approximation theorem, they can approximate complex functional relationships between noise sources and control signals with arbitrary precision, overcoming the limitations imposed by the linear framework of traditional Wiener filters.
Current research on neural network-based ANC algorithms primarily focuses on two directions: 1. Innovations in neural network architectures mainly reflect in the design of topological structures (such as the introduction of cross-layer connections and recurrent structures), functional linkage mechanisms (e.g., function-expansion type artificial neural networks), and the optimization of hidden layer components; 2. Improvements in training methods, involving the design of loss functions and the exploration of weight optimization strategies. Recently, most algorithmic advancements in this field have focused on optimizing these two directions. This paper provides a summary of related algorithms from both aspects.
2. Early developments of neural network-based ANC algorithms
Table 1 presents the early developments of neural network-based ANC algorithms, highlighting key innovations in their evolution. In the early stages, these algorithms mainly focused on Multilayer Perceptrons (MLPs) and Functional Link Neural Networks (FLNNs), which featured shallow architectures and were mainly used for nonlinear mapping.
Table 1Early developments of neural network-based ANC algorithm
Year | Authors | Innovations | References |
1997 | Tokhi and Wood | Applied Multilayer Perceptrons (MLPs) to ANC algorithms | [3] |
1997 | Tokhi and Wood | Proposed an active noise control algorithm based on Radial Basis Function (RBF) networks | [4] |
1999 | Tokhi and Veres | Introduced an intelligent adaptive active control scheme combining genetic algorithms and neural networks | [5] |
2000 | Zhang and Jia | Developed a neural network-based adaptive active nonlinear noise feedback control method | [6] |
2006 | Zhou and Zhang | Proposed a neural network controller based on Simultaneous Perturbation Stochastic Approximation (SPSA) for nonlinear ANC systems | [7] |
The earliest integration of neural networks with ANC algorithms was achieved by Tokhi and Wood. In 1997, they introduced a neural adaptive ANC system based on a multilayer perceptron (MLP) neural network. Additionally, they proposed a one-step-ahead (OSA) prediction mechanism for model training and a model predicted output (MPO) mechanism for model validation. These mechanisms enabled the MLP to drive the secondary source in real time by using the reference signal and historical output signals, allowing it to generate the secondary signal accordingly. This framework demonstrated modeling capabilities for dynamic systems. Experimental results showed that the system achieved approximately 20 dB noise reduction for broadband noise. However, a limitation of this approach was that when using the backpropagation algorithm to dynamically adjust the secondary signal, the network was prone to getting trapped in local optima [3]. In the same year, Tokhi and Wood proposed another ANC algorithm based on radial basis function (RBF) networks. This algorithm employed the same training and validation mechanisms as in literature [3], but differed from MLPs in that RBF networks achieve nonlinear mapping through radial basis functions – thin plate spline basis functions were used in this study. One of the main advantages of RBF networks is that their unknown parameters exhibit linear characteristics, which allows the network to find a global minimum on the error surface and ensures faster convergence. Simulations demonstrated that this algorithm achieved similar noise reduction effect as reported in literature [3]. Leveraging its learning and adaptive capabilities, the RBF-based algorithm could track changes in noise sources and system components, enabling online adjustment of controller parameters and overcoming the poor noise reduction performance of traditional linear ANC algorithms in dealing with system variations [4]. In 1999, Tokhi and Veres proposed an adaptive control framework that integrated multiple intelligent algorithms, marking the first time that self-tuning control, genetic algorithms, neural networks, and a supervised iterative adaptive mechanism were combined within a unified architecture. This approach addressed the challenge of broadband control in noise-vibration coupled environments. By replacing the gradient descent method with a genetic algorithm, the local optima was avoided. Experimental results in a free-field setting demonstrated an average noise reduction of 20 dB for broadband noise in the 200-500 Hz range and a 40 dB attenuation in vibration spectral peaks [5]. In 2000, Zhang and Jia proposed a neural network-based online adaptive active nonlinear noise feedback control method, specifically designed to handle nonlinearity in the primary path. Simulations showed that this method was capable of suppressing harmonics generated by nonlinearities – an effect that FIR filters could not achieve. However, the drawback was its significantly higher computational complexity compared to FIR-based methods [6]. In 2006, Zhou and Zhang proposed a neural network controller based on SPSA algorithm for nonlinear ANC systems. The controller used SPSA to calculate approximate gradients, thus eliminating the dependence on secondary path estimation and addressing the issue of time-varying secondary path modeling. In experiments, a noise reduction of 40 dB was achieved for a 300 Hz sinusoidal noise signal [7].
3. Improvements in neural network architectures
Innovations in neural network architectures can be categorized into the following three main directions: 1. Topology enhancements, which involve the introduction of new neuron connection patterns or layer types; 2. Improvements in Functional Link Neural Networks (FLNNs), focusing on expanding the noise signal at the input layer using functions; 3. Optimization of hidden layer algorithms, which aims to refine or introduce new algorithms based on specific requirements.
3.1. Topological structure
In the area of network structure improvement, Recurrent Neural Networks (RNNs) have emerged as the dominant architecture in neural network-based Active Noise Control (ANC) algorithms. Incorporating recurrent neurons into the network enhances the model’s memory capability, which offers distinct advantages for processing time-series data such as signals. Table 2 summarizes recent innovations in topological structures of such algorithms, including different network models and their respective advantages.
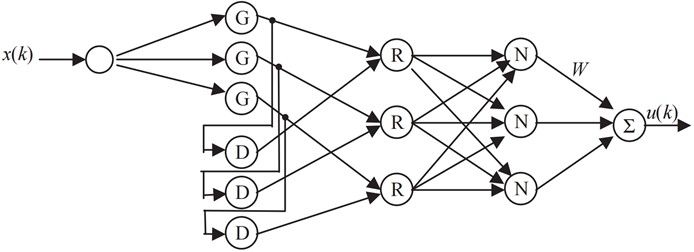
Zhang and Gan applied the Simplified Fuzzy Neural Network (SFNN) to ANC systems, reducing the number of parameters and achieving a computational complexity only one-eighth that of a traditional Fuzzy Neural Network (FNN). In experiments involving 100 Hz nonlinear harmonic noise, the SFNN outperformed the Multilayer Perceptron (MLP) in terms of noise reduction. This algorithm improves convergence speed while retaining nonlinear processing capability, making it well-suited for implementation on DSP platforms [8]. Fig. 1 shows the topology of the SFNN.
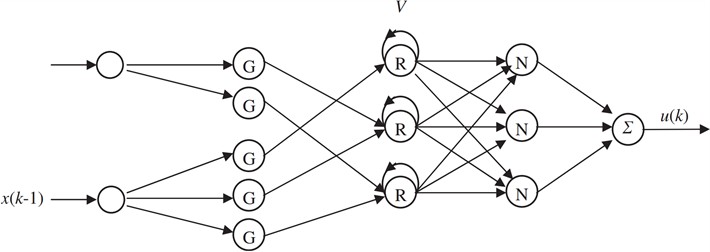
Building on this, they proposed an adaptive recurrent fuzzy neural network (RFNN) framework to address the issue of the static fuzzy neural network (SFNN) lacking dynamic memory capabilities and thus struggle to handle. The RFNN reduces the number of parameters by 40 % compared to the SFNN and increases the inference speed by 30 %. Simulation experiments demonstrate that in a noise scenario with a 100 Hz fundamental frequency plus 200 Hz harmonics, the RFNN achieves a 20 dB attenuation of the fundamental frequency and an 18 dB attenuation of the harmonics, yielding an 8 dB improvement over the SFNN [9]. Fig. 2 illustrates the topological structure of the RFNN, which introduces a recurrent structure based on the SFNN.
Table 2Summary of topological innovations
Innovations | Specific Operations | Advantages |
Simplified Fuzzy Neural Network (SFNN) | Simplifies the input structure and reduces the number of parameters | Faster convergence and lower computational complexity compared to Multilayer Perceptron (MLP) |
Adaptive Recurrent Fuzzy Neural Network (RFNN) | Introduces a recurrent structure | Possesses dynamic memory capability; suitable for handling time-varying noise |
Reinforced Even-Mirrored Fourier Nonlinear Filter (REMFNL) | Introduces a diagonal channel structure to represent cross terms and applies dimension reduction strategies to reduce computational complexity | Capable of modeling both linear and nonlinear recursion |
Adaptive Fuzzy Feedback Neural Network (AFFNNC) Controller | Combines fuzzy inference with an adaptive feedback neural network | Requires no pre-training |
Attention-based Recurrent Network (ARN) | Incorporates a delay-compensation training strategy and uses an improved overlap-add method for signal reconstruction | Enables deep ANC with smaller frame sizes, reducing algorithmic latency |
Notch Filter Based on Nearest Neighbor Regression (NNR) | Features a unique structure combining adaptive notch filtering and a residual control loop | Effectively enhances noise control and tracking performance |
Convolutional Recurrent Network (CRN) for Multichannel ANC | Uses CRN to perform complex spectral mapping for multichannel active noise control | Achieves multichannel output; suitable for noise control at multiple spatial locations and quiet zone generation |
DNN-based Nonlinear Active Noise Control Algorithm | Uses deep neural networks to model nonlinear relationships between input and output parameters | Stronger modeling capability and broader applicability |
Fig. 1Structure of the SFNN
Guo et al. proposed the Reinforced Even-Mirrored Fourier Nonlinear Filter (REMFNL) and its channel-reduced variant, which employs a diagonal channel structure to accelerate the computation of cross terms. This approach addresses the limitations of traditional recursive filters, such as low control accuracy for mixed noise due to the absence of linear recursive components and the lack of guaranteed stability in recursive structures. In scenarios involving chaotic, saturated, or real measured acoustic paths, the method achieved a 2-12 dB reduction in NMSE compared to baseline methods. Additionally, the stability control led to a 50 % improvement in convergence speed under disturbances [10]. Huynh and Chang proposed an Adaptive Fuzzy Feedback Neural Network Controller (AFFNNC), which integrates fuzzy inference and feedback neural networks through a five-layer architecture, enabling the system to respond to nonlinear disturbances in real time. The output layer directly adjusts filter parameters using an adaptive algorithm without the need for pre-training, significantly reducing computational complexity. Under comparable conditions, its multiplication operations account for only 1 % of those required by a Functional Link Artificial Neural Network (FLANN) [11]. Zhang and Wang introduced the Deep ANC framework, which reformulates active noise control as a supervised learning problem. This framework employs a Convolutional Recurrent Network (CRN) to directly learn the complex spectral mapping from the reference signal to the anti-noise signal. Through large-scale, multi-condition training, it achieves end-to-end optimization. In untrained noise and acoustic environments with nonlinear distortion, the proposed method outperforms FxLMS by more than 6 dB in noise attenuation (NMSE) [12]. Zhang et al. employed a notch filter based on Nearest Neighbor Regression (NNR) as an adaptive controller, featuring a unique structure composed of an adaptive notch filter and a residual control loop. This architecture significantly enhances noise control performance for narrowband tonal noise. By integrating NNR filter banks and an adaptive gain controller, it demonstrates fast convergence and strong tracking capabilities in both ideal and real noise control experiments [13]. Huang et al. proposed an end-to-end nonlinear active noise control algorithm based on Deep Neural Network (DNN). The innovation of this method lies in leveraging the universal nonlinear approximation capability of DNN to simultaneously model the coupling effects of the acoustic channel transfer function and speaker saturation nonlinearity. By directly optimizing the generation of anti-noise signals, the approach avoids the error accumulation problems associated with the step-by-step modeling of nonlinear components in traditional method [14].
Fig. 2Structure of the RFNN
3.2. Functional link artificial neural networks
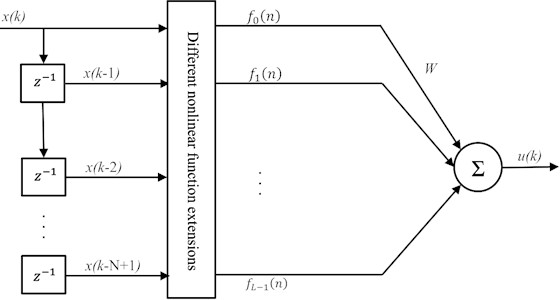
Improvements in Functional Link Artificial Neural Networks (FLANNs) have primarily focused on selecting various functional expansions of noise signals based on different application scenarios and designing tailored network architectures. These modifications aim to reduce computational complexity while enhancing the ability to process nonlinear noise. Fig. 3 illustrates the structure of a Functional Link Artificial Neural Network.
Table 3 summarizes various improvements related to functional-link artificial neural networks, primarily reflected in the incorporation of different nonlinear functions into the network. Das et al. proposed a multi-reference active noise control framework based on the Functional Link Artificial Neural Network (FLANN) to address the challenge of multi-source active control in nonlinear acoustic noise processes. By employing trigonometric function expansion, FLANN enhances nonlinear fitting capabilities while avoiding the computational burden associated with hidden layers in multilayer neural networks (MLANN) [15]. Patra and Kot introduced an improved FLANN structure called the Chebyshev Functional Link Artificial Neural Network (CFLANN). This method offers the advantage of maintaining dynamic system identification accuracy while overcoming the heavy computational load of traditional MLPs and addressing the lack of noise robustness validation in existing FLANN structures [16].
Fig. 3Internal structure of the functional link neural network
George and Panda proposed an innovative cascaded adaptive nonlinear filter structure, termed CLFLANN (Cascaded FLANN and Legendre). The core idea of this method is to cascade a FLANN filter with a Legendre Polynomial Network (LeNN), thereby combining the strengths of both architectures: the FLANN provides rich nonlinear mapping capabilities at the front end through trigonometric function, while the LeNN performs further nonlinear approximation at the back end using computationally efficient Legendre polynomials. This hybrid structure effectively addresses the performance and efficiency bottlenecks faced by existing single-structure NANC methods (such as the high computations of FLANN and the potentially limited representational power of LeNN) when dealing with complex nonlinear noise [17]. Zhao et al. proposed an adaptive FLANN filter based on convex combination, aiming to overcome the performance limitations caused by fixed step sizes in single FLANN filters. The approach runs two independent adaptive FLANN filters in parallel: one with a large step size for fast convergence, and the other with a small step size for low steady-state error. By using a dynamically adjusted convex combination parameter to blend the outputs of the two filters, the proposed algorithm simultaneously optimizes convergence speed and steady-state accuracy [18]. Luo et al. addressed the issue of coefficient dependency in the nonlinear parts of FLANN filters by inserting a correction filter before the trigonometric expansion, thereby enhancing the handling of cross terms [19]. Le et al. proposed a Generalized Exponential Function-Link Artificial Neural Network with Channel-Reduced Diagonal structure (GE-FLANN-CRD) filter. By introducing appropriate cross terms and adaptive exponential factors within the trigonometric expansion, this filter improves nonlinear processing capability in nonlinear active noise control (NANC) [20]. Kukde et al. proposed an Incremental Learning-based Adaptive Exponential Function-Link Network (AE-FLN) approach, a distributed active noise control method that addresses the challenges of existing centralized schemes (such as Volterra series and FLANN) which suffer from performance degradation caused by nonlinear acoustic paths (NPP/NSP) and excessive computational/communication overhead in large-scale deployments [21]. Yin et al. introduced a family of adaptive algorithms based on a Hermite Polynomial-based FLANN (HFLANN) and the Fractional Lower Order Moment (FLOM) criterion. This approach effectively addresses challenges faced by existing neural ANC (NANC) methods in Internet of Vehicles (IoV) scenarios, such as sensitivity to impulsive noise, high computational complexity, and limited structural flexibility [22]. Mylonas et al. proposed an innovative framework that couples a mixed-error second-order Functional Link Neural Network (FLNN) with first-order sound pressure prediction. Designed with a lightweight architecture, the framework overcomes challenges such as nonlinear acoustic path suppression and silent zone localization. It reduces computational cost by 36 % while improving harmonic attenuation at 48 Hz from 1 dB to 17 dB using the FxLMS algorithm [23].
Table 3Summary of functional link artificial neural network
Innovations | Specific Operations | Advantages |
Linking Trigonometric Polynomial Functions | Expands input signals into a set of trigonometric-related functions and combines them with weight vectors | Enhances signal representation capability |
Linking Chebyshev Polynomials | Applies Chebyshev polynomial functional expansion to inputs | Eliminates the need for hidden layers in MLPs, simplifying the network structure |
Linking Legendre Polynomials | Used as an expansion module in FLANNs and cascaded with FLANN filters | Low computational complexity |
Adaptive Fuzzy Feedback Neural Network (AFFNNC) Controller | Combines two FLANN filters with different step sizes | Suitable for low-frequency nonlinear noise |
Combined Scheme Based on Adaptive Function-Link FLANN Filters | Inserts a correction filter before trigonometric expansion and splits nonlinear coefficients into two parts | Effectively handles cross terms, reduces coefficient dependency, and lowers computational complexity |
IFLANN and SIFLANN Filters | Introduces appropriate cross terms and adaptive exponential factors into trigonometric expansions | Suitable for strongly nonlinear environments and varying secondary path characteristics |
Generalized Exponential Function-Link FLANN | Uses adaptive exponential functions for functional expansion of the reference signal | Applicable to large-scale, complex spatial noise control scenarios |
Adaptive Exponential Function-Link Network (AE-FLN) | Combines with a recurrent structure; filter output is fed back and expanded using Hermite polynomials | Suitable for dynamically changing noise environments |
FLANN Based on Hermite Polynomials | Expands input signals using trigonometric functions to enhance nonlinear acoustic processing capabilities | Effectively handles low-frequency noise; advantageous in reducing sound pressure and attenuating harmonics |
Second-Order Trigonometric Function-Expanded FLNN | Utilizes symmetry in cross terms and reasonably adds cross terms to first-order FLANN | Higher accuracy than traditional FLANN |
q-Gradient-Based FLANN Filter | Introduces q-gradient into the FLANN framework | Suitable for handling abrupt noise |
Laguerre-Based FLNN Filter | Approximates long primary paths using truncated Laguerre series, reducing filter length | Suitable for NANC systems with long impulse response primary paths |
Le and Mai. proposed an Efficiently Extended Functional Link Artificial Neural Network (EE-FLANN) controller to address a critical bottleneck in the application of Generalized Functional Link Artificial Neural Networks (GFLANNs): the rapid increase in computational complexity – scaling quadratically with the input memory length – when handling memory nonlinearities in nonlinear active noise control. By employing a symmetric cross-term truncation technique and a data-dependent partial update algorithm, EE-FLANN significantly reduces computational complexity by over 20 %, while maintaining noise suppression performance comparable to GFLANN in terms of NMSE metrics [24]. Zhu and Zhao et al. proposed a filter based on Laguerre Function Link Neural Networks (Laguerre-FLNNs) along with a corresponding Information-Theoretic Learning (ITL) adaptive algorithm. This method addresses two major challenges faced by traditional Functional Link Neural Networks (FLNNs) in handling long-impulse-response nonlinear active noise control (NANC) systems: the high computational burden caused by the use of Finite Impulse Response (FIR) filter structures, and the sharp performance degradation in non-Gaussian impulsive noise environments. By employing Laguerre series orthogonal basis functions to approximate the system’s dynamic characteristics, the method significantly reduces the required filter length. In addition, it incorporates entropy-based criteria and an online vector quantization (VQ) technique to maintain robustness comparable to complex ITL algorithms, while reducing computational complexity to a level close to that of lightweight Minimum Correntropy Criterion (MCC) algorithms. Ultimately, the proposed method achieves a well-balanced performance in complex scenarios involving long acoustic paths, strong nonlinearities, and impulsive noise – delivering outstanding noise reduction (ANR improved by 5-10 dB) and enhanced computational efficiency (MEE computation speed increased by a factor of four) [25]. To address the performance limitations of existing methods in impulsive noise environments and nonlinear path scenarios, Yin et al. proposed a q-gradient-based Functional Link Artificial Neural Network (FLANN) filtering method. By reconstructing gradient computation using Jackson derivatives, the approach significantly amplifies the gradient magnitude, thereby accelerating convergence and suppressing impulsive interference. Moreover, a time-varying q-strategy is introduced to dynamically adjust the gradient step size: large q-values are used during the initial phase to speed up convergence, while smaller -values are applied in the steady state to reduce residual error [26].
3.3. Hidden layer improvements
In terms of hidden layer improvements, current trends focus on enhancing the precision of noise signal control, improving the accuracy of weight vector prediction, and accelerating convergence speed. Additionally, some studies have proposed innovative combinations of convolutional neural networks with fuzzy neural networks, indicating that neural network architectures will not be limited to recurrent networks but will integrate with other types of network structures Table 4 shows the summary of hidden layer improvements
Leng et al. proposed an optimization method for secondary path identification based on BP neural networks. This method addresses the limitations of traditional Finite Impulse Response (FIR) models, which struggle to accurately represent nonlinear factors in the secondary path, leading to insufficient modeling accuracy and reduced control performance [27]. Huynh and Chang introduced a Nonlinear Adaptive Feedback Neural Controller (NAFNC). The innovation of this approach lies in its use of a three-layer feedback neural network structure combined with an online learning mechanism, which overcomes the issues of offline training and slow convergence commonly seen in early neural network controllers [28]. Wu et al. proposed a multi-channel ANC algorithm based on a decoupled PID neural network, solving the dilemma in multi-channel ANC systems where nonlinear coupling and real-time performance cannot be simultaneously achieved [29]. Cha et al. designed a deep learning feedback ANC algorithm named DNoiseNet, which integrates causal convolutional layers, dilated convolution modules, RNNs, and fully connected layers. Through the collaboration of these modules, the algorithm effectively extracts noise features and generates anti-noise signals. Experiments demonstrate that this method achieves an average noise reduction of 23.30 dB on a dataset of 12 types of noise (including non-stationary construction noise and high-frequency aircraft noise), representing a 70 % performance improvement over baseline deep models such as LSTM, CNN, and RNN [30]. Li et al. proposed an error-free sensor active noise cancellation method based on Convolutional Fuzzy Neural Networks (C-FNN). This method employs convolutional neural networks (CNNs) to extract noise signal features and fit virtual error signals, addressing issues found in other methods such as weak feature extraction and poor convergence stability. The fuzzy neural network (FNN) adaptively adjusts filter weight coefficients [31]. Luo et al. introduced the GFANC-Bayes and GFANC-Kalman methods to address critical shortcomings of Selective Fixed Filter ANC (SFANC). Luo proposed the GFANC-Bayes and GFANC-Kalman methods to address critical shortcomings of Selective Fixed Filter ANC (SFANC). Traditional SFANC relies on a limited number of pre-trained control filters, which leads to a sharp decline in noise reduction performance when the input noise differs significantly from the training noise (such as dynamic traffic noise or aircraft noise in real scenarios. These methods employ a 1D CNN to predict the combination weights of sub-control filters. By incorporating Bayesian filtering and Kalman filtering, they improve the accuracy and robustness of weight vector prediction while maintaining low computational complexity [32], [33].
Table 4Summary of hidden layer improvements
Innovations | Specific operations | Advantages |
Single Hidden Layer BP Neural Network Structure | Replaces the traditional FIR filter structure with a single hidden layer BP neural network identifying the secondary path | Improves the accuracy of secondary path modeling |
Three-Layer Perceptron Feedback Neural Network | Combines feedback components with adaptive weights by adjusting parameter α and bias parameter B; and updates weights using the FXLMS algorithm | Eliminates the need for pre-training the neural network |
PID-based Neural Network | Uses the nonlinear characteristics of the PID neural network to adjust ANC system control parameters | Suitable for multi-channel noise control and addresses coupling between channels |
Deep Learning Feedback ANC | Incorporates causal convolution layers, dilated convolution modules, RNN, and fully connected layers working together | Integrates multiple advanced components, effectively captures multi-level temporal noise features, and reduces computational cost |
Attention-based Recurrent Network (ARN) | Embeds an attention mechanism layer component | Enhances the feature selection capability of CNNs |
Convolutional Fuzzy Neural Network (C-FNN) | Uses the translation invariance of convolutional layers to extract and model noise signal features, estimating a virtual error signal | Suitable for scenarios where sensor installation is difficult |
GFANC-Bayes and GFANC-Kalman Methods | Uses 1D CNN to predict the combination weights of sub-control filters, with the filtering module determining the final combination weights based on both prior and predicted information. | Pre-trainable broadband control filter is decomposed into multiple sub-control filters, which are adaptively combined |
Singh et al. proposed an attention-based convolutional neural network (CNN) for ANC, aiming to address performance bottlenecks faced by traditional adaptive filters (such as the FxLMS algorithm) and existing deep learning ANC models in nonlinear distortion scenarios (especially speaker saturation effects). While conventional methods can handle linear noise, they lack robustness against nonlinear distortion; and although standard CNN models can learn complex mapping relationships, they struggle to dynamically focus on critical acoustic features. The proposed approach embeds an attention layer to enhance the CNN’s feature selection capability, enabling the model to adaptively focus on key spatiotemporal noise patterns, and combines piecewise linear functions to explicitly compensate for hardware nonlinearity [34]. Zhang et al. developed a time-domain Attention Recurrent Network (ARN) architecture that combines delay compensation training with a revised Overlap-Add (OLA) method to achieve a zero-latency deep ANC system overcoming causal constraints. This study addresses two core challenges with systematic solutions: 1) To tackle the high latency caused by frequency-domain methods requiring long frame lengths (> 20 ms) for frequency resolution, they designed a time-domain ARN processing framework that maintains excellent noise reduction performance even with ultra-short frame lengths (4 ms), achieving a 2.06 dB improvement in NMSE over frequency-domain CRN models; 2) To overcome the performance limitations of adaptive filtering (e.g., FxLMS) in nonlinear distortion environments, they employed an end-to-end ARN to directly model speaker nonlinear characteristics, significantly enhancing robustness. Experimental results demonstrate that the ARN’s noise prediction capability (compensating a 15 ms delay with only a 0.95 dB performance loss) combined with the optimized frame processing of the revised OLA method ultimately achieves a negative algorithmic delay of –2 ms, with performance degradation controlled within 0.47 dB [35].
4. Improvements in training methods
Improvements in training methods can be categorized into three parts: first, loss functions; second, weight update algorithms; and third, others.
4.1. Loss function
The loss functions listed below can enhance noise reduction performance under different noise environments while also reducing computational complexity. It is essential to select them flexibly based on the application context of the algorithm. Table 5 presents various loss functions used in such algorithms and their respective advantages.
Table 5Summary of loss functions
Loss function | Specific form | Advantages |
Based on mean squared error | Applicable in most scenarios | |
Based on weighted cumulative mean squared error | Uses variable momentum factor to improve traditional LMS algorithm | |
Defined by the Fractional Lower Order Moment (FLOM) criterion | Overcomes amplitude bursts caused by impulsive signals in traditional MSE | |
Mean squared error loss function with a forgetting factor | Forgetting Factor | Focuses on recent data influence |
Based on the Maximum Correntropy Criterion (MCC) | Improves computational efficiency | |
Frequency-domain Loss Function Defined by the Euclidean distance between the ideal and generated anti-noise signals | Measures error from frequency domain perspective, reducing computational complexity |
Most neural network-based ANC algorithms adopt Eq. (1) as the loss function:
In a hybrid narrowband active noise control (HNANC) system under multi-noise environments, Padhi et al. introduced a modified loss function Eq. (2):
where, represents the purely feedforward-correlated noise component separated from the total error. This loss function, which precisely targets the relevant error, significantly improves the convergence accuracy of the feedforward path [36]. Yin et al. defined the loss function Eq. (3) based on the Fractional Lower Order Moment (FLOM) criterion:
The functions above can effectively enhance the algorithm’s robustness and convergence performance when dealing with non-Gaussian noise and nonlinear systems [22]. Shi et al. introduced Eq. (4) as the loss function:
with a forgetting factor for Model-Agnostic Meta-Learning (MAML) by incorporating a forgetting factor into the traditional mean squared error function. This approach forces the optimizer to focus on the transient convergence phase during system initialization, significantly shortening the transition time for adaptive algorithms to reach stable noise reduction[37]. Zhu et al. proposed the Fractional-order Ascending Maximum Mixed-Correntropy Criterion (FAMMCC) algorithm, which applies correntropy to Functional Link Artificial Neural Networks (FLANNs) for nonlinear active noise control. The loss function is represented as Eq. (5):
The loss function maximizes correntropy to optimize filter parameters. This approach outperforms traditional algorithms in handling non-Gaussian noise and enhances adaptability to complex noise environments [38], [25]. Jiang et al. introduced a frequency-domain loss function defined by the Euclidean distance between the ideal and generated anti-noise signals, which is represented as Eq. (6):
Compared to time-domain MSE, this formulation better matches the acoustic characteristics and avoids the need for phase alignment, while significantly reducing computational complexity [39].
The loss functions listed above serve different purposes – some are designed to enhance noise reduction performance under varying noise environments, while others aim to reduce computational complexity. It is important to select them flexibly based on the specific application context of the algorithm.
4.2. Weight update algorithms
Improvements in weight update algorithms primarily aim to reduce computational complexity, enhance the accuracy of weight control, accelerate convergence speed, overcome suboptimal solutions, and improve the generalization capability of the neural network model. Table 6 summarizes the advancements in weight update algorithms.
Zhou et al. proposed a weight update algorithm based on SPSA, which requires only two measurements of the loss function to obtain an approximate gradient. This allows for simultaneous updating of all weights in the RFNN, greatly simplifying the derivation process of the adaptive weight algorithm and completely avoiding the need for differentiating the secondary path, thereby accelerating the training speed of the neural network [40]. Bambang proposed a nonlinear active noise control method using recursive fuzzy neural networks based on Kalman filtering. By combining the Extended Kalman Filter (EKF) with the Adjoint Method, this approach addresses the bottleneck of gradient computation lag and convergence efficiency in real-time adaptive control of dynamic nonlinear systems [41].
Table 6Summary of training methods
Training Methods | Specific Operations | Advantages |
SPSA Algorithm | Generates perturbation vectors and perform two evaluations of the error function to approximate the virtual gradient | No need for secondary path modeling |
Recursive Fuzzy Neural Network based on Kalman Filtering | Adjusts RFNN weights using EKF algorithm with instantaneous gradients and Kalman gain | Improves weight control accuracy and convergence speed |
Adaptive Learning Rate Adjustment based on Immune Feedback Law | Analogizes T-cell regulation mechanism from biological immune system to neural network training | Adjusts learning rate via immune feedback law, accelerating convergence and avoiding local minima |
Neural Network Training based on Genetic Algorithm (GA) | Uses real-valued encoding, roulette wheel selection, heuristic crossover, and uniform mutation combined with MSE function for parameter tuning | Overcomes suboptimal solutions of traditional gradient backpropagation in multimodal cost functions |
Firefly Algorithm | Optimizes weight parameters by simulating attraction and movement among fireflies | Simple and general, with parameters flexibly adjustable according to application context |
Improved Model-Agnostic Meta-Learning (MAML) algorithm | Obtains the initial weights of the control filter by training on multiple noise samples to find initial control filter that can quickly adapt to noise with varying amplitudes | Trains across multiple related tasks to enable rapid parameter adaptation to new tasks |
Optimized Decision Feedback (ODF-FLANN) architecture | Real-time learning rate adjustment based on residual noise | Automatically corrects learning rate, reducing computational burden |
Bayesian Regularization (trainbr) algorithm based on the Levenberg–Marquardt method | Automatically adjusts regularization parameters and step-size factors in Levenberg-Marquardt algorithm | Strong generalization ability of the network |
Adaptive Labeling Mechanism | Converts weight vectors into data labels | Reduces manual workload |
Sasaki et al. proposed an adaptive learning rate neural network algorithm incorporating an immune feedback law, aiming to improve noise control performance and reduce training time. This algorithm introduces the feedback mechanism of the immune system into the learning rate adjustment of the neural network: when the weight change trend is stable, the learning rate is increased (to accelerate convergence); when the change oscillates, the learning rate is decreased (to avoid divergence) [42]. Krukowicz employed Genetic Algorithm (GA) to train neural networks, effectively overcoming the issue where traditional gradient-based backpropagation (BP) algorithms may converge to suboptimal solutions in multimodal cost functions [43]. Walia and Ghosh proposed an Active Noise Control (ANC) system that optimizes the weights of a hybrid Functional Link Artificial Neural Network (FLANN) and Finite Impulse Response (FIR) filter using the Firefly Algorithm (FA). Their approach addresses two major challenges in nonlinear ANC systems: the tendency of gradient-based optimization to gradient-based optimization to get trapped in local convergence and the premature convergence of heuristic algorithms [44]. Shi et al. introduced an improved Model-Agnostic Meta-Learning (MAML) algorithm, which incorporates a forgetting-weighted loss function and first-order approximate gradient updates. The proposed MAML algorithm generates initial control filter weights with generalization ability, fundamentally resolving the contradiction between computational efficiency and scenario adaptability in traditional methods [37]. Liang et al. proposed the Optimized Decision Feedback-FLANN (ODF-FLANN) structure based on the traditional Functional Link Artificial Neural Network (FLANN), addressing the issues of delayed convergence or even divergence in conventional fixed learning rate algorithms when faced with sudden noise changes [45]. Leng et al. employed the Bayesian Regularization algorithm (trainbr) based on the Levenberg-Marquardt algorithm to train the weights of each layer in a BP neural network, enhancing the network’s generalization ability [27]. Luo et al. proposed an adaptive labeling mechanism that minimizes the error signal using the LMS algorithm to obtain an optimal weight vector, which is then converted into a binary weight vector serving as labels for the training noise. This enables automatic labeling of the training dataset and reduces manual workload [46]. The training algorithms listed above each have distinct advantages in handling complex noise signals and should be applied according to specific application scenarios.
4.3. Other training methods
Wuraola and Patel proposed a criterion-based small-batch noise injection method to accelerate the convergence of neural network training. This method adaptively adjusts the level of noise injected into the network weights during training based on criteria such as absolute error and error variation rate, thereby avoiding the pitfalls of local minima [47]. Zhang and Wang introduced a deep ANC framework that, for the first time, reformulates active noise control as a supervised learning task. By incorporating a physically embedded loss function and a dual-modality training strategy, the framework addresses the performance degradation problem of traditional methods under strong nonlinear distortion [48]. Luo et al. proposed a novel unsupervised learning method for training 1D convolutional neural networks (1D CNNs) in GFANC systems. By integrating the coprocessor and real-time controller into an end-to-end differentiable ANC system, and using cumulative squared error signals as the loss to update network parameters, this approach eliminates the need for labeled data, reduces training costs, and mitigates labeling bias, while achieving strong noise reduction performance in real noise experiments [49]. Luo et al. further proposed a CNN-based zero-latency selective fixed-filter active noise control method (CNN-SFANC), which combines neural networks with adaptive filtering. This algorithm utilizes a neural network model with only 0.25M parameters, working in tandem with the filter, making it suitable for real-time hardware deployment. It achieves zero-latency noise cancellation and can effectively cope with dynamically changing noise [50].
5. Conclusions
Active Noise Control (ANC) technology plays a crucial role in improving acoustic environments. However, the widespread presence of nonlinear factors in real applications – such as noise source saturation, abrupt changes in acoustic paths, and actuator nonlinearity – severely limits the performance of traditional linear adaptive algorithms, such as the FxLMS algorithm. Neural network-based ANC algorithms, with their powerful nonlinear mapping capabilities and universal approximation properties, offer a highly promising solution to this fundamental challenge. By constructing complex nonlinear functional relationships, neural networks can effectively model the nonlinear processes involved in noise generation, propagation, and cancellation. This leads to significantly improved noise reduction performance and system robustness in complex noise environments, making neural network-based approaches a key direction for overcoming the limitations of traditional ANC technologies.
5.1. Summary
This paper systematically reviews the research progress of neural network-based ANC algorithms, with a focus on two core aspects: network architectures and training methods.
At the network structure level, innovations are mainly reflected in topological structure innovations, various Functional Link Artificial Neural Networks (FLANNs), and the deep optimization of hidden layers. Innovations in topological structures, such as the introduction of recurrent mechanisms, endow models with the temporal dependency and memory capabilities required to handle time-varying noise. However, these enhancements come at the cost of increased training complexity and reduced real-time performance due to the structural complexity. FLANN offers the advantage of structural simplicity and typically lower computational complexity compared to multilayer perceptrons (MLPs). By introducing functional expansions, it gains nonlinear capabilities and are relatively easy to deploy on hardware. Nevertheless, its expressive power is constrained by the choice and order of the basis functions used. The deep optimization of hidden layers is primarily achieved through the introduction of deep neural networks, which enable end-to-end learning of complex mappings thanks to their powerful feature extraction and nonlinear modeling capabilities. This approach is well-suited for complex scenarios but typically requires the support of a large amount of training data.
At the training method level, innovations primarily focus on the optimization design of loss functions and the diversification of weight update algorithms. Research on the loss function has moved beyond the limitations of traditional Mean Squared Error (MSE), proposing various improved solutions tailored to specific noise characteristics and system requirements. For example, loss functions defined directly in the frequency domain better align with acoustic properties, help mitigate phase alignment issues, and reduce computational burden. The core objective of the weight update algorithm is to address the bottleneck in gradient computation, enhance convergence speed and accuracy, and avoid local optima. Representative progress includes the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm, which eliminate reliance on secondary path models and their derivatives, significantly simplifying the online training process for complex networks. Meanwhile, other efficient training strategies are also being continuously explored. Although significant progress has been made, current research still faces a prominent contradiction between theory and application: although training paradigms can deliver superior performance, their high computational cost makes it difficult to meet the real-time constraints of embedded devices. Meanwhile, lightweight methods (such as approximate gradient strategies) are often limited by insufficient convergence accuracy and weakened generalization capability. More critically, existing training mechanisms still heavily rely on offline pre-training or idealized assumptions. They lack adaptability to uncontrollable dynamic factors in open environments, such as sudden noise bursts, time-varying acoustic paths, and actuator nonlinear drift. As a result, these algorithms often suffer performance degradation when applied in actual deployment. It is imperative that future research resolves these conflicts by exploring computationally efficient and highly adaptive training mechanisms, thereby advancing neural network-based ANC technology from theoretical advantages toward broader practical applications.
5.2. Future research directions
Based on the summary of current research and the challenges faced, and in light of recent advances in the field of artificial intelligence, future studies on neural network-based ANC can focus on the following key directions:
1) Efficient and Lightweight Network Architectures: Develop more computationally efficient and compact specialized network architectures (such as applying techniques model pruning, quantization, and knowledge distillation to ANC networks) to meet the stringent resource constraints of embedded devices and real-time systems; explore the potential of the novel and efficient architectures (such as Transformer and State Space Model (SSM)) in modeling long-range noise dependencies, striking a better balance between noise suppression performance and computational complexity; and design adaptive network architectures capable of dynamically adjusting model complexity and resource consumption in response to real-time noise characteristics.
2) More Robust and Adaptive Training Strategies: Develop more efficient online learning and meta-learning algorithms that enable neural networks to rapidly adapt to unknown noise source characteristics, time-varying acoustic paths (such as those caused by opening/closing doors and windows or human movement), and nonlinear hardware features (e.g., speaker aging); explore the application potential of unsupervised and self-supervised learning paradigms in ANC to reduce dependence on large amounts of labeled data (e.g., high-precision error signals).
3) Hardware-Friendly Algorithms and Deployment: Optimize neural network models and training algorithms based on the characteristics of specific hardware platforms (such as DSPs and FPGAs); develop dedicated neural network parameter compression and speedup techniques to promote the deployment of high-performance neural network-based ANC in practical applications such as industrial equipment and consumer electronics.
In summary, neural network-based ANC algorithms demonstrate tremendous potential in addressing the challenges of nonlinear noise control. With continued advances in neural network theory, optimization algorithms, and computing hardware, along with the integration of domain-specific knowledge and emerging AI technologies, this field is poised to achieve breakthroughs in algorithm performance, computational efficiency, system robustness, and engineering applicability. These developments will provide more effective active noise reduction solutions for a wider range of real applications.
References
-
N. V. George and G. Panda, “Advances in active noise control: A survey, with emphasis on recent nonlinear techniques,” Signal Processing, Vol. 93, No. 2, pp. 363–377, Feb. 2013, https://doi.org/10.1016/j.sigpro.2012.08.013
-
K.-A. Chen, Active Noise Control. China: National Defense Industry Press, 2014.
-
M. O. Tokhi and R. Wood, “Active noise control using multi-layered perceptron neural networks,” Journal of Low Frequency Noise, Vibration and Active Control, Vol. 16, No. 2, pp. 109–144, Jun. 1997, https://doi.org/10.1177/026309239701600204
-
M. O. Tokhi and R. Wood, “Active noise control using radial basis function networks,” Control Engineering Practice, Vol. 5, No. 9, pp. 1311–1322, Sep. 1997, https://doi.org/10.1016/s0967-0661(97)84370-5
-
M. O. Tokhi and S. M. Veres, “Intelligent adaptive active control of noise and vibration,” IFAC Proceedings Volumes, Vol. 32, No. 2, pp. 8740–8745, Jul. 1999, https://doi.org/10.1016/s1474-6670(17)57491-1
-
Z. Qizhi and J. Yongle, “Active noise feedback control using a neural network,” Shock and Vibration, Vol. 8, No. 1, pp. 15–19, Sep. 2000, https://doi.org/10.1155/2001/604583
-
Y. Zhou, Q. Zhang, X. Li, and W. Gan, “Model-free control of a nonlinear ANC system with a SPSA-based neural network controller,” in Lecture Notes in Computer Science, Berlin, Heidelberg: Springer Berlin Heidelberg, 2006, pp. 1033–1038, https://doi.org/10.1007/11760023_152
-
Q.-Z. Zhang and W.-S. Gan, “Active noise control using a simplified fuzzy neural network,” Journal of Sound and Vibration, Vol. 272, No. 1-2, pp. 437–449, Apr. 2004, https://doi.org/10.1016/s0022-460x(03)00742-9
-
Q.-Z. Zhang, W.-S. Gan, and Y.-L. Zhou, “Adaptive recurrent fuzzy neural networks for active noise control,” Journal of Sound and Vibration, Vol. 296, No. 4-5, pp. 935–948, Oct. 2006, https://doi.org/10.1016/j.jsv.2006.03.020
-
X. Guo, J. Jiang, L. Tan, and S. Du, “Improved adaptive recursive even mirror Fourier nonlinear filter for nonlinear active noise control,” Applied Acoustics, Vol. 146, pp. 310–319, Mar. 2019, https://doi.org/10.1016/j.apacoust.2018.11.022
-
M.-C. Huynh and C.-Y. Chang, “Novel adaptive fuzzy feedback neural network controller for narrowband active noise control system,” IEEE Access, Vol. 10, pp. 41740–41747, Jan. 2022, https://doi.org/10.1109/access.2022.3167402
-
H. Zhang and D. Wang, “Deep ANC: A deep learning approach to active noise control,” Neural Networks, Vol. 141, pp. 1–10, Sep. 2021, https://doi.org/10.1016/j.neunet.2021.03.037
-
S. Zhang, X. Liang, L. Shi, L. Yan, and J. Tang, “Research on narrowband line spectrum noise control method based on nearest neighbor filter and BP neural network feedback mechanism,” Sound and Vibration, Vol. 57, pp. 29–44, Jan. 2023, https://doi.org/10.32604/sv.2023.041350
-
S. Juang, L. Cao, H. Guo, Y. Wang, Y. Tao, and N. Liu, “A nonlinear noise active control algorithm based on deep neural network,” Noise Control Engineering Journal, Vol. 72, No. 4, pp. 337–346, Jul. 2024, https://doi.org/10.3397/1/377224
-
D. P. Das, G. Panda, and S. Sabat, “Development of FLANN based multireference active noise controllers for nonlinear acoustic noise processes,” in Lecture Notes in Computer Science, Berlin, Heidelberg: Springer Berlin Heidelberg, 2004, pp. 1198–1203, https://doi.org/10.1007/978-3-540-30499-9_186
-
J. C. Patra and A. C. Kot, “Nonlinear dynamic system identification using Chebyshev functional link artificial neural networks,” IEEE Transactions on Systems, Man and Cybernetics, Part B (Cybernetics), Vol. 32, No. 4, pp. 505–511, Aug. 2002, https://doi.org/10.1109/tsmcb.2002.1018769
-
N. V. George and G. Panda, “Active control of nonlinear noise processes using cascaded adaptive nonlinear filter,” Applied Acoustics, Vol. 74, No. 1, pp. 217–222, Jan. 2013, https://doi.org/10.1016/j.apacoust.2012.07.002
-
H. Zhao, X. Zeng, Z. He, S. Yu, and B. Chen, “Improved functional link artificial neural network via convex combination for nonlinear active noise control,” Applied Soft Computing, Vol. 42, pp. 351–359, May 2016, https://doi.org/10.1016/j.asoc.2016.01.051
-
L. Luo, Z. Bai, W. Zhu, and J. Sun, “Improved functional link artificial neural network filters for nonlinear active noise control,” Applied Acoustics, Vol. 135, pp. 111–123, Jun. 2018, https://doi.org/10.1016/j.apacoust.2018.01.021
-
D. C. Le, J. Zhang, D. Li, and S. Zhang, “A generalized exponential functional link artificial neural networks filter with channel-reduced diagonal structure for nonlinear active noise control,” Applied Acoustics, Vol. 139, pp. 174–181, Oct. 2018, https://doi.org/10.1016/j.apacoust.2018.04.020
-
R. Kukde, M. S. Manikandan, and G. Panda, “Incremental learning based adaptive filter for nonlinear distributed active noise control system,” IEEE Open Journal of Signal Processing, Vol. 1, pp. 1–13, Jan. 2020, https://doi.org/10.1109/ojsp.2020.2975768
-
K.-L. Yin, Y.-F. Pu, and L. Lu, “Hermite functional link artificial-neural-network-assisted adaptive algorithms for IoV nonlinear active noise control,” IEEE Internet of Things Journal, Vol. 7, No. 9, pp. 8372–8383, Sep. 2020, https://doi.org/10.1109/jiot.2020.2989761
-
D. Mylonas, A. Erspamer, C. Yiakopoulos, and I. Antoniadis, “A virtual sensing active noise control system based on a functional link neural network for an aircraft seat headrest,” Journal of Vibration Engineering and Technologies, Vol. 12, No. 3, pp. 3857–3872, Aug. 2023, https://doi.org/10.1007/s42417-023-01090-5
-
D. Cong Le and T. Anh Mai, “Efficient implementation of the functional links artificial neural networks with cross-terms for nonlinear active noise control,” International Journal of Electrical and Computer Engineering (IJECE), Vol. 14, No. 4, p. 3922, Aug. 2024, https://doi.org/10.11591/ijece.v14i4.pp3922-3930
-
Y. Zhu, H. Zhao, S. S. Bhattacharjee, and M. G. Christensen, “Quantized information-theoretic learning based Laguerre functional linked neural networks for nonlinear active noise control,” Mechanical Systems and Signal Processing, Vol. 213, p. 111348, May 2024, https://doi.org/10.1016/j.ymssp.2024.111348
-
K. Yin, H. Zhao, and L. Lu, “Functional link artificial neural network filter based on the q-gradient for nonlinear active noise control,” Journal of Sound and Vibration, Vol. 435, pp. 205–217, Nov. 2018, https://doi.org/10.1016/j.jsv.2018.08.015
-
C. Leng, D. Wang, and S. Zhou, “Optimization of secondary path identification in active noise control based on neural network,” (in Chinese), Journal of East China University of Science and Technology (Natural Science Edition), No. 6, pp. 761–768, Dec. 2021, https://doi.org/10.14135/j.cnki.1006-3080.20200928001
-
M.-C. Huynh and C.-Y. Chang, “Nonlinear neural system for active noise controller to reduce narrowband noise,” Mathematical Problems in Engineering, Vol. 2021, pp. 1–10, May 2021, https://doi.org/10.1155/2021/5555054
-
X. Wu, Y. Wang, H. Guo, T. Yuan, P. Sun, and L. Zheng, “A decoupling algorithm based on PID neural network for multi-channel active noise control of nonstationary noise,” The International Journal of Acoustics and Vibration, Vol. 27, No. 2, pp. 91–99, Jun. 2022, https://doi.org/10.20855/ijav.2022.27.21835
-
Y.-J. Cha, A. Mostafavi, and S. S. Benipal, “DNoiseNet: Deep learning-based feedback active noise control in various noisy environments,” Engineering Applications of Artificial Intelligence, Vol. 121, p. 105971, May 2023, https://doi.org/10.1016/j.engappai.2023.105971
-
T. Li et al., “A convolutional fuzzy neural network active noise cancellation approach without error sensors for autonomous rail rapid transit,” Processes, Vol. 11, No. 9, p. 2576, Aug. 2023, https://doi.org/10.3390/pr11092576
-
Z. Luo, D. Shi, X. Shen, J. Ji, and W.-S. Gan, “GFANC-Kalman: generative fixed-filter active noise control with CNN-Kalman filtering,” IEEE Signal Processing Letters, Vol. 31, pp. 276–280, Jan. 2024, https://doi.org/10.1109/lsp.2023.3334695
-
Z. Luo, D. Shi, W.-S. Gan, and Q. Huang, “Delayless generative fixed-filter active noise control based on deep learning and Bayesian filter,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, Vol. 32, pp. 1048–1060, Jan. 2024, https://doi.org/10.1109/taslp.2023.3337632
-
D. Singh, R. Gupta, A. Kumar, and R. Bahl, “Attention based convolutional neural network for active noise control,” in ICMLSC 2024: 2024 The 8th International Conference on Machine Learning and Soft Computing, pp. 122–126, Jan. 2024, https://doi.org/10.1145/3647750.3647769
-
H. Zhang, A. Pandey, and L. Wang, “Low-latency active noise control using attentive recurrent network,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, Vol. 31, pp. 1114–1123, Jan. 2023, https://doi.org/10.1109/taslp.2023.3244528
-
T. Padhi, M. Chandra, A. Kar, and M. N. S. Swamy, “A new adaptive control strategy for hybrid narrowband active noise control systems in a multi-noise environment,” Applied Acoustics, Vol. 146, pp. 355–367, Mar. 2019, https://doi.org/10.1016/j.apacoust.2018.11.034
-
D. Shi, W.-S. Gan, B. Lam, and K. Ooi, “Fast adaptive active noise control based on modified model-agnostic meta-learning algorithm,” IEEE Signal Processing Letters, Vol. 28, pp. 593–597, Jan. 2021, https://doi.org/10.1109/lsp.2021.3064756
-
Y. Zhu, H. Zhao, and P. Song, “Fractional-order ascent maximum mixture correntropy criterion for FLANNs based multi-channel nonlinear active noise control,” Journal of Sound and Vibration, Vol. 559, p. 117779, Sep. 2023, https://doi.org/10.1016/j.jsv.2023.117779
-
L. Jiang, H. Liu, L. Shi, and Y. Zhou, “A neural network assisted FuLMS algorithm for active noise control system,” in Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, Cham: Springer Nature Switzerland, 2024, pp. 412–427, https://doi.org/10.1007/978-3-031-67162-3_26
-
Q. Zhang, Y. Zhou, X. Liu, X. Li, and W. Gan, “A nonlinear ANC system with a SPSA-based recurrent fuzzy neural network controller,” in Lecture Notes in Computer Science, Berlin, Heidelberg: Springer Berlin Heidelberg, 2007, pp. 176–182, https://doi.org/10.1007/978-3-540-72383-7_22
-
R. T. Bambang, “Nonlinear active noise control using EKF-based recurrent fuzzy neural networks,” International Journal of Hybrid Intelligent Systems, Vol. 4, No. 4, pp. 255–267, Dec. 2007, https://doi.org/10.3233/his-2007-4405
-
M. Sasaki, T. Kuribayashi, S. Ito, and Y. Inoue, “Active random noise control using adaptive learning rate neural networks with an immune feedback law,” International Journal of Applied Electromagnetics and Mechanics, Vol. 36, No. 1-2, pp. 29–39, Feb. 2011, https://doi.org/10.3233/jae-2011-1341
-
T. Krukowicz, “Neural fixed-parameter active noise controller for variable frequency tonal noise,” Neurocomputing, Vol. 121, pp. 387–391, Dec. 2013, https://doi.org/10.1016/j.neucom.2013.05.007
-
R. Walia and S. Ghosh, “Design of active noise control system using hybrid functional link artificial neural network and finite impulse response filters,” Neural Computing and Applications, Vol. 32, No. 7, pp. 2257–2266, Sep. 2018, https://doi.org/10.1007/s00521-018-3697-5
-
K. H. Liang, W. D. Weng, and T. A. Chang, “Design of self-adaptive optimized decision feedback functional link artificial neural network based active noise controller,” International Journal of Electrical Energy, Vol. 22, No. 5, Jan. 2015, https://doi.org/10.6329/ciee.2015.5.02
-
Z. Luo, D. Shi, X. Shen, J. Ji, and W.-S. Gan, “Deep generative fixed-filter active noise control,” in ICASSP 2023 – 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1–5, Jun. 2023, https://doi.org/10.1109/icassp49357.2023.10095205
-
A. Wuraola and N. Patel, “Stochasticity-assisted training in artificial neural network,” in Lecture Notes in Computer Science, Cham: Springer International Publishing, 2018, pp. 591–602, https://doi.org/10.1007/978-3-030-04179-3_52
-
H. Zhang and D. Wang, “A deep learning approach to active noise control,” in Interspeech 2020, pp. 1141–1145, Oct. 2020, https://doi.org/10.21437/interspeech.2020-1768
-
Z. Luo, D. Shi, X. Shen, and W.-S. Gan, “Unsupervised learning based end-to-end delayless generative fixed-filter active noise control,” in ICASSP 2024 – 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 441–445, Apr. 2024, https://doi.org/10.1109/icassp48485.2024.10448277
-
Z. Luo, D. Shi, J. Ji, X. Shen, and W.-S. Gan, “Real-time implementation and explainable AI analysis of delayless CNN-based selective fixed-filter active noise control,” Mechanical Systems and Signal Processing, Vol. 214, p. 111364, May 2024, https://doi.org/10.1016/j.ymssp.2024.111364
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Ruoqin Liu: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing-original draft preparation, visualization. Qichao Liu: methodology, software, validation. Yunhao Wang: software, writing-review and editing. Wenjing Yu: supervision, project administration, funding acquisition. Guo Cheng: conceptualization, methodology, resources, writing-review and editing, supervision, project administration, funding acquisition.
The authors declare that they have no conflict of interest.
