Abstract
This paper presents an integrative review of control strategies in robotics, covering classical control methods (linear quadratic regulator, proportional-integral-derivative), modern methods (adaptive, sliding mode, model predictive, and H-infinity), intelligent control methods (neural network, fuzzy logic, and machine learning), and hybrid control methods (integration of classical, modern, and intelligent control methods) to identify the advantages, limitations and gaps for future. A brief comparison of control methods between the types of control strategies is conducted with respect to robustness, stability, and complexity of implementation on 3 different levels of evaluation criteria: high, average, and low; advantages; limitations; and robotic applications, including examples. This paper discusses the theoretical and practical advancements and the classification of control strategies according to controller types (linear, nonlinear, and learning-based), approaches (model-based and model-free), and classifications (centralized, decentralized, and modal control). The review highlights the strengths, limitations, and potential research directions in bridging classical, modern, intelligent, and hybrid control paradigms to achieve safe, efficient, and adaptive robotic behavior in complex, uncertain environments. We discuss the future direction: autonomy, human-robot collaboration, and enhanced learning and challenges: cost, reliability, safety of control strategies, concluding with recommendations for future research.
Highlights
- Hybrid control strategies combining classical, modern, and intelligent methods provide superior performance compared to single control approaches in robotic systems with complex dynamics and uncertainties.
- Integration of machine learning with traditional control methods enhances adaptability and real-time decision-making capabilities while addressing stability limitations in autonomous robotic applications.
- Classical control methods remain widely used but are insufficient for nonlinear systems, while modern methods excel in handling uncertainties and disturbances.
- Intelligent control approaches offer model-free solutions for complex robotic tasks but face challenges in ensuring system stability and require significant computational resources.
- Future robotics development focuses on AI-enhanced control systems that enable autonomous learning, human-robot collaboration, and real-time adaptation to dynamic environments.
1. Introduction
The primary objective of the control system in modern Robotics is to minimize the product risks and costs based on the customer demands across academia, research, medicine, and industry sectors. The purpose of the control system of robotics is to implement the real-world robotics application (e.g., Robot Manipulator Control System, UAV Flight Control System, Autonomous Vehicle Control System, Medical Robots Control System) integrating hardware (sensors, actuators), control laws based on control strategies, and computation. As well as modern robotics, control strategy of robots is becoming the innovative point of all types of robots. The development and implementation of the new type of robotics is the main drive of Industry and other sectors using the innovative approaches based on the control strategies: classical, modern, intelligent and hybrid including the control methods to achieve higher efficiency and more desirable outcomes. Nowadays, Robotics faces difficulties to build the modern robots based on the linear and classical control strategies. In addition, the artificial intelligent system has gradually increased in recent years in the field of robotics.
The main aim of the control strategies is a high-level approach or philosophy guiding control design using control methods based on the types of controllers. The control strategies define the overall framework used to control a system, such as whether it relies on feedback, optimization, or machine learning activities. Control methods are specific techniques under the control strategy that dictate how control is applied and describe the general mathematical approach that how control is regulated include stability, robustness and optimization based on their simplicity or complexity.
The invention of the new type of robot is more complex and requires the development of the various control algorithms which are interconnected with existing algorithms and integration of intelligent system elements. That’s why modern robots have very complex structures, and their control algorithms involve the specific computational and implementation procedure, formulas and programs in real-world environments. In [1, 30], the effective way of developing the control algorithm analyzed more effectively as a hybrid and artificial intelligent-based control algorithm. Hence the control algorithm may be considered as a description (mathematical model) of the controller.
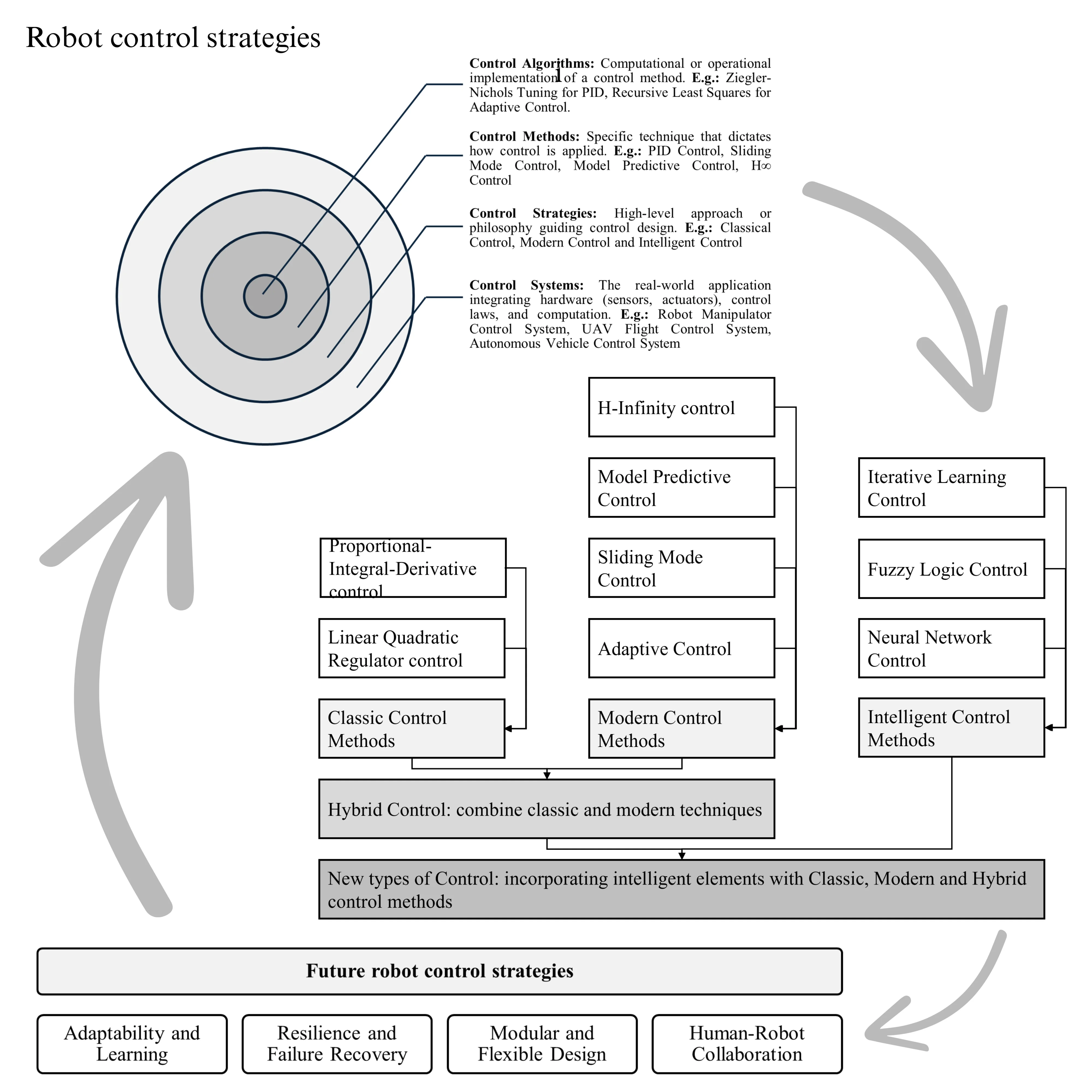
In Fig. 1, the main keywords of this article are defined and explained more clearly and shown the interconnection.
Fig. 1Definition, mutual differentiation and coherence of the main keywords: control algorithm, control method, control strategy and control system
In this article we analyze the control strategies including control methods advantages, limitations and their effectiveness in robotics applications, prepare the recommendations on the possibilities of future use in a hybrid and integrated manners. The aim of this paper is to provide an integrative review of the various control strategies developed for robot systems. Addressing the challenges faced by robots and other factors influencing their performance, a thorough examination of different control strategies is presented, detailing the advantages and disadvantages of each approach. Innovative technical solutions are highlighted to ensure optimal performance in various tasks and operating conditions. In addition, several research issues are identified that require further investigation. Finally, current advances in robots for research and commercial applications are discussed and suggestions for their control strategies are developed.
1.1. Structure of the paper
The paper structure consists of 6 sections. In Section 2, Fundamentals of control strategies include methods presenting mathematical equations with structure scheme, advantages, limitations and the main key features. In Section 3, the classification of Control methods as linear, nonlinear, and learning based control based on control techniques, and approaches: model-based and model-free types as a method and classification of control strategies as centralized, decentralized and modal control are reviewed. Sections 4 and 5 contain the performance metrics of control strategies, comparative analysis of control methods, and hybridization in the practical implementation of control strategies. At the end, in Section 6, the concluding remarks and recommendations for future research are stated.
1.2. Research and paper selection methodology
The integrative review research papers on robotic control strategies are sourced papers from MDPI, IEEE Xplore, CrossRef and ResearchGate database in English language. The searching methodology for papers is based on the keywords: “Control strategy in Robotics” and “Reviewed paper on control strategies”. The selecting methodology focuses on methods of control strategies, implementation and design of new methods in Robotics, and innovative approach of control system in Robotics.
2. Fundamentals of control strategies in robotics
This section reviewed the types of control strategies based on the control methods. All works and analyses in this paper applied on the rigid-body robots including rigid links connected by joints.
Robots are the more effective and higher costly device in the industry and medical sector. In Medical area, robots are used as surgical robotics, rehabilitation robotics, and prosthetic devices [1, 35]. Different types of robots are utilized based on customer needs and requirements. They can be categorized according to various criteria, including Degree of Freedom, Kinematic Structure, Dynamics of Control, Drive Technology, Sensing System, Workspace Geometry, Motion System, and Control Strategy. The main controlled parameters of robots are the position, velocity, and acceleration of the links that are determined based on the joint angles and forces [2].
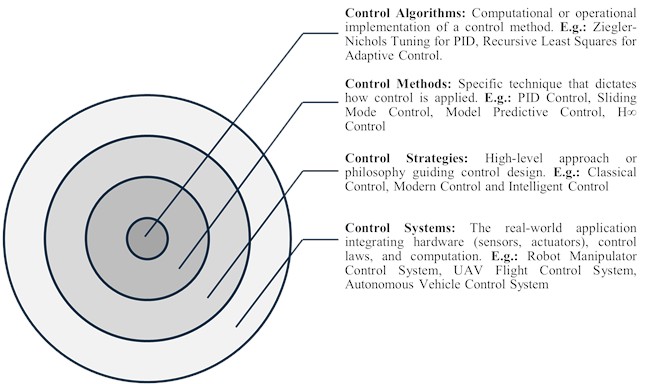
Fig. 2Classification of control strategies in robotics based on methods: classic control, modern control, intelligent control, hybrid control and new types of control methods
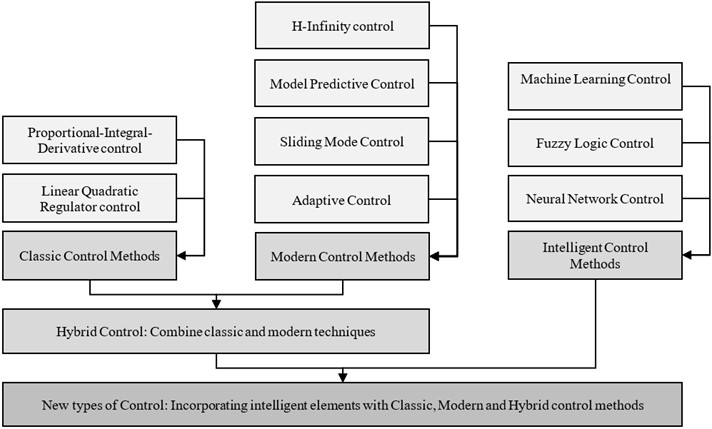
Control strategy of the robot control system is one of the main items to develop the technological process. The effective application of the control strategy depends on the control methods. There are three types of control strategies: classical control strategy, modern control strategy and intelligent control strategy. In previous research papers, hybrid control strategy is also one of the types of control strategy, shaped from synergetic integration of classical and modern type. In Fig. 2, the types of control strategies including methods which reviewed in this paper, hybrid control strategies which are formed by using classical and modern methods in conjunction with each other and new types of control strategy which are created by applying the intelligent elements to classical, modern and hybrid methods are shown. In the approach to types of control strategies in robotics, the concepts of control strategy, control method, control algorithm, and control system are widely used, but there are some differences between them. In this section, control strategies mainly based on control methods are analyzed. This classification helps differentiate between broad approaches (strategies), specific techniques (methods), computational implementations (algorithms), and real-world applications (systems).
2.1. Classic control methods
Classic control methods are the basis of modern control and intelligent control theory and studies of linear systems. It is suitable for SISO: single input, single output, solving the analysis of systems and optimization problems [1]. Classical control methods consist of two main methods: proportional integral derivative control (PID) and linear quadratic regulator control (LQR) methods. These kinds of methods offer robust performance and effective control for linear industrial robots and are more effective to ensure the reliability and stability of the system. Implementation of the control in these methods is much easier than others. Table 1 presents the key features of classical methods based on the three main components: robustness, stability and complexity of implementation on 3 different levels of evaluation criteria: high, average and low, advantages, limitations and robotic applications including the examples.
Table 1Comparison of classical control methods in robotics
Types, references | Definition | Key features | Advantages | Limitations | Robotics applications |
PID control, [1]-[4], [8]-[12], [16], [17], [22], [23], [26], [55] | This method adjusts the control input based on the error, set point, and output | Robustness: Low. Stability: High. Complexity: Low. | – It is simple for implementation and well-modeled systems. – It is easy to choose the gain. | – It is poor robustness for nonlinear systems and disturbances. – It cannot predict the future errors. – It is difficult to tune for complex plants. | It is mostly used in industrial manipulators, stabilizing robotic joint positions and motion planning. |
LQR control, [2], [4], [9], [11], [17], [26], [29], [55] | This method optimizes the control input to minimize a quadratic cost function | Robustness: High. Stability: Low. Complexity: Average. | – It is optimal for performance. – It is one of the best methods for minimal control energy usage. – It has a MIMO compatibility. – It offers a fast response, and it is easy to design. | – It required full-state feedback. – It needs accurate system modeling. | It is widely used in Robotic arms, legged robots, humanoid control, autonomous navigation. |
PID control method is used in industrial automation widely, although it requires complex systems, performance improvement and disturbance immunity. PID controllers are the most used in the control system because they are easy to design and implement, clarity of functionality and adaptability [1]. In the other hand, utilization of the error between the desired and actual position or state to adjust the control commands are most used in the control systems [4]. The main advantages of PID control are to improve stability, guarantee product quality and to maximize product efficiency in different sectors using the real-world examples [22]. There are some limitations due to the non-linearity in technological procedures, PID control struggles to achieve ideal results. Moreover, parameter tuning methods are complex, making it difficult to set conventional PID controller parameters without adaptive tuning. These limitations restrict PID control applications in robotics [23]. On the other hand, PID control method is one of the most error deviation and major energy consumption [27].
The PID control consists of three components. The PID components are linear. PID combines proportional, integral, and derivative components [22]. The proportional component reduces the error based on proportional method. If the proportional () gain value is too low, the support signal may be inadequate to compensate for interference effects. The integral component eliminates residual error and relies on the cumulative sum of the uncertainties. If the integral () gain is higher, it can lead to overshoot due to accumulated past errors. The derivative component reduces the rate of change of error. The derivative () gains predict future values based on control error, enhancing system stability and tuning time.
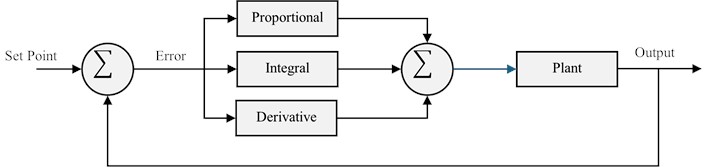
The PID controller has an algorithm block diagram given in Fig. 3. The output of the PID control algorithm is shown in the Eq. (1). This algorithm adjusts the control input based on the error, set point, and output:
where, is system error.
Fig. 3PID control technique
Using AI for PID parameter tuning improves adaptability of the systems. By integration of PID controller with fuzzy logic or neural network controller, the system will be optimized the structure and parameters. In another way, the metaheuristic algorithm can achieve optimal performance and can be assisted in designing the nonlinear PID controller [25].
Linear Quadratic Regulator (LQR) control is based on the feedback strategy for using the optimization of minimizing the cost function, which reflects system performance, including error and control effort. LQP is a classical control method, and the main purpose is to optimal state-feedback based on state-space theory, optimization principles and MIMO: multiple input and multiple output, capable designs. It can manage complex systems as a MIMO, but LQR control method demands and requires an accurate system model.
In the other hand, LQR control method is based on the optimal control techniques and in some papers, it uses optimal control methods instead of LQR control methods for nonlinear systems. In general, Optimal control application commonly uses the LQR in vibration suppression [26].
The main advantages of the LQR control method are the most efficient regulating multi-variable system with minimal energy use for MIMO systems [27]. However, request for perfect system modeling and linear assumptions, and incompatibility for nonlinear systems are the main limitations of the LQR control methods. In this regard, LQR is ensuring robust control performance based on the model-based controller [28]. LQR control methods are well-known methods for solution of the control forces for linear systems to ensure stability and robustness, providing the controllable system [29].
LQR algorithm optimizes the control input to minimize a quadratic cost function. LQR control utilizes a state-feedback control law and represents the control law is given as , where and satisfies the Riccati equation . The Ricotti Equation helps to calculate the optimal state-feedback gain for optimal control techniques. The Linear Quadratic Regulator (LQR) method formulates a linear state feedback control law as described in Eq. (2):
where, and present a -dimensional state vector, -dimensional output vector, is an -dimensional control vector. The control law aims to minimize the quadratic performance index (cost function) given in Eq. (3):
where, and are the weight matrix. The matrix influences state trajectory deviation and the matrix is related to the control quantity and actuator saturation.
Fig. 4LQR control technique
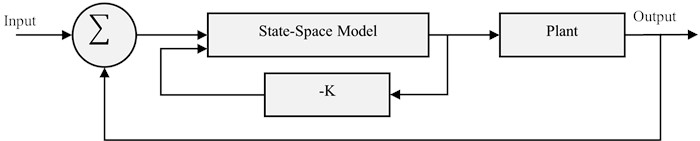
The LQR control method is suitable for minimizing the quadratic cost function that balances the state error and control effort under the small uncertainty and distribution in the linear MIMO system. Integrating with PID, Fuzzy Logic, Adaptive and Neural Network control methods, it can achieve the performances of nonlinear system on robustness, adaptability and human-like behavior.
2.2. Modern control methods
Modern control theory starts to be used in the 1950s and 1960 to address the limitation of classical control strategies, which is inadequate for MIMO nonlinear systems [1]. The principles of optimal control, dynamic programming, Kalman filter, and state space description have contributed to the widespread adoption of MIMO control. In recent decades, advancements in modern control methods such as Adaptive Control, Sliding Mode Control (SMC), H-infinity (H∞), and Model Predictive Control (MPC) have been successfully implemented across various industrial processes as sophisticated non-linear control systems. In Table 2, the key features of modern control methods based on the three main components: robustness, stability and complexity of implementation on 3 different levels of evaluation criteria: high, average and low, its advantages, limitations and robotic applications including the examples are shown.
Adaptive control methods are a modern control for dynamically adjust controller parameters to handle parameter uncertainty and external perturbations in robotic systems. Under unknown or changing dynamics, allowing the robotic arm to maintain stable trajectory tracking performance despite varying loads, friction forces, and external disturbances the adaptive control methods modify control parameters [1]. Robots operate in various environments to perform tasks and encounter uncertain environmental conditions. Adaptive control methods excel in managing complex systems with uncertainty, nonlinearity, and time-varying traits through continuous learning and self-optimization, ensuring robustness and efficiency in dynamic environments [34]. Adaptive control faces challenges in ensuring system stability, managing complexity, and reducing computational costs. It requires advanced hardware and software for real-time data processing, and tuning adaptation parameters must balance speed, accuracy, robustness, and sensitivity to noise and disturbances.
Table 2Comparison of modern control methods in robotics
Types, references | Definition | Key features | Advantages | Limitations | Robotics applications |
Adaptive Control [1], [2], [5]-[7], [9]-[12], [17], [31]-[34], [55] | This method adjusts its parameters in real-time to adapt to changing system dynamics | Robustness: High. Stability: Low. Complexity: High. | – Strong robustness vs. parameter variations. – Works for nonlinear systems. – Performs well when parameters change significantly and are difficult to model. | – Requires high computational resources. – Stability may be hard to guarantee. – Takes time to adapt with the parameters. | Robotic manipulators with varying payloads |
Sliding Mode Control [1], [2], [8], [9], [11], [12], [17], [23], [36]-[38], [55], [62] | This technique employs a non-continuous control signal to guide the system state towards a specified sliding surface. | Robustness: High. Stability: Low. Complexity: High. | – Robustness to Model Uncertainties. – Fast Response & Good Tracking Performance. – Effective Nonlinear & High-Degree-of-Freedom Systems. | – Difficult implementing design. – Sensitive to measuring noise. – Requires accurate system model. | Humanoid & Legged Robots, a specific class of wheeled robots |
H-infinity (H∞) control [1], [2], [8], [9], [11], [39], [42] | This method optimizes the control input to achieve robust performance in the presence of uncertainties | Robustness: High. Stability: Average. Complexity: High. | - High robustness. - MIMO compatibility. - Robustness to parameter changes and external disruptions. - Deals with system uncertainties. | - Complex design with uncertainties. - Complex to implement. - Requires complex controller structures. Performance trade-offs involved. | Manipulators, humanoid robots, mobile robots, cooperative robots. |
Model Predictive Control (MPC) [2], [4], [9], [11], [23], [34], [43], [46], [55], [62] | This approach employs a system model to forecast future behavior and optimize control inputs accordingly. | Robustness: High. Stability: Average. Complexity: High. | - Constraint satisfaction. - Predictive planning. - Real-time adaptability. - Suitability for multi-DoF robots. | - Computational complexity. - Sensitivity to model accuracy. - Potential delays in high-speed applications. | Manipulators, mobile robots, and human-robot interaction. |
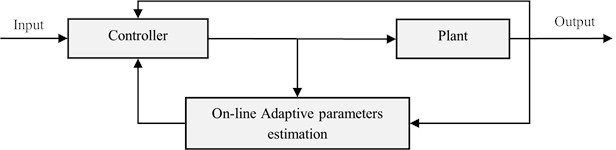
Adaptive controller’s parameters adjust automatically to accommodate the changing characteristics of the system being controlled or to account for initial uncertainties. Fig. 5 shows an optimal technique of adaptive control methods based on adaptive algorithm generates direct estimates of the controller’s parameters.
The adaptive controller is derived from the system's mathematical model, represented in the Eq. (4) equation:
where, is the system state, is the control input, and are system matrices that depend on unknown parameters. This algorithm adjusts its parameters in real-time to adapt to changing system dynamics.
There are five methods for adjusting parameters: gain scheduling, dual control, auto-tuning, self-tuning control, and model reference [9]. Adaptive control methods are divided into model-based control algorithms and non-model-based algorithms. Model-based adaptive control requires knowledge of model parameters, and the main advantage allows the physical interpretation of the system’s behavior and can identify system’s parameters variations. Model-free based adaptive control eses fuzzy logic or neural networks. Its main advantages are handling nonlinearity, supporting parallel implementation, and tolerating system uncertainties [32].
Adaptive control is applicable across various fields, offering significant advantages such as high flexibility, strong robustness, and the ability to adjust automatically under varying operating conditions. This results in enhanced system performance, especially when developed using advanced methods like artificial intelligence, neural network control, and fuzzy logic control.
Fig. 5Adaptive control technique
Sliding Mode Control (SMC) is a well-known suitable powerful nonlinear control method for robotics, particularly when dealing with unknown disturbances and system uncertainties. Sliding Mode Control is commonly used in robotic manipulators, humanoid robots, and force-controlled systems for high-performance tracking and robustness. SMC involves designing a switching hyperplane to achieve the desired system dynamic. SMC is resilient to parameter changes and disruptions. Standard SMC design involves knowledge of uncertainty bound, which may be difficult to apply, and it generally employs conservative estimate and excessive gain [21]. It offers robustness and stability at the same time good transient performance [24]. SMC has several disadvantages: chattering which causes high-frequency oscillations in the input, sensitivity to noise when input signals are near zero and the complexity of calculating nonlinear equivalent dynamic formulations crucial for good performance.
The system state model is shown in the Eq. (5) equation:
where, is the system state vector, is a control input, is a known nonlinear function, and is an external perturbation. SLC algorithm uses a discontinuous control signal to drive the system state to a desired sliding surface.
Fig. 6Sliding mode control technique
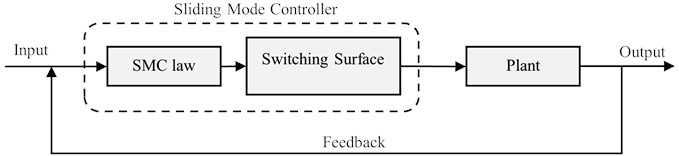
Designing the SMC involves creating a switching function that meets design criteria and selecting a control law to manage system states on the sliding manifold despite disturbances and uncertainties [38].
In general, sliding mode control is one of the best control of robots in nonlinear systems and this theory was initially proposed in the early 1950s by Emelyanov [38]. The traditional SMC evolved significantly in the mid-1980s with the introduction of the “second order sliding” concept. In the subsequent development phase during the 2000s, higher-order concepts gained considerable attention.
Recently, artificial intelligence methods have been applied to SMC systems. Neural networks control, fuzzy logic, and combination of neuro-fuzzy approaches have been integrated with sliding mode controllers and utilized in nonlinear, time-variant, and uncertain systems. Several researchers have developed an advanced and intelligent technique-based Sliding Mode Control (SMC) algorithm that effectively addresses systems with both structured and unstructured uncertainties. The integration of an observer with the SMC approach represents the latest advancement in sliding mode-based control systems.
H-Infinity control (H∞) is a well-known robust control method to optimize worst-case performance by minimizing the H∞ norm and to ensure strong robustness against system uncertainties and external disturbances. H∞ control is highly effective in managing uncertainty and nonlinear systems, as it can significantly suppress perturbations and ensure stable system performance. While applicable for vibration suppression in flexible connecting roads, the design and implementation process are complex and computationally intensive [1]. H-infinity control for robotic manipulators has been widely utilized in industrial applications, providing a solid theoretical foundation that can be applied to cooperative robotics [39]. The H-infinity is utilized to ensure performance and stability in the presence of internal uncertainties and external disturbances in mixed-sensitivity method, including sensor noise, unmodeled dynamics, and actuator control weight limitations [41]. It seeks to reduce the closed-loop effects of disturbances by optimizing the H∞ norm of a particular transfer function.
Advantages of the H∞ control are to provide a systematic approach to designing controllers that meet specific performance requirements, to ensure that the closed-loop system remains stable and performs well even in the presence of uncertainties and disturbances, and to allow for the design of controllers that can handle both structured and unstructured uncertainties. There are some disadvantages: complexity on computationally intensive, especially for high-order systems, conservatism on design process and on high-order controllers which may lead to large control effort requirements.
The H∞-based formulation of the robust control problem is shown in Fig. 7. Where is the vector of all perturbation signals, is the cost signal containing all errors, is the vector containing the measurement variables, and is the vector of all control variables [1].
Fig. 7H-infinity (H∞) control technique
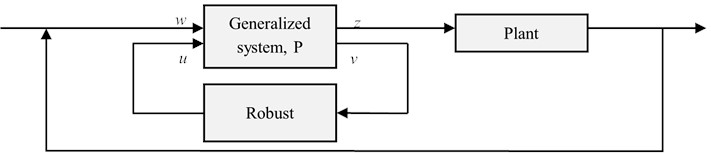
The generalized system as a has inputs, first one is an exogenous input includes reference signal and disturbances, second one is a manipulated variable . The first output is an error signals which require to minimize. Second output is a measured variables , which use to control the system. can be used in robust controllers as a to calculate the variables . Note that all these are generally vectors, while and are matrices. In formulae, the system is:
There are fundamentally two methodologies for H∞ system control design: mixed sensitivity and loop shaping design [41]. H∞ algorithm optimizes the control input to achieve robust performance in the presence of uncertainties. Integrating H-infinity control with AI in robotics focuses on developing control systems that can handle uncertainties and disturbances in real-world robotic applications. This method merges the robustness of H-infinity control with the learning capabilities of AI, allowing robots to perform tasks consistently and effectively.
Model Predictive Control (MPC) is based on a mathematical model for predicting the future system behavior and optimizing control commands. Model Predictive Control handles complex systems with constraints and disturbances effectively, but MPC requires an accurate system model and can be computationally demanding [4]. Model Predictive Control remains a critical control strategy in modern robotics, often hybridized with learning-based techniques for enhanced real-time decision-making. MPC is the nonlinear control system for supporting the predicts future states and errors of the system [9, 34]. Unlike classical control methods (e.g., PID, LQR), MPC explicitly incorporates system constraints and handles multi-input, multi-output (MIMO) systems natively, making it advantageous for complex robotic applications. Despite MPC’s broad use, implementing it on high degree of freedom systems demands significant computational power, limiting its application on embedded platforms [44]. It encounters challenges when handling complex, nonlinear processes. These challenges include the requirement for precise models, difficulty in adapting to process changes, and optimizing control actions.
MPC algorithm using a linear model has similar behavior. MPC algorithms can be used as models for predicting future behavior and optimize control inputs of the system:
where is step response, is the predicted output, is past output, and is the control law.
To compensate for the uncertainties of the model problem, an error term is added to the system output:
The correction term represents the differences between the actual output and the model’s output.
Fig. 8Model predictive control technique
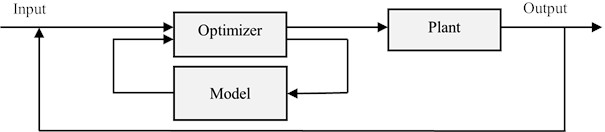
In conclusion, model predictive control is an effective approach for robot motion planning in intricate environments and used to generate online motion. By integrating dynamic models, optimization algorithms, and rolling optimization techniques, MPC can create secure and efficient trajectories while responding to environmental changes in real time [34, 44, 46].
Machine Learning Based MPC combines traditional MPC with machine learning. It uses ML algorithms for accurate system modeling, behavior prediction, and control action optimization. Key components are data collection, model training, and control optimization. Combining machine learning with MPC can greatly enhance control performance and efficiency.
2.3. Intelligent control methods
Classical and modern control theories face challenges with complex systems that don't fit accurate mathematical models. In the 1970s, Professor Fu Jingsun from Purdue university’s Electrical Engineering Department introduced intelligent control, combining artificial intelligence and automatic control into a new field [1]. Nowadays we can separate the robot system into 2 parts, the first is controlling robot system, and the second is intelligent system for robotics. Robot intelligence is based on intelligent control and involves understanding and identifying the external environment, which includes areas such as computer vision, voice processing, and natural language processing [5]. The intelligent control system's primary limitation was input point errors [17].
Table 3Comparison of intelligent control methods in robotics
Types, references | Definition | Key features | Advantages | Limitations | Robotics applications |
Fuzzy logic control [1], [2], [5], [9], [11], [16], [49]-[53], [62] | This method uses fuzzy logic to handle uncertainties and nonlinearities in the system | Robustness: Average. Stability: Average. Complexity: High. | – No Need for an Accurate Mathematical Model. – Works Well with Noisy or Incomplete Data. – Highly Flexible and Intuitive. – Adaptive to nonlinear and multivariable systems – Performs well in complex, uncertain environments. | – More complex fuzzy systems. – Less Effective for Highly Dynamic Systems. – Slow processing speed and low accuracy. – requires much time for tuning parameters. – Challenging to debug and optimize | Mobile robot navigation |
Neural Network Control [1], [2], [5], [7], [9], [11], [16], [49], [62] | This method uses neural networks to learn and optimize control inputs | Robustness: Average. Stability: Low. Complexity: High. | – Handles Nonlinearity and Uncertainty. – Refine control policies dynamically through experience. – Enables Learning from Data. – Identification of nonlinear systems. | – Requires large datasets for training and substantial computational resources for online learning. – Poor system stability. | Mobile robot path planning and navigation |
Machine Learning Control [11], [56]-[60] | This method uses machine learning techniques to improve control performance | Robustness: Average. Stability: Average. Complexity: High. | – Adaptability. – Improved Optimization & Performance. – Learning from Experience. – Hybrid Integration Potential. | – Lack of Formal Stability Guarantees. – Computational Complexity. – Requires large datasets or intensive simulations to train neural controllers. | Safety-Critical Robotics, Human-Robot Interaction, Autonomous vehicles, Space Robotics. |
Intelligent control in robotics uses AI techniques such as machine learning, neural networks, and fuzzy logic to help robots make decisions and adapt to complex environments, improving their autonomy and performance, while the system learns from past experience for improving the system performance [48]. Intelligent control methods solve the stability of the system, controller tuning, identification and optimization problems, and problems of iterative learning. In Table 3, the key features of intelligent control methods, their advantages, limitations and robotic applications including the examples are shown.
Future research for intelligent control methods aims to address the concept known as “learning-to-learn”, where the agent selects the learning strategy and adjusts its meta-parameters [48]. Additionally, advanced robotics is rapidly increasing based on advanced intelligent control. The trends include the use of intelligent control methods, multi-sensor fusion, and technologies like computer vision, VR & AR, remote control, adaptive sensor networks, human-robot interaction, and machine-to-machine interfaces [50].
Fuzzy logic control is an intelligent control method, that consists of fuzzy set theory, linguistic variables, and logic reasoning, applying fuzzy mathematics and theoretical control to actual controllers [1]. Fuzzy set theory, developed by Lotfi Zadeh in the 1960s, has been increasingly used for control applications in recent years. The fundamental principle of fuzzy logic, as opposed to Boolean logic, is its capability to handle computation with varying degrees of truth. From a theoretical perspective, it is possible to identify a nonlinear controller and model using a fuzzy rule base of logic, which serves as a “universal approximation”. Numerical samples, human expert data, and specific inputs/outputs data are sources that provide relevant system information for each device [49, 51].
Fuzzy control algorithms are capable of handling non-linear systems and do not require precise mathematical modelling. This algorithm uses fuzzy logic to handle uncertainties and nonlinearities in the system. Widely used in flexible robots, which often must deal with complex working environments and uncertainty, fuzzy control handles these variables and enhances the flexibility and adaptability of robot operation. Fuzzy control is used for robot path planning and obstacle avoidance in uncertain environments. By means of fuzzy rules, the robot can autonomously judge variables such as distance and speed, make appropriate decisions, and improve the intelligence and robustness of navigation [1], [16].
The FLC can be used in the non-linear system to support the robust controller for the uncertain, MIMO, and time-variant system model. The control system features fast response, short transient process, high precision, and good robustness [5]. A notable aspect of the fuzzy controller is its ability to implement expert knowledge linguistically and imitate human reasoning to manage complex systems [9].
Fig. 9Fuzzy logic control technique
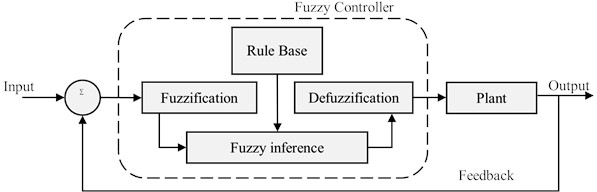
The fuzzy logic controller consists of four components: rule base, inference mechanism, fuzzification: determine inputs and outputs, converts the crisp inputs to fuzzy inputs; and defuzzification: transform fuzzy set to crisp set (Fig. 9). The center of gravity of the fuzzy set and output can be represented as:
where is the output membership function.
Fuzzy control rules are defined as follows:
1. If then ,
. If then ,
where , , is the linguistic value (fuzzy subset) vector corresponding to the language variable. The controller -dimensional input vector is . The control vector is t. is the fuzzy variable corresponding to .
FLC is used in industry, medicine and others relevant areas. The main limitation of this method is not ensuring the stability and acceptable performance of the system, but through integration with sliding mode controllers improves to reduce issues like chattering and to enhance system stability, which is a main challenge of FLCs.
Neural Network Control (NNC) is the intelligent control method inspired by the mammalian brain, which handles complex tasks like face recognition, body motion planning, and muscle activity control through billions of interconnected neurons. Throughout the 1940s, researchers focused on replicating the processes of the human brain and developed basic neuron software and device neurons. In the 1950s to 1960s, scientists created the first artificial neural network, which incorporated biological and surgical representations generated by McCulloch Pitts and other scientists [49, 54]. Key components of an NNC include the learning rule, activation function, neuron model, network architecture and training algorithm [11].
Neural network control utilizes artificial neural networks to model, approximate, or optimize control laws for robotic systems [1]. This approach has been extensively applied in the identification of nonlinear systems [5]. A neural network has a parallel structure that enables high-speed computation, fault tolerance, and real-time applications in robot manipulator control [7].
In robotics system, NNC is used mainly in controlling the robot system and identification. In this area, NNC is very effective on robot manipulators have uncertainty in dynamic part [1].
The design of NNC control is classified two stages: identification and design of controlling. Initially, the objective of system identification is to create a neural network model of the process that is regulated. Subsequently, this NNC model is employed to train the networks that are responsible for the system's control [16].
The output of the neural network can be represented as:
where is the output, is the activation function, is the weight matrix, is the input vector, and is the bias term. This algorithm uses neural networks to learn and optimize control inputs.
Fig. 10Neural network control technique
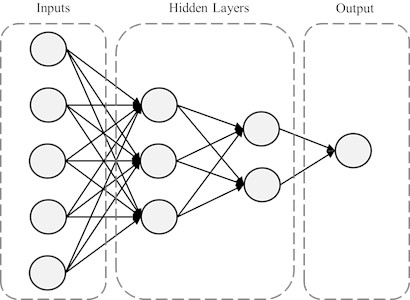
NNC model has three layers: input, hidden, and output (Fig. 10). Combining neural networks with other control methods, like fuzzy logic or traditional controllers like PID, enhances system performance and adapts to dynamic conditions. This hybrid approach leverages the strengths of each method, for example, combining the approximation capabilities of neural networks with the rule-based representation of fuzzy logic. Neural networks can also be used in conjunction with methods like MPC or SMC to improve robustness and accuracy, especially in complex systems with uncertainties [75].
Machine learning (ML) control is a creative adaptive system that learns from previous data and adjust to dynamic changes [11]. Machine learning control provides adaptability, self-learning abilities, and model-free execution, but it is constrained by high computational costs, lack of stability guarantees, and data inefficiencies. It is most effective in autonomous, nonlinear, and high-dimensional robotic tasks where conventional control struggles. Hybrid frameworks combining ML with traditional controllers help bridge reliability gaps, making ML-enhanced control a growing area of research.
Intelligent control offers robot manipulator controller designers an option. Due to uncertainty, real application sectors demand intelligent control strategies above traditional techniques [16]. ML control is a main part of intelligent control and aims to solve optimal control problems using machine learning methods. In machine learning control, a model is trained on a dataset to learn patterns. It is then tested on a separate test set to evaluate its performance and avoid overfitting. Feature engineering involves refining raw data into useful features to enhance model performance. In robotics, features include sensor readings and environmental parameters for accurate predictions. Model quality is assessed using performance metrics; classification tasks use accuracy, precision, recall, and score.
Combining machine learning with control systems advances autonomous robotics by enabling adaptation to dynamic and uncertain environments. Traditional control methods, relying on predefined models, work well in predictable settings but struggle in complex scenarios. Machine learning can learn from experience and data, enhancing robot decision-making and adaptability. This integration improves performance over time, handles uncertainties in sensor data, control parameters, and environment dynamics better than traditional methods.
Fig. 11Machine learning control technique
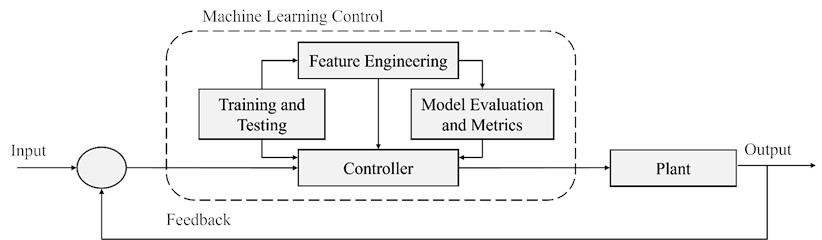
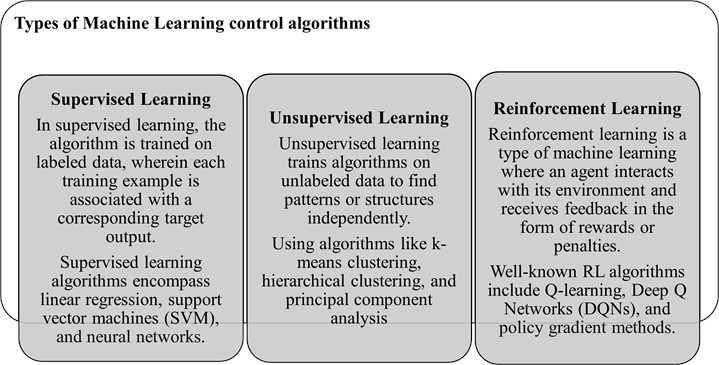
Machine learning improves robotic technologies and creates new opportunities across industries. Its adaptability, efficiency, and decision-making enhance robotic systems. Future research should refine these models for real-time use and address ethical issues to align advanced robotics with societal and industry needs [58]. In Fig. 12, the main algorithms of machine learning methods are shown and explained based on references: [56], [59], [60], and [65].
In general, Artificial Intelligent is the main elements of advanced robotics and to serve the development of following technologies for robotics: Object Recognition, Motion Planning, Control, Localization and Object Detection [61]. There is several programming languages utilized in robotics, including Python, C++, MATLAB, and ROS (Robot Operating System). These languages offer various libraries and tools that facilitate the integration of control strategies into robotic systems.
Fig. 12Types of machine learning control algorithms in robotics
3. Classification of control strategies
3.1. Linear, nonlinear and learning based controllers
In control strategies of robotics, the controllers are the main elements that is a device or algorithm for maintaining a process variable at a desired setpoint, even in the presence of disturbances or changes in the system. Controllers are classified into linear, nonlinear, and learning-based (Table 4).
Table 4Types of controllers in robotics
Controller type | Stability | Robustness | Implementation complexity |
Linear controllers [9], [11], [62] | High stability at nominal state | Low robustness except for H∞ | Less complex for implementation |
Nonlinear controllers [9], [11], [63] | Maintain system stability at nominal state | Good robust stability and acceptable performance | More complex but often perform better |
Learning-based controllers [14], [64-65] | Low stability under nominal conditions | Highly efficient in robust performance | More complex |
The LQR, PID and H∞ control methods are linear control techniques. Linear controllers are popular for experimental work due to their ease of implementation. Linear control methods are well-suited for systems that can be accurately represented by linear equations, making them easier to analyze and design. In robotics, linear control is often used for tasks such as trajectory tracking, position control, and stabilizing robot movements. Advantages of the linear control are simple to design and implement, making them suitable for various robotic applications, provide stable and predictable performance under certain conditions, and to be robust to certain types of disturbances and uncertainties. Limitations of linear control are linearity assumption, nonlinearities and disturbances.
Nonlinear control techniques often used are model predictive control, sliding mode, and adaptive controllers. Sliding mode control (SMC) is commonly used to manage various nonlinear systems. This method employs the switching and discontinuous nature of the control signal to modify the dynamics of the nonlinear system being managed [62]. Adaptive controllers are the most advanced nonlinear control schemes, aimed at estimating uncertain parameters and tuning the controller in real-time to adjust to dynamic variations in system parameters or environment [63].
Nonlinear control techniques offer advantages like handling complex system dynamics and achieving high performance without linearization, but also present limitations such as increased complexity and potential for instability.
Learning based control is developed in the mid-20th century in optimization theory, optimal control, and dynamic programming [64]. Learning-based controllers do not need precise dynamic models but rely on trials and flight data, including fuzzy logic, neural networks, and machine learning control [9]. The complexities, robustness and stability of robot control are important considerations. Both linear and nonlinear controllers can maintain system stability at the nominal state and ensure system performance. On the other hand, learning based controllers: fuzzy logic and neural networks cannot always guarantee stability, but can achieve high maneuvering performance. Linear controllers generally do not ensure system robustness except for H∞. MPC and adaptive controllers can ensure robustness and acceptable maneuvering performance among nonlinear controllers. Others provide robustness only in performance. Fuzzy and neural networks are inefficient in ensuring robustness for system maneuvering performance. In contrast, nonlinear and learning based controllers are more complex but often perform better [9], [11]. Nonlinear and learning based controllers are complex to design and implement, but they outperform linear controllers.
Learning based control techniques offer advantages such as adaptability to complex, dynamic environments and reduced reliance on precise system models, but also face limitations including high computational cost, potential instability, and the need for extensive training data.
3.2. Model-based and model-free approaches
In robotics, “model-based” and “model-free” describe two approaches to control strategies. Model-based methods use a learned or known model of the robot and environment to guide actions. Model-free methods learn directly from interactions without an explicit model.
Model-free control assumes that all joints are independent, resulting in individual controllers for each joint. Model-free methods do not require precise system models. These techniques use empirical data and learning algorithms to adjust to the robot's behavior in real-time. Examples of model-free control strategies include reinforcement learning, fuzzy logic control, and neural fuzzy control. These methods can address uncertainties but are computationally demanding and may need extensive training and tuning [66].
The model-based segment primarily compensates for the nonlinear systems and dynamics of the robotic system [14]. Model-based control approaches demand exact robot dynamics; hence controller effectiveness depends on robot mathematical model accuracy [18]. Model-based control involves designing controllers based on mathematical models that represent the robot’s dynamics and interactions with the environment. These models help predict the future state of the robot and allow for the computation of control actions that drive the robot its desired trajectory. Techniques such as LQR or MPC are often employed in this domain. While highly effective in structured and known environments, model-based control can struggle in dynamic and unpredictable settings, where real-time adjustments are critical.
Model-based methods are predictable and stable, whereas model-free methods are adaptable in uncertain environments. In general, admittance and impedance approaches of control system are totally suitable for model-based control methods [67].
In Table 5, the comparison of those approaches based on the model, adaptability, and complexity are indicated.
Model-free control differs from model-based control by not relying heavily on an accurate system model. This approach is useful when obtaining a precise model is difficult. In practical applications, model-based methods often suit simulation environments only. To overcome this limitation, model-free control was introduced, eliminating the need for model development and avoiding model uncertainties [67].
Table 5Comparison table of model-free and model-based
Type | Model | Adaptability | Complexity |
Model-free | Does not use a model | Can be more adaptable to changes in the environment | Can be simpler to implement |
Model-based | Uses a model of robot and environment | May be less adaptable to changes in the environment | Can be more complex to implement |
3.3. Centralized, decentralized and modal control
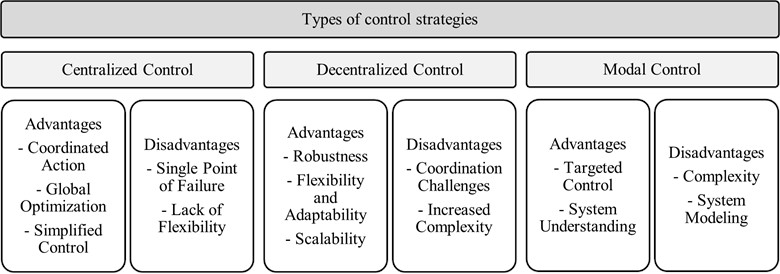
Typically, control strategies consist of centralized, decentralized and modal control types [26]. The centralized control is suitable for the dynamic model, and the multiple-input and multiple-output system, and all decisions and managements of system are controlled by one controller.
The transformation of MIMO into SISO based on inverse kinematics and dynamics model are the main elements of the decentralized control. In this type, each sub-system is controlled independently [26]. In a decentralized control system, multiple controllers make decisions independently, based on local information and interactions.
The modal control strategy, pioneered by Balas in the 1970s, offers robust stability for addressing unmodeled vibration modes. Modal control focuses on manipulating the system’s modes (eigenvalues) to achieve desired control objectives. The decoupling method is appropriate for the modal control strategy, which uses modal coordinates to reduce the vibrations of various primary modals [26].
Fig. 13Types of control strategies depending on the controller’s decision-making level
4. Performance metrics of control strategies
Key performance metrics of the control strategies include stability, which ensures the system remains in a desired state, robustness, which measures the system's ability to maintain performance despite uncertainties, and complexity, which assesses the ease of implementation and resource requirements. In robotics, stability refers to a robot’s ability to maintain its intended state or balance, robustness describes its capacity to function correctly despite uncertainties or disturbances, and complexity relates to the intricate nature of the robot’s design, algorithms, and tasks.
Robustness in robotics control refers to a control system's ability to maintain performance and stability even when faced with uncertainties, disturbances, and variations in the robot's environment or its own dynamics. It ensures the robot can continue functioning reliably despite these challenges.
Complexity in robotic control stems from the need to manage numerous interacting subsystems, including robot components, human interaction, and environmental interactions. This complexity manifests in characteristics like adaptation, self-organization, emergence, and the interaction of independent systems. To effectively control robots, systems must incorporate sensors, controllers, and actuators. Control methods like feedback control, which relies on continuous sensor feedback to adjust actuator movements, are crucial for maintaining accuracy and meeting performance targets, particularly in complex tasks [68].
In Table 6, the main concepts of the key performance metrics of control strategies for robotics are explained.
Table 6Key performance metrics of control strategies
Concepts | Stability | Robustness | Complexity |
Definition | Stability in robotics means a robot's ability to maintain its equilibrium and perform tasks without uncontrolled movements or oscillations | Robustness in robotics refers to a robot's ability to continue operating correctly even when faced with unexpected inputs, environmental changes, or sensor errors | Complexity in robotics refers to the intricacy of a robot's design, algorithms, and the tasks it performs |
Types | 1. Static stability: The ability to maintain balance while stationary 2. Dynamic stability: The ability to maintain balance and control while moving or performing tasks in a dynamic environment. | – | 1. Hardware: Complex robots may have many sensors, actuators, and control systems 2. Software: Complex robots may require sophisticated algorithms for perception, planning, and control 3. Tasks: Complex robots may be tasked with performing intricate or unpredictable operations |
Importance | Stability is crucial for robots to perform tasks reliably and safely, especially in dynamic or unpredictable environments | Robustness is essential for robots to function reliably in real-world scenarios where conditions are often unpredictable | Complexity is essential in design, development, and maintenance |
5. Comparison of control methods and Hybridization
Comparison of control methods entails systematically evaluating various control approaches to ascertain their strengths, weaknesses, and suitability for specific applications. This analysis facilitates the selection of the most effective control strategy by considering factors such as performance, complexity, and robustness.
PID control struggles with uncertainty and lacks robustness against interference [1]. While useful in some contexts, its application to robotic manipulators is limited by the inability to handle complex dynamics and varying conditions [2]. PID control, a linear algorithm, has a simple structure and low cost but requires parameter adjustments for different operating points. It assumes static system behavior; thus, control parameters fail when the system changes or if it is nonlinear without prior linearization. Consequently, PID control’s precision is inadequate for surgical robots dealing with nonlinear, time-delayed, or highly variable systems [23].
LQR requires a linear model to achieve an adequately controlled system, and it can manage multiple inputs and outputs simultaneously, unlike the PID controller. One disadvantage of LQR compared to PID is that it often results in steady-state error due to the absence of an integral component [9]. LQR is generally considered more robust than PID, especially when dealing with system uncertainties or disturbances. Comparatively, Model Predictive Control (MPC) offers advantages in handling non-linear systems and constraints by predicting future system behavior, potentially leading to better performance in some cases. Fuzzy logic controllers can also be used as an alternative to LQR, particularly in complex systems where traditional control methods may struggle [69].
Adaptive control performs better in terms of robustness and stability in changing environments, while sliding mode control is more robust to system uncertainty and has good stability in theory but produces jitter in practical applications thus affecting stability [1].
SMC is a nonlinear algorithm known for its robustness, enabling stable reach to the sliding surface as long as the system’s trajectory trend remains unchanged. However, it causes chattering, unlike PID and MPC [23]. SMC offers stability and robust performance in uncertain systems where PID fails [38], efficiently managing these systems and outperforming other techniques like H∞ and PID controllers [34].
MPC is a nonlinear control algorithm. Unlike PID control, MPC accounts for various constraints on spatial state variables, whereas PID only handles input and output constraints [23].
PID, adaptive, and fuzzy controllers are common in industry. Adaptive control adjusts the controller's structure and parameters based on changes in the control object or disturbances. PID controllers remain efficient and are now tuned using machine learning [48].
Hybrid control algorithms (Table 7) have emerged by combining the advantages of various methods and realizing the complementarity of their strengths and weaknesses. In the future, the application of robots is becoming more and more widespread, and the environmental factors they face are more variable and unknown, and hybrid control algorithms is widely used in robotic control system [1].
Table 7Examples of hybrid control methods
Hybrid control methods | Description | Advantages | References |
PID plus SMC | Model-free control approach | Better tracking performance than PID, comparable to standard SMC | [20] |
PID with MPC | Enhances accuracy in multivariable systems | Improves control accuracy | [20] |
Adaptive PID control | Optimize system responses in real-time | Improves robustness, adaptability, and resistance to disturbances | [34] |
Fuzzy PID control | Improves electrohydraulic position servo system | Enhances position tracking, suppresses external disturbances | [22] |
PID with neural networks | Adapts to complex, nonlinear systems | Improves control accuracy | [22] |
SMC with fuzzy neural network | Improves apple-harvesting manipulator's performance | Reduces sliding mode chattering, enhances control | [37] |
6. Future directions and open challenges in robotics control strategies
Robotics control will advance with greater autonomy, human-robot collaboration, and enhanced learning focusing on enabling robots to learn, adapt, and collaborate more effectively with humans, moving beyond simple automation towards more dynamic and intelligent systems. Developing adaptable robots involves resilient designs and learning-based control methods. Modular design and “plug and play” functionality will gain importance, alongside optimizing performance to reduce thermal and fatigue loads.
Fig. 14Future directions of robot control

The “Adaptability and Learning” in Fig. 14 as a main direction is formed based on control methods. In this direction, the main activities can learn from experience and adapt to changing environments in real-time, moving beyond pre-programmed tasks and learning optimal control policies based on feedback and observation for optimizing robot performance in dynamic and uncertain environments [70-74].
There are some issues on increasing the advantages of robotics control strategies as follows:
1) Integrating intelligence control with nonlinear control can enhance robotic adaptability.
2) New and improved sensors and actuators will necessitate the development of new control principles to utilize their capabilities effectively.
The issue of integrating AI with nonlinear control is the most suitable way for the future. AI-based robotic systems are a major focus due to their flexibility and advanced understanding of complex manufacturing processes, which enhance competitiveness [71]. AI integration into control systems is difficult. Numerous AI algorithms are computationally demanding, requiring substantial resources for training and real-time operation, which might restrict processing capacity for fast decision-making. Safety and reliability remain major concerns. AI may improve control performance, but important applications must be safe and adaptive. An AI system must be thoroughly evaluated and validated to handle unexpected situations and function securely [20].
Challenges include cost, reliability, safety, creating adaptable robots for dynamic environments, ensuring data security and privacy, and addressing ethical concerns in robot deployment. Additionally, integrating robots into existing systems, ensuring security and reliability, and addressing regulatory compliance are also major hurdles.
7. Conclusions
Robots have seen significant testing and development recently. Researchers continue to experiment with new designs, configurations, and control strategies for various applications. Robots will keep improving in safety, speed, size, strength, and intelligence [2]. Innovative solutions and new technologies are being developed on robots, mainly for use in academia, research, medicine, and industry. Overall, about 80 % of robots are for industrial purposes, while 5 % are for medical purposes.
Currently, a single type of robot control does not lead to good results. Hybrid control forms, through the integration of two or more control methods, provide an effective solution to such problems. In addition, the integration of artificial intelligence elements into hybrid control ensures that the control is perfect, effective, and most importantly, low-cost. Especially in the medical field, the need for these perfect control forms is very great.
In summary, the main challenges in robot control systems are achieving real-time control, singularity avoidance, adaptive control, human-robot interaction and incorporating advanced technologies such as Machine Learning and Artificial Intelligence. Future research in the field of robot control systems is likely to focus on addressing these challenges and incorporating advanced technologies to improve the performance, adaptability, and autonomy of the control systems [4].
In the future, the requirement to create a new environment of modern and perfect control will be how to separate the control function of hybrid and new type control, how to choose the control algorithms suitable for each link, how to switch between different algorithms, how to evaluate the stability, robustness and complexity of hybrid and new control methods. Our next scientific activity is the introduction and development of a new type of medical robot [35] based on machine learning control methods.
References
-
J. Wu, “A review of research on robot automatic control technology,” Applied and Computational Engineering, Vol. 120, No. 1, pp. 198–208, Jan. 2025, https://doi.org/10.54254/2755-2721/2025.19484
-
S. I. Abdelmaksoud, M. H. Al-Mola, G. E. M. Abro, and V. S. Asirvadam, “In-depth review of advanced control strategies and cutting-edge trends in robot manipulators: analyzing the latest developments and techniques,” IEEE Access, Vol. 12, pp. 47672–47701, Jan. 2024, https://doi.org/10.1109/access.2024.3383782
-
A.-D. Suarez-Gomez and A. A. H. Ortega, “Review of control algorithms for mobile robotics,” arXiv:2310.06006, Jan. 2023, https://doi.org/10.48550/arxiv.2310.06006
-
A. A. Ayazbai, G. Balbaev, and S. Orazalieva, “Manipulator control systems review,” Vestnik KazATK, Vol. 124, No. 1, pp. 245–253, Feb. 2023, https://doi.org/10.52167/1609-1817-2023-124-1-245-253
-
Q. Zhang, X. Sun, F. Tong, and H. Chen, “A review of intelligent control algorithms applied to robot motion control,” in IEEE 8th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), pp. 105–109, Jul. 2018, https://doi.org/10.1109/cyber.2018.8688124
-
C. Abdallah, P. Dorato, and M. Jamshidi, “Survey of the robust control of robots,” in American Control Conference, pp. 718–721, May 1990, https://doi.org/10.23919/acc.1990.4790827
-
M. J. Er, “Recent developments and futuristic trends in robot manipulator control,” in Asia-Pacific Workshop on Advances in Motion Control, pp. 106–111, Oct. 2024, https://doi.org/10.1109/apwam.1993.316198
-
H. G. Sage, M. F. de Mathelin, and E. Ostertag, “Robust control of robot manipulators: A survey,” International Journal of Control, Vol. 72, No. 16, pp. 1498–1522, Nov. 2010, https://doi.org/10.1080/002071799220137
-
R. Roy, M. Islam, N. Sadman, M. A. P. Mahmud, K. D. Gupta, and M. M. Ahsan, “A review on comparative remarks, performance evaluation and improvement strategies of quadrotor controllers,” Technologies, Vol. 9, No. 2, p. 37, May 2021, https://doi.org/10.3390/technologies9020037
-
T. Hsia, “Adaptive control of robot manipulators – a review,” in IEEE International Conference on Robotics and Automation, pp. 183–189, Jan. 1986, https://doi.org/10.1109/robot.1986.1087696
-
B. Singh, A. Kumar, and G. Kumar, “Comprehensive review of various control strategies for quadrotor unmanned aerial vehicles,” FME Transactions, Vol. 51, No. 3, pp. 298–317, Jan. 2023, https://doi.org/10.5937/fme2303298s
-
M. W. Spong, “An historical perspective on the control of robotic manipulators,” Annual Review of Control, Robotics, and Autonomous Systems, Vol. 5, No. 1, pp. 1–31, May 2022, https://doi.org/10.1146/annurev-control-042920-094829
-
A. T. Azar, Q. Zhu, A. Khamis, and D. Zhao, “Control design approaches for parallel robot manipulators: a review,” International Journal of Modelling, Identification and Control, Vol. 28, No. 3, p. 199, Jan. 2017, https://doi.org/10.1504/ijmic.2017.086563
-
D. Zhang and B. Wei, “A brief review and discussion on learning control of robotic manipulators,” in IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), pp. 1–6, Oct. 2017, https://doi.org/10.1109/iris.2017.8250089
-
A. Calanca, R. Muradore, and P. Fiorini, “A review of algorithms for compliant control of stiff and fixed-compliance robots,” IEEE/ASME Transactions on Mechatronics, Vol. 21, No. 2, pp. 613–624, Apr. 2016, https://doi.org/10.1109/tmech.2015.2465849
-
R. Kumar and K. Kumar, “Design and control of a two-link robotic manipulator: A review,” in 7th International Symposium on Negative Ions, Beams and Sources (NIBS 2020), Vol. 2373, p. 050020, Jan. 2021, https://doi.org/10.1063/5.0057931
-
P. Shukla and A. Kumar, “Comparative performance analysis of various control algorithms for quadrotor unmanned aerial vehicle system and future direction,” in International Conference on Electrical and Electronics Engineering (ICE3), pp. 498–501, Feb. 2020, https://doi.org/10.1109/ice348803.2020.9122868
-
S. Zein-Sabatto, J. Sztipanovitis, and G. E. Cook, “A multiple-control strategy for robot manipulators,” in IEEE Proceedings of the SOUTHEASTCON ’91, pp. 309–313, Sep. 2024, https://doi.org/10.1109/secon.1991.147762
-
E. M. Abdellatif, A. M. Hamouda, and M. A. Al Akkad, “Adjustable backstepping fuzzy controller for a 7 DOF anthropomorphic manipulator,” Intelligent Systems in Manufacturing, Vol. 22, No. 1, pp. 21–27, Mar. 2024, https://doi.org/10.22213/2410-9304-2024-1-21-27
-
H. Zhou, “A comprehensive review of artificial intelligence and machine learning in control theory,” Applied and Computational Engineering, Vol. 116, No. 1, pp. 43–48, Nov. 2024, https://doi.org/10.54254/2755-2721/116/20251755
-
P. R. Ouyang, J. Tang, W. H. Yue, and S. Jayasinghe, “Adaptive PD plus sliding mode control for robotic manipulator,” in IEEE International Conference on Advanced Intelligent Mechatronics (AIM), pp. 930–934, Jul. 2016, https://doi.org/10.1109/aim.2016.7576888
-
R. Chen, “A comprehensive analysis of PID control applications in automation systems: current trends and future directions,” Highlights in Science, Engineering and Technology, Vol. 97, pp. 126–132, May 2024, https://doi.org/10.54097/6q4xxg69
-
Y. Shi, S. Kumar Singh, and L. Yang, “Classical control strategies used in recent surgical robots,” in Journal of Physics: Conference Series, Vol. 1922, No. 1, p. 012010, May 2021, https://doi.org/10.1088/1742-6596/1922/1/012010
-
S. Kaur and G. Bawa, “Learning robotic skills through reinforcement learning,” in 3rd International Conference on Electronics and Sustainable Communication Systems (ICESC), pp. 903–908, Aug. 2022, https://doi.org/10.1109/icesc54411.2022.9885704
-
J. Li, “Analysis and comparison of different tuning method of PID control in robot manipulator,” Highlights in Science, Engineering and Technology, Vol. 71, pp. 28–36, Nov. 2023, https://doi.org/10.54097/hset.v71i.12373
-
Z. Yuan, Z. Zhang, L. Zeng, and X. Li, “Key technologies in active microvibration isolation systems: Modeling, sensing, actuation, and control algorithms,” Measurement, Vol. 222, p. 113658, Nov. 2023, https://doi.org/10.1016/j.measurement.2023.113658
-
D. A. Bravo M., C. F. Rengifo R., and J. F. Diaz O., “Comparative analysis between computed torque control, LQR control and PID control for a robotic bicycle,” in IEEE 4th Colombian Conference on Automatic Control (CCAC), pp. 1–6, Oct. 2019, https://doi.org/10.1109/ccac.2019.8920870
-
J. Yin, G. Chen, S. Yang, Z. Huang, and Y. Suo, “Ship autonomous berthing strategy based on improved linear-quadratic regulator,” Journal of Marine Science and Engineering, Vol. 12, No. 8, p. 1245, Jul. 2024, https://doi.org/10.3390/jmse12081245
-
R. Tchamna, M. Lee, I. Youn, V. Maxim, K. Židek, and T. Kelemenová, “Management of linear quadratic regulator optimal control with full-vehicle control case study,” International Journal of Advanced Robotic Systems, Vol. 13, No. 5, Sep. 2016, https://doi.org/10.1177/1729881416667610
-
Z. Bubnicki, Modern Control Theory. Berlin/Heidelberg: Springer-Verlag, 2005, https://doi.org/10.1007/3-540-28087-1
-
Y. K. Choi, M. J. Chung, and Z. Bien, “An adaptive control scheme for robot manipulators,” International Journal of Control, Vol. 44, No. 4, pp. 1185–1191, Oct. 1986, https://doi.org/10.1080/00207178608933659
-
I. Venanzi, “A review on adaptive methods for structural control,” The Open Civil Engineering Journal, Vol. 10, No. 1, pp. 653–667, Oct. 2016, https://doi.org/10.2174/1874149501610010653
-
W. Black, P. Haghi, and K. Ariyur, “Adaptive systems: history, techniques, problems, and perspectives,” Systems, Vol. 2, No. 4, pp. 606–660, Nov. 2014, https://doi.org/10.3390/systems2040606
-
M. Wang, “Adaptive control strategy for robot motion planning in complex environments,” Scientific Journal of Intelligent Systems Research, Vol. 6, No. 10, pp. 1–5, Nov. 2024, https://doi.org/10.54691/vmea5p42
-
J. Rakhmatillaev, V. Bucinskas, Z. Juraev, N. Kimsanboev, and U. Takabaev, “A recent lower limb exoskeleton robot for gait rehabilitation: a review,” Robotic Systems and Applications, Vol. 4, No. 2, pp. 68–87, Dec. 2024, https://doi.org/10.21595/rsa.2024.24662
-
D. Castellanos-Cárdenas et al., “A review on data-driven model-free sliding mode control,” Algorithms, Vol. 17, No. 12, p. 543, Dec. 2024, https://doi.org/10.3390/a17120543
-
V. Tinoco, M. F. Silva, F. N. Santos, R. Morais, S. A. Magalhães, and P. M. Oliveira, “A review of advanced controller methodologies for robotic manipulators,” International Journal of Dynamics and Control, Vol. 13, No. 1, Jan. 2025, https://doi.org/10.1007/s40435-024-01533-1
-
S. J. Gambhire, D. R. Kishore, P. S. Londhe, and S. N. Pawar, “Review of sliding mode based control techniques for control system applications,” International Journal of Dynamics and Control, Vol. 9, No. 1, pp. 363–378, May 2020, https://doi.org/10.1007/s40435-020-00638-7
-
A. T. Azar, F. E. Serrano, I. A. Hameed, N. A. Kamal, and S. Vaidyanathan, “Robust H-infinity decentralized control for industrial cooperative robots,” Advances in Intelligent Systems and Computing, pp. 254–265, Oct. 2019, https://doi.org/10.1007/978-3-030-31129-2_24
-
G. Rigatos and P. Siano, “An H-infinity feedback control approach to autonomous robot navigation,” in IECON 2014 – 40th Annual Conference of the IEEE Industrial Electronics Society, pp. 2689–2694, Oct. 2014, https://doi.org/10.1109/iecon.2014.7048886
-
H. El Hansali and M. Bennani, “H-infinity control of a six-legged robot in lifting mode,” International Review of Electrical Engineering (IREE), Vol. 16, No. 2, p. 174, Apr. 2021, https://doi.org/10.15866/iree.v16i2.18690
-
G. Rigatos, P. Siano, and G. Raffo, “An H-infinity nonlinear control approach for multi-DOF robotic manipulators,” IFAC-PapersOnLine, Vol. 49, No. 12, pp. 1406–1411, Jan. 2016, https://doi.org/10.1016/j.ifacol.2016.07.766
-
A. Rezaee, “Model predictive controller for mobile robot,” Transactions on Environment and Electrical Engineering, Vol. 2, No. 2, p. 18, Jun. 2017, https://doi.org/10.22149/teee.v2i2.96
-
Y. Ding, A. Pandala, and H.-W. Park, “Real-time model predictive control for versatile dynamic motions in quadrupedal robots,” in International Conference on Robotics and Automation (ICRA), pp. 8484–8490, May 2019, https://doi.org/10.1109/icra.2019.8793669
-
J. Cho and J. H. Park, “Model predictive control of running biped robot,” Applied Sciences, Vol. 12, No. 21, p. 11183, Nov. 2022, https://doi.org/10.3390/app122111183
-
T. Erez, K. Lowrey, Y. Tassa, V. Kumar, S. Kolev, and E. Todorov, “An integrated system for real-time model predictive control of humanoid robots,” in 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2013), pp. 292–299, Oct. 2013, https://doi.org/10.1109/humanoids.2013.7029990
-
Z. Zhang, X. Chang, H. Ma, H. An, and L. Lang, “Model predictive control of quadruped robot based on reinforcement learning,” Applied Sciences, Vol. 13, No. 1, p. 154, Dec. 2022, https://doi.org/10.3390/app13010154
-
I. Zaitceva and B. Andrievsky, “Methods of intelligent control in mechatronics and robotic engineering: a survey,” Electronics, Vol. 11, No. 15, p. 2443, Aug. 2022, https://doi.org/10.3390/electronics11152443
-
A. K. Abbas, Y. Al Mashhadany, M. J. Hameed, and S. Algburi, “Review of intelligent control systems with robotics,” Indonesian Journal of Electrical Engineering and Informatics (IJEEI), Vol. 10, No. 4, Nov. 2022, https://doi.org/10.52549/ijeei.v10i4.3628
-
L. Vladareanu, H. Yu, H. Wang, and Y. Feng, “Advanced intelligent control in robots,” Sensors, Vol. 23, No. 12, p. 5699, Jun. 2023, https://doi.org/10.3390/s23125699
-
V. Stoian and M. Ivanescu, “Robot control by fuzzy logic,” in Frontiers in Robotics, Automation and Control, InTech, 2008, https://doi.org/10.5772/6329
-
C.-H. Chen, C.-C. Wang, Y. T. Wang, and P. T. Wang, “Fuzzy logic controller design for intelligent robots,” Mathematical Problems in Engineering, Vol. 2017, No. 1, Sep. 2017, https://doi.org/10.1155/2017/8984713
-
A. Barzegar, F. Piltan, M. Vosoogh, A. M. Mirshekaran, and A. Siahbazi, “Design serial intelligent modified feedback linearization like controller with application to spherical motor,” International Journal of Information Technology and Computer Science, Vol. 6, No. 5, pp. 72–83, Apr. 2014, https://doi.org/10.5815/ijitcs.2014.05.10
-
Y. Jiang, C. Yang, J. Na, G. Li, Y. Li, and J. Zhong, “A brief review of neural networks based learning and control and their applications for robots,” Complexity, Vol. 2017, pp. 1–14, Jan. 2017, https://doi.org/10.1155/2017/1895897
-
A. Diouf, B. Belzile, M. Saad, and D. St-Onge, “Spherical rolling robots-Design, modeling, and control: A systematic literature review,” Robotics and Autonomous Systems, Vol. 175, p. 104657, May 2024, https://doi.org/10.1016/j.robot.2024.104657
-
J. Kober, J. A. Bagnell, and J. Peters, “Reinforcement learning in robotics: A survey,” The International Journal of Robotics Research, Vol. 32, No. 11, pp. 1238–1274, Aug. 2013, https://doi.org/10.1177/0278364913495721
-
V. A. Knights, O. Petrovska, and J. G. Kljusurić, “Nonlinear dynamics and machine learning for robotic control systems in IoT applications,” Future Internet, Vol. 16, No. 12, p. 435, Nov. 2024, https://doi.org/10.3390/fi16120435
-
S.-C. Chen, R. S. Pamungkas, and D. Schmidt, “The role of machine learning in improving robotic perception and decision making,” International Transactions on Artificial Intelligence (ITALIC), Vol. 3, No. 1, pp. 32–43, Nov. 2024, https://doi.org/10.33050/italic.v3i1.661
-
M. Wu, Y. Zhang, X. Wu, Z. Li, W. Chen, and L. Hao, “Review of modeling and control methods of soft robots based on machine learning,” in 42nd Chinese Control Conference (CCC), pp. 4318–4323, Jul. 2023, https://doi.org/10.23919/ccc58697.2023.10240787
-
A. Calzada-Garcia, J. G. Victores, F. J. Naranjo-Campos, and C. Balaguer, “A review on inverse kinematics, control and planning for robotic manipulators with and without obstacles via deep neural networks,” Algorithms, Vol. 18, No. 1, p. 23, Jan. 2025, https://doi.org/10.3390/a18010023
-
M. Soori, B. Arezoo, and R. Dastres, “Artificial intelligence, machine learning and deep learning in advanced robotics, a review,” Cognitive Robotics, Vol. 3, pp. 54–70, Jan. 2023, https://doi.org/10.1016/j.cogr.2023.04.001
-
M. Hongwei and F. Ghulam, “A review on linear and nonlinear control techniques for position and attitude control of a quadrotor,” Control and Intelligent Systems, Vol. 45, No. 1, Jan. 2017, https://doi.org/10.2316/journal.201.2017.1.201-2819
-
J. Iqbal, M. Ullah, S. G. Khan, B. Khelifa, and S. Ćuković, “Nonlinear control systems – a brief overview of historical and recent advances,” Nonlinear Engineering, Vol. 6, No. 4, Dec. 2017, https://doi.org/10.1515/nleng-2016-0077
-
S. Schaal and C. G. Atkeson, “Learning control in robotics,” IEEE Robotics and Automation Magazine, Vol. 17, No. 2, pp. 20–29, Jun. 2010, https://doi.org/10.1109/mra.2010.936957
-
C. Laschi, T. G. Thuruthel, F. Lida, R. Merzouki, and E. Falotico, “Learning-based control strategies for soft robots: theory, achievements, and future challenges,” IEEE Control Systems, Vol. 43, No. 3, pp. 100–113, Jun. 2023, https://doi.org/10.1109/mcs.2023.3253421
-
D. Valencia et al., “Comparison of model-based and model-free reinforcement learning for real-world dexterous robotic manipulation tasks,” in IEEE International Conference on Robotics and Automation (ICRA), pp. 871–878, May 2023, https://doi.org/10.1109/icra48891.2023.10160983
-
B. Zhang and P. Liu, “Model-based and model-free robot control: a review,” in Lecture Notes in Mechanical Engineering, Singapore: Springer Singapore, 2021, pp. 45–55, https://doi.org/10.1007/978-981-16-4803-8_6
-
H. R. Karimi, “How to deal with the complexity in robotic systems?,” Complex Engineering Systems, Vol. 2, No. 3, p. 15, Jan. 2022, https://doi.org/10.20517/ces.2022.33
-
S. J. Chacko, N. P. C., and R. J. Abraham, “Optimizing LQR controllers: a comparative study,” Results in Control and Optimization, Vol. 14, p. 100387, Mar. 2024, https://doi.org/10.1016/j.rico.2024.100387
-
T. Zhang, W. Zhang, and M. Gupta, “Resilient robots: concept, review, and future directions,” Robotics, Vol. 6, No. 4, p. 22, Sep. 2017, https://doi.org/10.3390/robotics6040022
-
J. Arents and M. Greitans, “Smart industrial robot control trends, challenges and opportunities within manufacturing,” Applied Sciences, Vol. 12, No. 2, p. 937, Jan. 2022, https://doi.org/10.3390/app12020937
-
C. Urrea and J. Kern, “Recent advances and challenges in industrial robotics: a systematic review of technological trends and emerging applications,” Processes, Vol. 13, No. 3, p. 832, Mar. 2025, https://doi.org/10.3390/pr13030832
-
T. Brogårdh, “Present and future robot control development-An industrial perspective,” Annual Reviews in Control, Vol. 31, No. 1, pp. 69–79, Jan. 2007, https://doi.org/10.1016/j.arcontrol.2007.01.002
-
D. Felix Brown and S. Quan Xie, “Effectiveness of intelligent control strategies in robot-assisted rehabilitation-a systematic review,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, Vol. 32, pp. 1828–1840, Jan. 2024, https://doi.org/10.1109/tnsre.2024.3396065
-
D.-A. Pham and S.-H. Han, “Design of combined neural network and fuzzy logic controller for marine rescue drone trajectory-tracking,” Journal of Marine Science and Engineering, Vol. 10, No. 11, p. 1716, Nov. 2022, https://doi.org/10.3390/jmse10111716
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
