Bearing fault diagnosis based on multi-scale spectral images and convolutional neural network

2.1. Overview of FFT algorithm

The Fourier transform is one of the fundamental methods for transforming time-domain series to frequency-domain. The frequency spectrum information of the signal at discrete frequency points can be obtained through discrete Fourier transform (DFT) processing. For a discrete-time signal $x\left[n\right](n=\mathrm{0,1},\cdots ,N-1)$, its DFT is defined as follows:

where $k=\mathrm{0,1},\cdots ,N-1$.

Fast Fourier transform (FFT) is an efficient algorithm for computing the DFT. When the number of data points is $N=2^m$ (where $m$ is a positive integer), it can reduce computing complexity dramatically for analyzing data using FFT. To lay the foundation for constructing MSSI features in subsequent stages, FFT is applied for generating spectrum with different frequency resolutions, which is achieved by taking different values of $m$ in $N=2^m$ in this study.

2.2. Construction of the MSSI feature

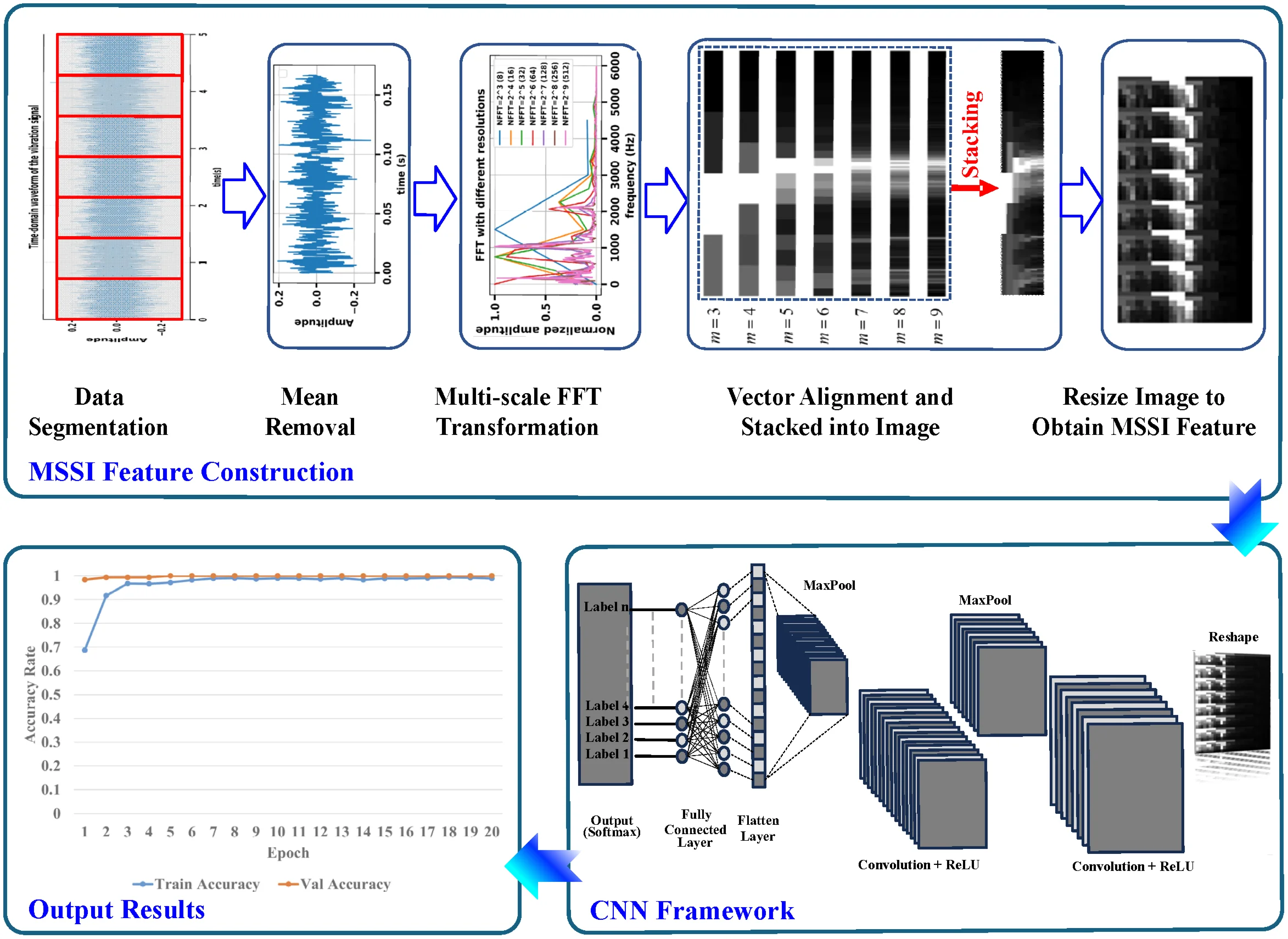
The frequency spectrum contains a large amount of characteristic information about the running process of a bearing, such as the fault characteristic frequencies and their harmonics, the geometrical structure of the spectrum, and so on. Aiming at mining the health information contained in the spectrum as much as possible, a novel feature named MSSI is innovatively constructed by generating a series of spectrum using different frequency resolutions. The construction process of the proposed MSSI feature is presented in Fig. 1.

First, the collected original vibration data are first divided into sub-signals and then the signals are detrended through mean removal processing.

Second, multi-scale FFT transformation is performed to obtain the spectrum with FFT using different frequency resolutions, which achieved by setting the variable $m$ in section 2.1 as different positive integers. And the variable $m$ is set 3 to 9 in this paper. In addition, all spectrum sequences are pre-processed using the maximum-minimum normalization method to eliminate the effects of different magnitudes for MSSI construction.

Fig. 1Construction process of the proposed MSSI feature

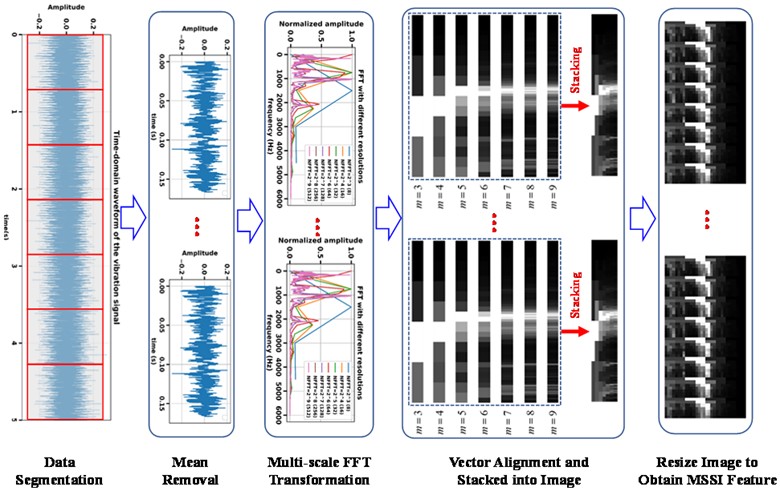
Third, since the length of spectrum sequences vary with frequency resolutions, the vector alignment processing is performed on the aforementioned sequence. All spectrum sequences will be of the same length to facilitate subsequent construction of MSSI feature. In this study, the elements in shorter vectors are uniformly replicated to extend their lengths to match the reference sequence namely the longest one, through proportional element duplication. Then these aligned sequences are stacked into an image in order. An example of the vector alignment processing and vector stacking is presented in Fig. 2. Suppose that there are four series generated with $m=$4-7, the first three sequences are aligned to the last one that served as the reference during the alignment process. Subsequently, these aligned sequences are ordered into a matrix to obtain the image feature.

Finally, the above-mentioned image feature is usually an elongated image, which is not conducive to the further processing for the image features and the final fault diagnosis. Therefore, the image features obtained in the previous step are resized to an approximately square image (with size 56×32 in pixels in this study), which is called as the MSSI feature.

3.1. CNN model design

This network framework is inspired by the typical LeNet-5 [14] and the proposed CNN architecture is based on the same strategy, using convolutional and pooling layers to extract image features and fully connected layers for classification.

Fig. 3The proposed CNN framework

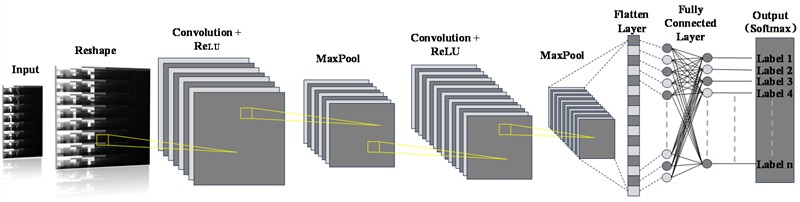
Compared to the original LeNet-5, this network makes a series of changes in detail, including different number of convolutional kernels and layers, and introduces a dropout layer to mitigate the risk of overfitting [15]. To facilitate feature extraction and classification using CNN model, an input image of size 56×32 (in pixels) is first reshaped to a 128×128 (in pixels) image by nearest neighbor interpolation. The proposed CNN framework is presented in Fig. 3.

The parameters of the proposed CNN architecture are shown in Table 1. In this research, we design two convolutional layers. The kernel size for both layers is 3×3, and the stride is set to 1 by default. The first convolutional layer (Conv1) uses 16 kernels, while the second convolutional layer (Conv2) contains 32 kernels, which enhances the model's feature learning capacity. Zero padding is applied to ensure that the input and output sizes remain unchanged, which adds zeros around the borders of the input volume. It is used to maintain the same spatial dimensions between the input and output volumes, thereby preserving as much information as possible from the original input [14]. The calculation formula of the convolutional layer is as follows:

where $X(i,j)$ represents the value of the input feature at position $(i,j)$, $W(m,n)$ represents the weight of the convolution kernel at $(m,n)$ and $b$ represents the bias, $Y(i,j)$ represents the value of the output feature map at position $(i,j)$. $M\times N$ is the size of the convolution kernel and $S$ represents the stride. In convolutional layer, $S$ is set to 1 by default and $M\times N$ is set to 3×3. $P$ represents the padding and the calculation formula of the output feature map as follows:

where $H_{in}$ and $W_{in}$ represents the height and width of the input feature map, which is 128×128, $H_{out}$ and $W_{out}$ represents the height and width of the output feature map, which is 128×128, according to the formula we can get $P$ equals 1.

Additionally, two Max Pooling layers are incorporated, with a kernel size of 2×2 and a stride of 2. This pooling operation preserves the most significant features in the input feature map, while reducing its size, thereby decreasing the computational burden of subsequent layers. The expression of the maximum pooling layer in the pooling layer is as follows:

where $S$ represents the stride in the pooling layer, which is set to 2, $m$ and $n$ are the length and width of the pooling kernel, which is 2×2.

After the input image passes through the convolution layer and the pooling layer, it needs to rely on the fully connected layer to classify the extracted features. In the fully connected layer, all input feature maps are expanded into one-dimensional feature vectors, weighted summed and activated by the activation function. We add two fully connected layers, FC1 and FC2, are designed, with FC1 consisting of 256 neurons and FC2 containing 10 neurons. Since FC2 serves as both the fully connected layer and the output layer, it is designed with 10 neurons to match the number of output classes. The fully connected layer can be expressed as follows [16]:

where $Y$ represents the output of the neuron and $\phi \left(x\right)$ represents the activation function and $k-1$ represents the $\left(k-1\right)$th fully connected layer and $w^{k-1}$ represents the weight matrix connecting the $\left(k-1\right)$th layer to the $k^{th}$ layer and $x^{k-1}$ represents the output vector from the $\left(k-1\right)$th layer and $b$ represents the bias.

The cross-entropy loss function is applied in our research, which includes the softmax function, so the softmax is not explicitly applied in the model, and an L2 regularization parameter of 0.0001 is applied, to enhance the model performance and generalization. The cross-entropy loss function can be represented as follows [17]:

where $n$ represents the number of classes and $l_i$ represents truth label and $y_i$ represents the probability predicted by the model and $W$ represents the weight parameter matrix of the neural network and ${‖W‖}_2^{}$ represents the L2 norm of the weight and $\lambda$ represents the weight decay, which is set to 0.0001.

A dropout layer with a dropout rate of 0.5 is introduced to prevent overfitting. The Adam optimizer is employed with a learning rate of 0.001. The hyperparameter information of the proposed CNN structure is summarized in Table 2.

3.2. The proposed fault diagnosis scheme

The diagnosis model is first established using the MSSI features derived from the offline vibration data and deep learning technology in the offline training procedure. Then the bearing health states can be diagnosed with the trained model by inputting the MSSI features derived from the online monitoring data. The main process can be summarized as follows.

(1) MSSI Feature Extraction: The MSSI features of the offline or the online vibration signals are constructed using the method in Section 2.

(2) CNN Model Building: The CNN parameters are initialized at first, and the MSSI features of the offline data are input to the CNN. Then the forward propagation algorithm is used to calculate the training error and the back propagation algorithm to obtain the error and gradients. Finally, the parameters are adjusted according to the obtained error and gradients to optimize the CNN model, thereafter a trained CNN model is obtained and can be applied for final fault diagnosis.

(3) Online Fault Diagnosis: The MSSI feature of an online data sample is input to trained CNN model to diagnose the corresponding health state of bearing.

The overall flowchart of the proposed fault diagnosis scheme is shown in Fig. 4.

4.1. Case analysis on CWRU data

4.1.1. Introduction to CWRU bearing data

This validation data comes from the publicly available rolling bearing dataset from Case Western Reserve University (CWRU) [18]. As shown in Fig. 5, the test rig consists of a 2 hp motor (left), a torque transducer/encoder (center), a dynamometer (right), and control electronics (not shown). The testing bearing were installed on the motor housing at the drive end of the motor and the bearing outer ring was attached with the motor housing. The vibration signals were acquired using acceleration transducer. Four bearing health state (normal, inner race fault, rolling element fault, and outer race fault) and four levels of fault severity (7 mils, 14 mils, 21 mils and 28 mils) are considered in the experiment. And the vibration data under four different load/speed conditions (Load0 = 0 hp/1797 rpm, Load1 = 1 hp/1772 rpm, Load2 = 2 hp/1750 rpm and Load3 = 3 hp/1730 rpm) were sampled using the accelerometers attached to the drive end of the motor housing with 12 kHz sampling rate.

Fig. 4Flow chart of fault diagnosis based on MSSI and CNN

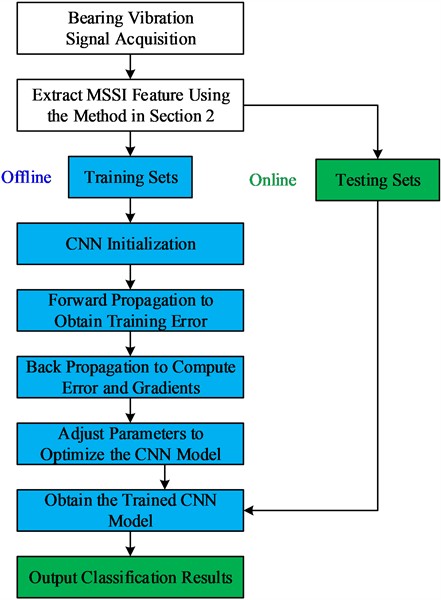
Fig. 5The test rig for CWRU bearing data [18]

In order to facilitate the MSSI for extracting more fault information and enrich the data set, a data division strategy is employed for data segmentation shown in Fig. 1, in which a length of about 1/6 second data is applied for data segmentation. In other words, it can be guaranteed that a single sample could contain vibration data of five shaft rotations. This temporal span guarantees the comprehensive acquisition of bearing signals.

4.1.2. Results analysis

A comprehensive ten class diagnosis problem is employed to evaluate the performance of the proposed method. This instance involves fault type diagnosis and fault severity diagnosis, which makes it the most challenging diagnostic problem using the CWRU data. Here several diagnosis cases under single running condition and multiple running conditions are employed for validation analysis. As shown in Table 3, vibration datasets under four running conditions (Load0, Load1, Load2 and Load3) are represented by A, B, C and D, respectively. And the vibration datasets under Load0-Load3 conditions is designated as E. The sample number under different running conditions is different due to the different lengths of the original data. The sample number of the normal state under Load0 is 120, while the sample number of the normal state under Load1, Load2 or Load3 is 240. The sample number of other health states is 60 or 61. Meanwhile, 70 % of the total samples is randomly selected as the training set for constructing CNN model and the remaining 30 % as the testing set for examining model classification ability.

Table 3Description of the CWRU bearing datasets

Health state			Normal	Inner race fault			Ball fault			Outer race fault
Fault diameter (mil)			0	7	14	21	7	14	21	7	14	21
Classification label			NM	IR1	IR2	IR3	B1	B2	B3	OR1	OR2	OR3
Dataset A	Load0	Train	84	42	42	43	43	42	42	42	42	43
		Test	36	18	18	18	18	18	18	18	18	18
Dataset B	Load1	Train	168	42	42	42	42	43	42	43	43	42
		Test	72	18	18	18	18	18	18	18	18	18
Dataset C	Load2	Train	168	43	42	42	42	42	43	42	42	43
		Test	72	18	18	18	18	18	18	18	18	18
Dataset D	Load3	Train	168	43	42	42	42	43	43	43	42	42
		Test	72	18	18	18	18	18	18	18	18	18
Dataset E	Load0-Load3	Train	588	170	168	169	169	170	170	170	169	170
		Test	252	72	72	72	72	72	72	72	72	72

The MSSI features were first extracted from both the training set and the testing set using the method presented in section 2. In order to present the proposed MSSI features intuitively, an example of MSSI feature for the ten health states under Load0 condition is given in Fig. 6. The MSSI features of ten health conditions are visualized after reshaping the original 7×256 spectral representations into 56×32 grayscale images. As presented in Fig. 6, the row axis corresponds to frequency components ranging from low to high, while the column axis denote spectral energy distribution under different frequency resolution in a specific frequency band, where each group of rows (8-pixel height) reflects the spectral response under a specific FFT length (from 2³ to 2⁹).

To quantitatively characterize these differences, mean gray value (representing the average pixel intensity of the image), standard deviation (quantifying the dispersion of pixel intensities and thus reflecting image contrast and detail), and information entropy (measuring the randomness or information content of the pixel intensity distribution), were employed for further quantitative analysis. In particular, the information entropy is a classic statistic that measures the uncertainty of grayscale distribution in an image and is widely used to describe the complexity and information richness of an image. For the normalized images in the range $\left[\mathrm{0,1}\right]$ in this study, it is necessary to discretize the normalized values into a finite set of gray levels prior to entropy computation. This is typically achieved by mapping each normalized pixel value $x_i\in [0,1]$ to an integer grayscale level $k_i\in \{\mathrm{0,1},\cdots ,255\}$ by $k_i=\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}(255\times x_i)$. Then the information entropy can be calculated as follows:

8

$H=-{\sum }_{k=0}^{255}p\left(k\right){\log }_{2}p\left(k\right),$

where $H$ represents the information entropy of the image and $p\left(k\right)$ represents the appearing probability of gray level 𝑘, which is calculated as the number of pixels with gray value 𝑘 divided by the total number of pixels in the image.

Table 4 summarizes three statistical metric values under different health conditions shown in Fig. 6. These metrics provide objective evidence supporting the qualitative observations and further distinguish the fault types based on their spectral image characteristics. Also, it can be seen that there are relatively obvious differences between the MSSI features for different health states.

Fig. 6An example of MSSI feature for the ten health states under Load0 condition

a) B1

b) B2

c) B3

d) IR1

e) IR2

f) NM

g) OR1

h) OR2

i) OR3

j) IR3

Table 4Three statistical metrics under different health conditions

Metrics	NM	B1	B2	B3	IR1	IR2	IR3	OR1	OR2	OR3
Mean gray value	0.151	0.206	0.247	0.222	0.313	0.307	0.199	0.192	0.249	0.268
Standard deviation	0.272	0.275	0.287	0.27	0.309	0.313	0.288	0.294	0.27	0.305
Information entropy	4.76	5.73	5.91	5.86	6.18	6.22	5.62	5.39	6.80	6.01

After all MSSI features were extracted, the randomly selected training samples under different load/speed conditions were applied to train the CNN model. An example of the training process of CNN model for Dataset E is given in Fig. 7. It can be seen that the loss rate drops rapidly and remains in a very small range, and both the train and validation accuracies are approximate to 100.00 % after about the 7th epoch.

Fig. 7An example of the training process of CNN model for Dataset E

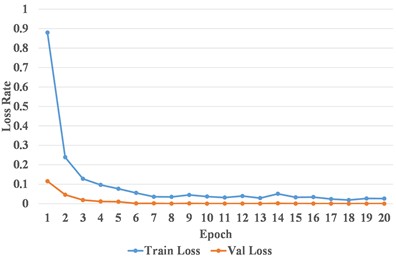
a) Loss curve

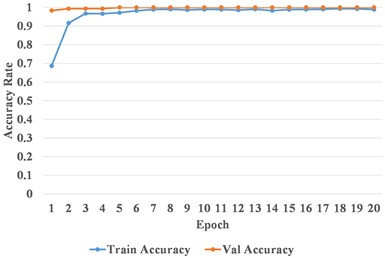
b) Accuracy curve

Then the remaining testing samples were input to the trained CNN model to validate the effectiveness of the proposed fault diagnosis scheme. Ten trials were conducted to record the classification results and compute the average diagnostic accuracy. The accuracy results of the CWRU bearing set are presented in Table 5 and Table 6. In the context of diagnostic case analysis under single running conditions, the testing samples from Dataset A, B, C and D were classified with average accuracy of 99.80 %, 99.87 %, 100.00 % and 99.96 %, respectively. For the diagnostic cases under multiple running conditions, the proposed framework exhibits robust performance with 99.99 % classification accuracy for Dataset E. Examining the results, it can be observed that most testing samples are classified correctly and the proposed method demonstrates consistently high accuracy across all running conditions.

Table 5Experimental results for single running condition

Dataset	Average accuracy	Standard deviation
A	99.80 %	0.350 %
B	99.87 %	0.400 %
C	100.00 %	0.000 %
D	99.96 %	0.140 %

Table 6Experimental results for multiple running conditions

Dataset	Testing accuracy				Total accuracy	Standard deviation
	Load0	Load1	Load2	Load3
E	99.95 %	100.00 %	100.00 %	100.00 %	99.99 %	0.026 %

As shown in Table 5 and Table 6, it can also be shown that the results demonstrate inferior performance on Dataset A and Dataset B. The confusion matrices of the CNN models for Dataset A and Dataset B are presented in Fig. 8. It can be observed that the models are generally effective in distinguishing between different fault types. However, there exists a potential misclassification of B2 as B1 in Dataset A; similarly, B3 in Dataset B may have been erroneously classified as B1. The main reason could be that the impact energy generated by the defects of the rolling elements is weak and significantly lower than that of the other faults (e.g. the inner race or outer race faults) especially under light-load conditions, which results in a relatively poor discrimination in the spectrums and the MSSI features.

Fig. 8The confusion matrices of CNN model for Dataset A and Dataset B

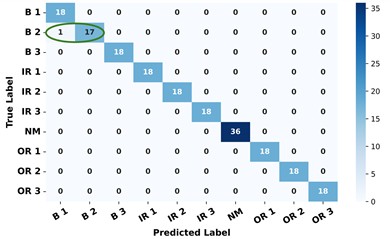
a) Confusion matrix for Dataset A

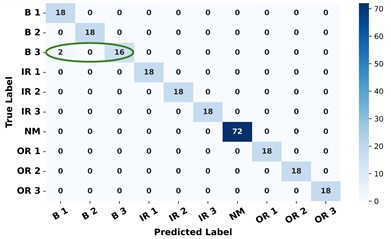
b) Confusion matrix for Dataset B

4.2. Case analysis on a conveyor idler dataset

4.2.1. Introduction to the conveyor idler testbed

The test bench shown in Fig. 9 consists of an AC motor, a frequency converter, a conveyor idler, a tachometer, an accelerometer, a signal acquisition instrument and a computer [19]. A normal bearing (6204 type) is installed on one end and the test bearing is installed on the other end (the right end shown in Fig. 9) of the conveyor idler, which is driven by a belt through the AC motor. The bearing inner ring was attached with the idler shaft. The type of both normal and tested bearings is 6204. Five bearing health states (normal, inner race fault, rolling element fault, outer race fault and cage fault) are considered in the experiment, and the vibration signals at a motor speed of 1080 rpm were collected using the sensors and the signal acquisition instrument with 20 kHz sampling frequency. One million data points (i.e., 50 s) were recorded in a sampling signal and the signals were sampled twice for different bearing health states of the conveyor idler. More details about the experimental platform can refer to [19].

Fig. 9Test bench of the belt conveyor idler [19]

4.2.2. Results analysis

Similarly, to enhance the capability of MSSI in extracting fault-related information, a data division strategy is implemented for segmentation, as illustrated in Fig. 1. Each sample is ensured to contain vibration data corresponding to about seven shaft rotations, where this duration is sufficient to ensure the comprehensive acquisition of conveyor idler signals. Therefore, a total of 298 samples are obtained for each of the five health states. Similarly, 70 % of the total samples is randomly selected to train the CNN model and the remaining 30 % is applied for testing the model diagnostic ability. The sizes of datasets for different health states are presented in Table 7.

An example of MSSI features for the conveyor idler bearing under different health states is presented in Fig. 10. It is evident that the characteristic differences can still be depicted between the MSSI features for different fault types. The MSSI features derived from training set were used to train the CNN model. Also, an example of the CNN training process is presented in Fig. 11. It can be observed that the loss rate decreases rapidly and stabilizes within a narrow range, while both the training and validation accuracies approach 100.00 % after approximately the 8th epoch.

Table 7Description of the conveyor idler bearing datasets

Label	Health state	Training set	Testing set
IR	Inner race fault	209	89
B	Rolling element fault	209	89
OR	Outer race fault	209	89
NM	Normal	209	89
CA	Cage fault	209	89
Total	/	1045	445

Table 8Accuracy results of the conveyor idler bearing analysis

Label	IR	B	OR	NM	CA	Average accuracy	Standard deviation
Accuracy	100.00 %	100.00 %	100.00 %	100.00 %	100.00 %	100.00 %	0.000 %

Once the CNN model is built, the testing samples were input to validate the performance of the proposed method. Then ten trials were conducted to obtain average results, ensuring the outcomes are generalizable and not influenced by special cases. The accuracy results are shown in Table 8. It can be seen that all the testing samples were classified with 100 % accuracy. This further substantiates the reliability and validity of the methodology proposed in this paper.

Fig. 10An example of MSSI features for the conveyor idler bearing under different health states

a) NM

b) IR

c) OR

d) B

e) CA

Fig. 11An example of the training process of CNN model for conveyor idler bearing

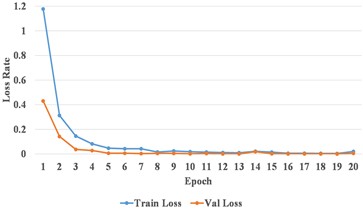
a) Loss curve

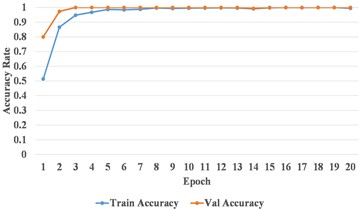
b) Accuracy curve

4.3. Discussion

According to the experimental results, the proposed method demonstrates high diagnostic accuracy on both the CWRU dataset and the conveyor idler dataset. However, for the CWRU dataset, the classification accuracies under Load0 and Load1 conditions are relatively lower. As indicated by the corresponding confusion matrices, there is a tendency for misclassification between B1 and B2 under Load0, and between B1 and B3 under Load1. This is primarily attributed to the high similarity in fault features among rolling element defects of different sizes within the same fault type. Such similarity poses challenges for accurate discrimination using the proposed method to diagnose different fault severities.

In order to further compare the reliability and the potential application of the proposed scheme, a comparative study between current work and some published works is presented in Table 9. These published methods are all verified and the ten classifications problem under single and/or multiple operational scenarios are considered with the same CWRU bearing data. As presented in Table 9, bearing faults were diagnosed with GAF-CA-CNN model using GAF image as feature in [20]. In [17], time-frequency images were extracted and applied for fault diagnosis, and bearing faults were diagnosed with CNN, ResNet-18 or RNELM models. In [21], ensemble deep neural network and CNN is proposed as model for bearing fault diagnosis using vibration signal and statistical feature. A detailed result comparison between this work and those published works is presented in Table 9. It can be seen that the proposed scheme shows better performance for bearing fault diagnosis than the others. Furthermore, only using a lightweight CNN, the proposed MSSI feature is evidently superior to other features, even to the time-frequency image combined with some advanced models, such as ResNet-18 or RNELM presented in [17]. This indicates that the proposed MSSI feature is a more promising and effective 2-D feature for bearing fault diagnosis.

Otherwise, the time costs of MSSI feature construction, model training, and model diagnosis were calculated to evaluate the feasibility of industrial implementation of the proposed method. All tests were conducted using MATLAB R2024b and PyCharm Community Edition 2023.1.3. Specifically, MATLAB was employed for preprocessing the time-series vibration signals and generating MSSI features. Subsequently, the extracted feature were utilized for model training and fault diagnosis with PyCharm, leveraging the PyTorch framework (version 2.4.1 + cu124). The detailed hardware and software configurations are summarized in Table 10.

Here, the time cost evaluations were conducted using CWRU data from Load0 condition as an example to evaluate the time consumption at different stages of the process. The results are presented in Table 11.

According to Table 11, the average time required for the MSSI feature construction is approximately 0.1831 seconds per sample. The model training phase has a total duration of 5.273 seconds for 20 epochs, and the average training time per epoch is approximately 0.2637 seconds. In the diagnosis stage, the model demonstrates high computational efficiency, with an average inference time of only 0.0014 seconds per testing sample. The experimental results demonstrate that both the MSSI construction process and CNN-based diagnosis exhibit significantly low computational time consumption, which substantiates the industrial applicability of the proposed methodology.