Abstract
The accurate estimation of vehicle state parameters has a significant impact on the active safety system of automobiles. Accurately obtaining vehicle operating parameters is the foundation and prerequisite for active safety control of vehicles. In response to the limited estimation accuracy of the traditional CKF method, the CKF was extended to fifth-order according to the third-order sphere-radius cubature rule, making it have the accuracy of fifth-order Taylor series expansion. At the same time, singular value decomposition was used instead of traditional Cholesky decomposition to form a fifth-order cubature Kalman filter (SVD-FCKF) estimator for singular value decomposition. Then, the SVD-FCKF was validated using the Carsim and Matlab/Simulink joint simulation platform. Finally, the effectiveness of the proposed method was verified through virtual experiments. The results show that the improved SVD-FCKF estimator can effectively improve the accuracy and stability of vehicle state estimation, with overall estimation performance better than the CKF estimator and has strong adaptability under high and low adhesion coefficient conditions. The research results can provide theoretical support for the active safety research of intelligent vehicles and have practical application value.
Highlights
- The improved SVD-FCKF estimator can effectively improve the accuracy and stability of vehicle state estimation, with overall estimation performance better than the CKF estimator and has strong adaptability under high and low adhesion coefficient conditions.
- The research results can provide theoretical support for the active safety research of intelligent vehicles and have practical application value.
1. Introduction
Today, with the increasing number of vehicles on the road and the increasingly complex traffic environment, driving safety is facing severe challenges. Intelligent vehicles equipped with advanced driving assistance systems have become a research hotspot due to their ability of reducing the driver operation load and assisting the driver in achieving safe driving. Accurately and real-time obtaining vehicle driving status information is the key to achieve effective decision-making and control of intelligent vehicles. The active safety technology of automobiles has always been a focus of attention. Active safety can help improve the maneuverability and stability of vehicles, thereby reducing the probability of accidents. One of the key aspects of active safety technology is to accurately obtain the real-time status of the vehicle, including its yaw rate, longitudinal and lateral velocity, and side slip angle. There are two main ways to obtain vehicle status parameters. One is based on sensor measurement, but due to the high cost of sensors, algorithms are currently more commonly used for estimation. The acquisition of vehicle driving state parameters is the basis for the active safety of vehicles, but due to the cost of sensors or the inability to directly measure parameters, accurate estimation of vehicle driving state parameters by low-cost estimators is crucial [1-3].
The idea of Cubature Kalman Filter was originally presented by Ienkaran Arasaratnam and Simon Haykin [4]. Over the past few decades, intelligent connected vehicles have received increasing attention for their large benefits in improving road safety [5-8]. Compared with EKF, the UKF can be applied to nonlinear distributed systems, achieving higher computational accuracy [9-14]. Most estimation algorithms based on KF had higher estimation accuracy, but they were limited by the vehicle kinematic model and required accurate model parameters, so KF based algorithms had certain limitations [15-17]. In order to solve the problem of relying on kinematic models, some studies had applied machine learning algorithms to vehicle state estimation. Machine learning based regression algorithms did not rely on automotive kinematic models and inherent vehicle parameters, but estimated vehicle state parameters through model structure and training datasets [18]. At the same time the neural network and the sensor fusion technologies are used for the vehicle state estimation [19-21]. Cubature-Kalman filter is widely used for nonlinear dynamic estimations due to its high accuracy and numerical stability [22-26].
In recent years, scholars have found that CKF has strong adaptability, but its estimation accuracy is low or even divergent in strongly nonlinear system environments such as distributed drive electric vehicles. Zhao et al. estimated the yaw rate, longitudinal speed, and side slip angle based on the 3-DOF dynamic model based on the front wheel angle and longitudinal acceleration. By comparing the UKF and EKF algorithms, the efficiency and accuracy of the application of the UKF in the estimation of vehicle handling stability states and parameters were verified. The method described in the article controlled the driving or braking torque of the vehicle, effectively improving the slipping and locking conditions during driving and braking, ensuring the safety of the vehicle operation [27]. Lu et al. designed a nonlinear full dimensional observer and a UKF observer based on vehicle sensors, and compared and analyzed the two estimation methods under extreme conditions. The prediction performance of the nonlinear full dimensional observer was slightly higher under extreme conditions [28]. Pan et al. studied the lateral stability of vehicles based on the Uni-tire model and 2-DOF dynamic model, and designed a side slip angle estimator, which significantly improved the estimation effect and provided more accurate prediction values for the design of vehicle control strategies [29]. Particle Filter is widely used for nonlinear dynamic estimations especially in the field of vehicle state estimation [30-32].
The Kalman filter estimation algorithms studied above are all based on the improvement of third-order accuracy, which limits the improvement of their accuracy. Other estimation algorithms mainly fuse different algorithms, which are computationally complex and have high levels of algorithm constraints. They do not have high estimation accuracy for high-dimensional nonlinear models. In response to the limitations of traditional third-order CKF, this paper extends it using the fifth-order sphere-radius cubature rule to form a fifth-order CKF. At the same time, in the filtering process of the fifth-order CKF, a more stable singular value decomposition is used instead of Cholesky decomposition, further improving the estimation accuracy of the algorithm. During the CKF iteration process, it is necessary to generate cubature points. The generation of cubature points is related to the error covariance matrix. Generally, in the calculation process, the error covariance matrix needs to be subjected to Cholesky decomposition to obtain the volume points, which requires the error covariance matrix to maintain positive definiteness at all times. Errors may occur during the computer process, causing the covariance matrix to become non positive definite during the update process, resulting in the inability to perform Cholesky decomposition properly and causing the algorithm to fail in computation.
2. Mathematical model of vehicle state estimation problem
2.1. 3-DOF vehicle model
The vehicle state estimation model is established based on a 3-DOF vehicle model:
The dynamic equation of the 3-DOF vehicle model is as follows [33]:
The side slip angle of the center of mass is:
Fig. 13-DOF vehicle model
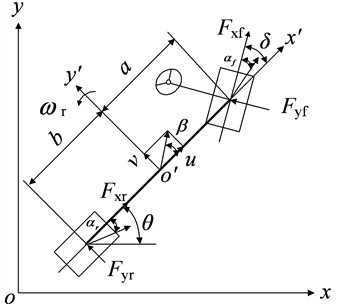
2.2. Tire model
The lateral forces of front and rear wheels can be expressed as:
where and are the lateral stiffness of the front and rear tires. and are the front and rear slip angles:
3. SVD FCKF estimator
For the following discrete-time nonlinear dynamic systems:
where and are the state and observation vectors of the system at time k; and are the system state transition function and the observation function; and are the process noise and observation noise which are uncorrelated and follow a normal distribution, and ; is the covariance matrix of the process noise; is the mean square error matrix of the observation noise.
3.1. Fifth-order sphere-radius cubature rule
When considering nonlinear dynamical systems under Gaussian assumptions, approximate values of multidimensional Gaussian weighted function integrals are calculated using the sphere-radius cubature rule. For different cubature points and weights, they should be determined by cubature rules of different orders. And the results obtained based on Gaussian-Laguerre integration will not be the same. For third-order CKF, if all third-order polynomials in -dimensional vector space can be obtained according to the sphere-radius cubature rule, then the third-order sphere-radius cubature rule can be represented by extending the Gaussian-Laguerre integral. At present, the cubature rule can accurately represent monomials of third-order and below. The fifth-order sphere-radius cubature rule can be obtained as [34]:
where ; ; is the unit vector in an -dimensional vector space, with the th element being 1 and all other elements being 0.
By combining Gaussian weighting function integration, spherical cubature rule, and the expression of integration points and their prerequisites, the fifth order spherical-radial cubature rule using cubature points can be obtained:
where ; .
3.2. SVD-FCKF algorithm
The FCKF algorithm based on high-order sphere-radius cubature rule has higher computational efficiency compared to third-order CKF and has been widely used in GPS/INS navigation systems. By replacing the Cholesky decomposition in the traditional CKF algorithm with more numerically stable singular value decomposition, the resulting covariance matrix is used as the characteristic covariance matrix. Thus, the SVD-FCKF algorithm for vehicle state estimation is constructed, and its specific calculation process is as follows.
3.2.1. Time updating
To calculate the cubature points at time , the covariance matrix is decomposed using SVD:
The column vectors of and are the left and right singular value vectors of respectively; ; is the dimension of the state vector. is expressed as:
where ; the element of the -dimensional unit vector is 0 except for the th element which is 1. and are expressed as:
The transferring cubature point of nonlinear state equation is calculated:
The prediction value of the state at time is calculated:
where the weight is expressed as:
The covariance matrix of state error at time is calculated:
where is the system noise covariance.
3.3. Measurement updating
The cubature points after measurement updating is calculated by decomposing the covariance matrix at time using SVD:
The cubature point transmitted through the measurement equation is calculated:
The SVD-FCKF gain matrix is calculated:
The state estimation value and state error covariance matrix at time is calculated:
In this algorithm, the information from the observed residual sequence is applied to adaptively update the noise covariance matrix, instead of using a fixed noise covariance matrix for recursive estimation to improve the estimation accuracy of the algorithm. The specific calculation method is as follows.
The residual of the relevant output observation vector is calculated as:
The residual covariance matrix of the relevant output observation vector is calculated as:
The covariance matrix of the process noise at time is updated as follows:
The covariance matrix of the observation noise at time is updated as follows:
4. Numerical simulation and experimental verification
This article uses the SVD-FCKF method to filter and estimate the yaw rate and side slip angle as well as longitudinal velocity. A Carsim and Matlab/Simulink joint simulation platform is established for simulation and the results are compared and analyzed with the CKF method.
4.1. Numerical simulation
4.1.1. = 0.85
In the simulation sampling period is set as 0.001 s; the covariance matrix of the system noise is and the initial value of the covariance matrix of the measurement noise is .
The simulation results of the yaw rate and side slip angle as well as longitudinal velocity of the vehicle under the condition of = 0.85 are shown in Fig. 2.
From Fig. 2, it can be seen that the curve obtained by the SVD-FCKF estimator is more in line with the reference values than the curve obtained by the CKF estimator. And the effect is more significant at the peak and valley of the curve. The reason for this trend is that the steering angle at the peak and valley changes at high speed causing significant fluctuations in the vehicle state. At this time, the CKF processing highly nonlinear systems in the third-order dimension can easily accumulate errors, resulting in estimation results deviating from actual values. However, the SVD-FCKF can control the accumulation of errors and obtain more accurate estimation results through a fifth-order Taylor expansion. The SVD-FCKF estimator and CKF estimator maintained a good fit with the reference value in the first 1 second. But after 1 second, the estimated value of the CKF gradually deviated from the reference value, while the SVD-FCKF still maintained good estimation performance. This is because singular value decomposition can reduce the influence of noise in the estimation process and improve the robustness of the system and reduce the influence of state estimation errors and ensure that the estimation results always converge to the reference value. At the same time, singular value decomposition and Cholesky decomposition are two different matrix decomposition methods that are applicable to different types of matrices. Singular value decomposition has the following advantages over Cholesky decomposition: Cholesky decomposition is mainly used for decomposing symmetric positive definite matrices, while singular value decomposition can be used for decomposing any matrix, making the application scenarios of singular value decomposition more extensive.
In order to further compare the estimation accuracy of the algorithm, the root mean square error (RMSE) is used to evaluate and compare the estimation accuracy, as shown in Table 1. From Table 1, it can be seen that the RMSE of the yaw rate and side slip angle as well as the longitudinal velocity calculated by the SVD-FCKF algorithm is smaller than that of the CKF algorithm.
Fig. 2Simulation results under the condition of μ= 0.85: a) yaw rate; b) error of yaw rate; c) side slip angle; d) error of side slip angle; e) longitudinal velocity; f) error of longitudinal velocity
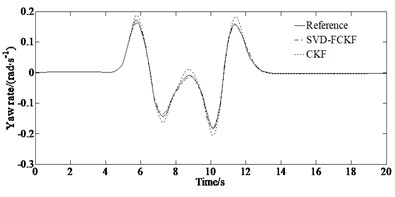
a)
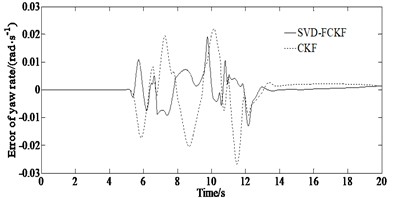
b)
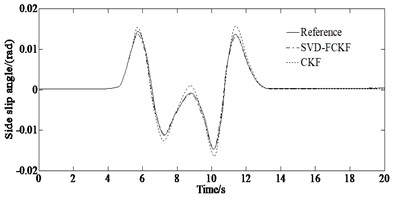
c)
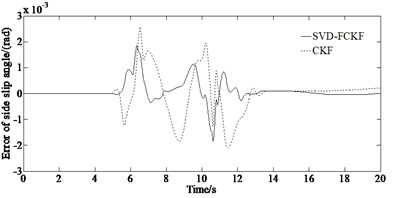
d)
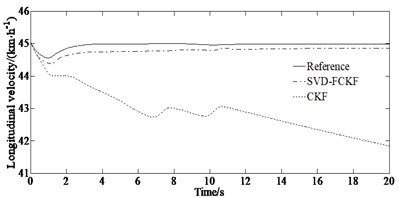
e)
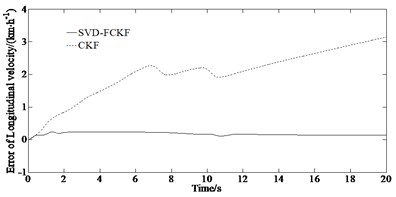
f)
Table 1The RMSE indicators of the two algorithms
Evaluation index | State value | SVD-FCKF | CKF |
RMSE | (rad/s) | 0.00279 | 0.00566 |
(rad) | 0.000441 | 0.000672 | |
(km/h) | 0.1629 | 1.1432 |
4.1.2. =0.2
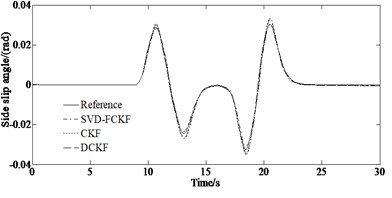
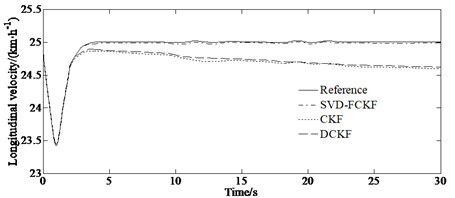
The simulation results of the yaw rate and side slip angle as well as longitudinal velocity of the vehicle under condition of = 0.2 are shown in Fig. 3.
From Figs. 3 (a)-(b), it can be seen that the longitudinal velocity estimated by SVD-FCKF and CKF estimators are generally consistent with the reference values. However, the overall error of the SVD-FCKF is smaller than that of the CKF, indicating higher estimation accuracy. From Fig. 3(c), it can be seen that the longitudinal velocity errors estimated by the SVD-FCKF estimator under low adhesion coefficient condition are superior to those estimated by the CKF estimator. Although the estimation accuracy under low adhesion coefficient conditions is lower than that under high adhesion coefficient conditions, the overall estimation effect is stable, and the error is within a controllable range. At the same time, singular value decomposition can be used to solve least squares problems and principal component analysis as well as matrix compression and denoising applications. Cholesky decomposition is mainly used to solve linear systems of equations and calculate determinants, inverse matrices, etc. of matrices. At the same time, singular value decomposition is robust to small changes in the matrix, and even with small perturbations in the matrix. The changes in singular values are not too significant, which makes it perform better when dealing with noisy data.
Fig. 3Simulation results under the condition of μ =0.2: a) yaw rate; b) side slip angle; c) longitudinal velocity
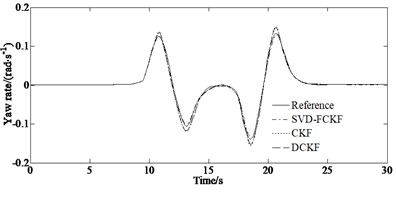
a)
b)
c)
4.2. Experimental verification
A virtual test using the CarSim is conducted to verify the feasibility of the simulated results.
At the same time, this paper conducted real an experimental verification research for a vehicle. The real experimental vehicle is shown in Fig. 4. The measurement devices are shown in Fig. 5.
Fig. 4Real test vehicle


Fig. 5Measurement devices


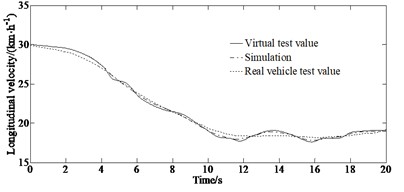
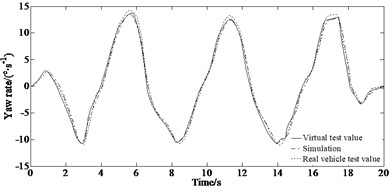
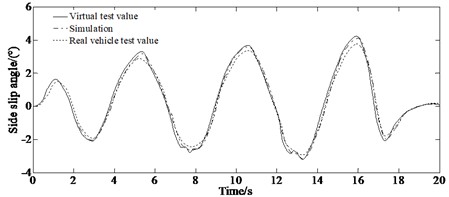
The experimental results of the longitudinal velocity and yaw rate as well as side slip angle of the vehicle under the double lane changing condition are shown in Fig. 6.
Fig. 6Experimental results: a) longitudinal velocity; b) yaw rate; c) side slip angle
a)
b)
c)
The virtual and real vehicle experiment results demonstrate that the algorithm can accurately estimate the vehicle state parameters and has good accuracy. This is because the CKF Kalman filter estimation algorithm is based on the improvement of third-order accuracy, which limits the improvement of its accuracy. It is extended using the fifth-order sphere-radius cubature rule to form the fifth-order CKF. At the same time, in the fifth-order CKF filtering process, more stable singular value decomposition is used instead of Cholesky decomposition, further improving the estimation accuracy and robustness to anomalous observations of the algorithm. It can be seen that there are errors between the test and the simulation value. This is because that the model in the virtual test ignored the nonlinearity of the steering and suspension systems. However, the trend of the virtual vehicle results is consistent with the simulation results, which reflects the virtual situation of the vehicle more realistically verifying the effectiveness of the algorithm.
5. Conclusions
This article applies a SVD-FCKF algorithm estimator to address the issues of low estimation accuracy and poor stability in the process of vehicle state estimation. Based on the third-order CKF, the sphere-radius cubature rule is extended to a fifth-order form, constructing a fifth-order CKF. At the same time, the singular value decomposition is used instead of Cholesky decomposition in covariance matrix decomposition to enhance numerical stability. The effect of the algorithm under high and low adhesion coefficient conditions is simulated and verified. The results show that compared with CKF, the SVD-FCKF estimator has significantly improved the estimation accuracy and stability of the yaw rate and side slip angle as well as longitudinal velocity. It can maintain strong robustness under extreme conditions such as low adhesion coefficient achieving the expected effect and providing reference for active safety research of intelligent vehicles. The virtual experiment results are consistent with the simulation results, so the algorithm can accurately and timely estimate the state parameters. Its accuracy has been verified, and it also provides some theoretical and real vehicle data basis for vehicle stability control.
A higher-degree rule will translate to higher accuracy only if the integrand is well-behaved in the sense of being approximated by a higher-degree polynomial, and the weighting function is known to be a Gaussian density exactly. In practice, these two requirements are hardly met. For example, the integrand function in engineering may not be smooth, or the weight function may be unknown or non-Gaussian. In order to solve the problem, we can adopt an adaptive integration strategy, combining trapz and quad methods for error estimation or dynamically adjust the integration step size instead of relying on fixed high-order rules. And also, we can establish smooth processing for the non-smooth function through convolution operation and construct a smooth function column to approximate the original function or establish different order quadrature rules. In the future, how to solve the above issue should be studied.
References
-
Y. Liu, D. Cui, and W. Peng, “Optimum control for path tracking problem of vehicle handling inverse dynamics,” Sensors, Vol. 23, No. 15, p. 6673, Jul. 2023, https://doi.org/10.3390/s23156673
-
Y. Liu, D. Cui, and W. Peng, “Optimal lane changing problem of vehicle handling inverse dynamics based on mesh refinement method,” IEEE Access, Vol. 11, pp. 115617–115626, Jan. 2023, https://doi.org/10.1109/access.2023.3324422
-
Y. Liu and D. Cui, “Vehicle dynamics prediction via adaptive robust unscented particle filter,” Advances in Mechanical Engineering, Vol. 15, No. 5, p. 168781322311707, May 2023, https://doi.org/10.1177/16878132231170766
-
I. Arasaratnam and S. Haykin, “Cubature Kalman filters,” IEEE Transactions on Automatic Control, Vol. 54, No. 6, pp. 1254–1269, Jun. 2009, https://doi.org/10.1109/tac.2009.2019800
-
K. Shu et al., “Autonomous driving at intersections: A behavior-oriented critical-turning-point approach for decision making,” IEEE/ASME Transactions on Mechatronics, Vol. 27, No. 1, pp. 234–244, Feb. 2022, https://doi.org/10.1109/tmech.2021.3061772
-
H. Wei, H. Zhang, K. Ai-Haddad, and Y. Shi, “Ensuring secure platooning of constrained intelligent and connected vehicles against Byzantine attacks: A distributed MPC framework,” Engineering, Vol. 33, pp. 35–46, Feb. 2024, https://doi.org/10.1016/j.eng.2023.10.007
-
Y. Wang, H. Wei, L. Yang, B. Hu, and C. Lv, “A review of dynamic state estimation for the neighborhood system of connected vehicles,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 7, No. 3, pp. 367–385, Jul. 2023, https://doi.org/10.4271/10-07-03-0023
-
X. He, H. Chen, and C. Lv, “Robust multiagent reinforcement learning toward coordinated decision-making of automated vehicles,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 7, No. 4, pp. 475–488, Sep. 2023, https://doi.org/10.4271/10-07-04-0031
-
G. Hu, W. Wang, Y. Zhong, B. Gao, and C. Gu, “A new direct filtering approach to INS/GNSS integration,” Aerospace Science and Technology, Vol. 77, pp. 755–764, Jun. 2018, https://doi.org/10.1016/j.ast.2018.03.040
-
X. Dong, G. Hu, B. Gao, Y. Zhong, and W. Ruan, “Windowing-based factor graph optimization with anomaly detection using Mahalanobis distance for underwater INS/DVL/USBL integration,” IEEE Transactions on Instrumentation and Measurement, Vol. 73, pp. 1–13, Jan. 2024, https://doi.org/10.1109/tim.2024.3353286
-
G. Hu, L. Xu, B. Gao, L. Chang, and Y. Zhong, “Robust unscented Kalman filter-based decentralized multisensor information fusion for INS/GNSS/CNS integration in hypersonic vehicle navigation,” IEEE Transactions on Instrumentation and Measurement, Vol. 72, pp. 1–11, Jan. 2023, https://doi.org/10.1109/tim.2023.3281565
-
G.-G. Hu, S.-S. Gao, Y.-M. Zhong, and B.-B. Gao, “Stochastic stability of the derivative unscented Kalman filter,” Chinese Physics B, Vol. 24, No. 7, p. 070202, Jul. 2015, https://doi.org/10.1088/1674-1056/24/7/070202
-
G. Hu, B. Gao, Y. Zhong, L. Ni, and C. Gu, “Robust unscented Kalman filtering with measurement error detection for tightly coupled INS/GNSS integration in hypersonic vehicle navigation,” IEEE Access, Vol. 7, pp. 151409–151421, Jan. 2019, https://doi.org/10.1109/access.2019.2948317
-
G. Hu, S. Gao, Y. Zhong, B. Gao, and A. Subic, “Modified strong tracking unscented Kalman filter for nonlinear state estimation with process model uncertainty,” International Journal of Adaptive Control and Signal Processing, Vol. 29, No. 12, pp. 1561–1577, May 2015, https://doi.org/10.1002/acs.2572
-
W. Li, L. Chen, J. Fu, L. Luo, and M. Yu, “State estimation of magnetorheological suspension of all-terrain vehicle based on a novel adaptive Sage-Husa Kalman filtering,” Smart Materials and Structures, Vol. 34, No. 1, p. 015005, Jan. 2025, https://doi.org/10.1088/1361-665x/ad9441
-
S. Goblirsch, M. Weinmann, and J. Betz, “Three-dimensional vehicle dynamics state estimation for high-speed race cars under varying signal quality,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 3371–3378, Oct. 2024, https://doi.org/10.1109/iros58592.2024.10802776
-
Z. Wang, C. Chen, Q. Jiang, H. Zheng, and C. Kaku, “State estimation of drive-by-wire chassis vehicle based on dual Unscented Particle filter algorithm,” Chinese Journal of Mechanical Engineering, Vol. 37, No. 11, pp. 1–15, Feb. 2022, https://doi.org/10.21203/rs.3.rs-1279402/v1
-
X. Li and M. Ren, “Road adhesion coefficient estimation: physics-informed deep learning method with vehicle dynamics model,” Expert Systems with Applications, Vol. 260, p. 125387, Jan. 2025, https://doi.org/10.1016/j.eswa.2024.125387
-
Y. J. Ji, Y. P. Huang, and J. W. Zeng, “A physical-data-driven combined strategy for load identification of tire type rail transit vehicle,” Reliability Engineering and System Safety, Vol. 253, 2025.
-
D. Liu, J. S. Giraldo, P. Palensky, and P. P. Vergara, “Topology identification and parameters estimation of LV distribution networks using open GIS data,” Electrical Power and Energy Systems, Vol. 164, Jan. 2023, https://doi.org/10.2139/ssrn.4661179
-
P. Dahal, S. Mentasti, L. Paparusso, S. Arrigoni, and F. Braghin, “RobustStateNet: robust ego vehicle state estimation for autonomous driving,” Robotics and Autonomous Systems, Vol. 172, p. 104585, Feb. 2024, https://doi.org/10.1016/j.robot.2023.104585
-
G. Hu, L. Xu, Z. Yang, B. Gao, and Y. Zhong, “Indirect fuzzy robust cubature-Kalman filter with normalized input parameters,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 60, No. 5, pp. 5880–5890, Oct. 2024, https://doi.org/10.1109/taes.2024.3397245
-
B. Gao, G. Hu, Y. Zhong, and X. Zhu, “Cubature Kalman filter with both adaptability and robustness for tightly-coupled GNSS/INS integration,” IEEE Sensors Journal, Vol. 21, No. 13, pp. 14997–15011, Jul. 2021, https://doi.org/10.1109/jsen.2021.3073963
-
B. Gao, W. Li, G. Hu, Y. Zhong, and X. Zhu, “Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism for hypersonic vehicle INS/CNS autonomous integration,” Chinese Journal of Aeronautics, Vol. 35, No. 5, pp. 114–128, May 2022, https://doi.org/10.1016/j.cja.2021.08.035
-
B. Gao, G. Hu, L. Zhang, Y. Zhong, and X. Zhu, “Cubature Kalman filter with closed-loop covariance feedback control for integrated INS/GNSS navigation,” Chinese Journal of Aeronautics, Vol. 36, No. 5, pp. 363–376, May 2023, https://doi.org/10.1016/j.cja.2022.12.008
-
B. Gao, G. Hu, Y. Zhong, and X. Zhu, “Cubature rule-based distributed optimal fusion with identification and prediction of kinematic model error for integrated UAV navigation,” Aerospace Science and Technology, Vol. 109, p. 106447, Feb. 2021, https://doi.org/10.1016/j.ast.2020.106447
-
W. Z. Zhao, H. Zhang, and C. Y. Wang, “Estimation of vehicle state parameters based on unscented Kalman filtering,” Journal of South China University of Technology, Vol. 44, No. 3, pp. 76–81, Mar. 2016.
-
S. Lu, M. J. Lian, and Y. Liu, “Comparison of vehicle state estimation based on nonlinear observer and unscented Kalman filter,” Journal of Jilin University (Engineering and Technology Edition), Vol. 50, No. 4, pp. 1288–1300, 2020.
-
S. J. Pan, H. Li, and J. S. Li, “Estimation of side-slip angle of vehicle centroid based on unscented Kalman filter,” Journal of Military Transportation University, Vol. 22, No. 2, pp. 40–45, 2020.
-
K. Jia, Y. F. Pei, and Z. H. Gao, “A quaternion-based robust adaptive spherical simplex Unscented Particle filter for MINS/VNS/GNS integrated navigation system,” Mathematical Problems in Engineering, Vol. 2019, pp. 1–12, 2019.
-
Z. Gao, D. Mu, Y. Zhong, and C. Gu, “Constrained unscented particle filter for SINS/GNSS/ADS integrated airship navigation in the presence of wind field disturbance,” Sensors, Vol. 19, No. 3, p. 471, Jan. 2019, https://doi.org/10.3390/s19030471
-
W. Wei, S. Gao, Y. Zhong, C. Gu, and G. Hu, “Adaptive square-root unscented Particle filtering algorithm for dynamic navigation,” Sensors, Vol. 18, No. 7, p. 2337, Jul. 2018, https://doi.org/10.3390/s18072337
-
Y. Liu, D. Cui, and W. Peng, “Vehicle state and parameter estimation based on improved extend Kalman filter,” Journal of Measurements in Engineering, Vol. 11, No. 4, pp. 496–508, Dec. 2023, https://doi.org/10.21595/jme.2023.23475
-
W. B. Wu et al., “Singular value decomposition fifth-order cubature Kalman filter for vehicle state estimation,” Journal of Chongqing University of Technology, Vol. 38, No. 3, pp. 74–83, 2024.
About this article
This research was supported by the Open Research Program of Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing under Grant No. UMPIC202404.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Yingjie Liu: mathematical model and simulation techniques. Chenglian Xie: virtual validation.
The authors declare that they have no conflict of interest.
