Machining parameters optimization in high-speed milling of titanium alloy chips

1. Introduction

With the rapid development of computer technology, the finite-element numerical simulation method has gained growing popularity in the research on the cutting – process mechanisms of titanium alloys and other metals. This method enables the analysis of various aspects, including chip formation, tool behavior, and the distribution of temperature fields, stress fields, strains, and strain rates within the workpiece. Through subsequent calculation and analysis, optimal processing parameter designs can be obtained. This not only helps reduce costs in the actual machining process but also optimizes machining designs and processes.

A novel approach for machining parameter optimization is presented through the integration of the cutting process with finite element analysis. Laakso et al. [1] used the finite element simulation method to estimate the influence of the subsequent cutting process on the performance of the cutting model, and found the error of the feed force. Li et al. [2] studied the chip formation mechanism of high-temperature nickel alloy Inconel 718 in the cutting process by combining design milling experiment and finite element simulation, established a two-dimensional cutting model based on J-C constitutive model [3], and found that the cutting force and chip morphology generated by finite element simulation were basically consistent with the experiment. Walid Jomaa et al. [4] used Abaqus/Explicit v6.13 software to simulate AA7075-T651 alloy with two-dimensional finite element processing. By using finite element numerical data and chip sawtooth analysis model, the physical phenomenon controlling sawtooth chip formation was emphasized and discussed in depth.Rodriguez Prieto et al. [5] conducted an investigation on the cutting of Ti6Al4V. They modified the Lagrangian finite - element method by basing it on the particle finite-element method and continuous Delaunay re-triangulation. Arrazola et al. [6] established a two-dimensional finite-element model by employing the arbitrary Lagrange-Euler formula available in Abaqus/Explicit (v6.8). They discovered that thermal conductivity, specific heat, inelastic percentage, and the Johnson-Cook (J-C) constitutive coefficients have significant impacts on the formation of saw-tooth chips. In particular, thermal conductivity and specific heat exert the most substantial influence. In addition, it is found that the yield stress of the material itself has a significant effect on the generation of sawtooth chips. Huang et al. [7] proposed a new Galerkin grid-free method when studying the chip separation process in the machining process, and proved that the formation of shear bands was caused by the thermal softening of materials.

Sima et al. [8] explored the influence of a modified material model, which was based on temperature-dependent flow softening, on the formation of saw-tooth chips during the machining of Ti-6Al-4V titanium alloy. The research revealed that the flow-softening phenomenon, strain-hardening effect, and thermal-softening effect are all interrelated. Fu et al. [9] studied the chip morphology changes of 7050-T7451 aluminum alloy at different cutting speeds by using the finite element simulation method, and found that continuous chips were more easily formed when the cutting speed was lower than 1500 m/min, and when the critical cutting speed was reached (2500 m/min), the ribbon chips were transformed into sawn-shaped chips. Rhim et al. [10] studied the flow stress model based on the assumption of high speed, high temperature and large deformation process to predict the formation of sawtooth chips during cutting. The finite element analysis shows that the dynamic recrystallization will be induced by the increase of shear zone temperature during the cutting process, the flow stress will be reduced, and the adiabatic shear zone and sawtooth chip will be formed.

In complex processing, due to numerous influencing factors, it is not easy to establish a theoretical model, while the data-driven model that relies on test data is relatively easy to obtain, and there is no need to analyze the construction mechanism of the objective function. Data modeling is an important means to optimize machine tool efficiency and processing efficiency, and commonly used methods include response surface method [11], inverse propagation neural network (BPNN) [12], support vector regression and progressive gradient regression tree. Response surface method [13] reveals the correlation between decision variables and target variables by constructing a quadratic polynomial model. However, when there are items with insignificant influence, it is necessary to artificially eliminate them to improve the prediction accuracy, which may be time-consuming and difficult to obtain the best results. In contrast, the other three methods can improve the accuracy of the model by adjusting the internal parameters, especially for nonlinear data. When selecting the data modeling method, it is necessary to consider the complexity of the model, the difficulty of parameter adjustment and the fitting ability of nonlinear data according to the specific situation, so as to achieve the best modeling effect. Yunchao Tang et al. [14] trained a Support Vector Regression (SVR) model using data from 120 sets of UCS and peak strain experiments, constructing a multi-objective optimization model based on SVR. They successfully generated a Pareto front for mixed optimization design across three objectives (UCS, strain, cost), serving as a decision reference under different temperature conditions. Shuai Wan et al. [15] proposed an ultrasonic-AI hybrid method, enhancing the Extreme Gradient Boosting (XGBoost) model through over-sampling and hyperparameter optimization via Bayesian Optimization (BO-XGBoost). The BO-XGBoost model demonstrated outstanding performance, with an overall prediction accuracy of 0.92, an accuracy and recall rate of 0.90, and an AUC of 0.98.

In addition, the selection of optimization targets is also very important. Tamal Ghosh et al. [16] uses Bayesian regularization neural network and beetle antenna search algorithm for process optimization. By applying Kohonen’s self-organization diagram, the relationship between different processing parameters is explored. After conducting a comparative analysis of the proposed agent-assisted optimization method with three other optimization techniques, it was found that the former demonstrated remarkable efficiency and rapidity in handling offline processing data. The findings of this study clearly indicate that the agent-assisted optimization method achieved success in the optimization process and exhibited significant advantages over its counterparts.

Previous studies have mostly focused on the formation of chip material or analysis of machining parameters, lacking innovation in the application of parameter optimization algorithms. This study makes breakthroughs in three aspects: First, addressing the issue of unclear mechanisms for selecting machining parameters influenced by chip morphology during high-speed cutting of titanium alloys, we systematically simulated Ti6Al4V chip morphology under different speeds and temperatures, conducting an in-depth analysis of the formation processes and mechanisms of straight-cut and serrated chips, filling a research gap in this field; Second, innovatively employing the ant colony optimization algorithm for multi-objective parameter optimization, which offers significant advantages over traditional genetic algorithms and particle swarm optimization in balancing global and local search, flexibility in parameter adjustment, and structural innovation, proposing high-performance machining through high feed rates, radial cutting depth, and spindle speed, providing new insights for parameter selection; Third, deeply integrating the cutting process with finite element analysis to form a novel method for optimizing machining parameters, offering more scientific and systematic solutions to improve the quality of high-speed milling of titanium alloys, promoting the development of titanium alloy machining technology.

In this paper, ABAQUS software based on ALE Arbitrary Lagrangian Eulerian is used. The method combines the advantages of Lagrangian and Eulerian algorithm [17], and can be used to simulate large deformation and steady deformation path of materials. The problems of mesh redivision and cutting separation are solved. Nevertheless, we still need to face the challenges of optimization of titanium alloy machining parameters, especially in the field of multi-objective optimization. In order to overcome these problems, we are committed to building a cutting parameter optimization model and method for titanium alloy milling, and combining it with the process database.

2. Finite element simulation research based on ABAQUS

This study utilized ABAQUS finite element simulation analysis software to establish a simulation model. By systematically varying the cutting parameters and analyzing the relevant variables, the model employed a modified Johnson-Cook nonlinear thermovisco-plastic constitutive model, a shear failure chip fracture criterion, and a bond slip mixed friction model. These enabled the acquisition of chip morphologies at different cutting speeds.

2.1. Research on chip morphology at different cutting speeds

1) In order to study the shape of chips at different cutting speeds, the initial temperature of the tool is set at 20 ℃, the ambient temperature is 20 ℃, and the cutting depth is 0.1 mm. The tool material is assumed to be rigid body, sharp and have no tool wear, and its model is 4.61 mm long, 2.56 mm wide, front corner 0 and rear corner 10. The workpiece model is 15 mm long and 8 mm wide.

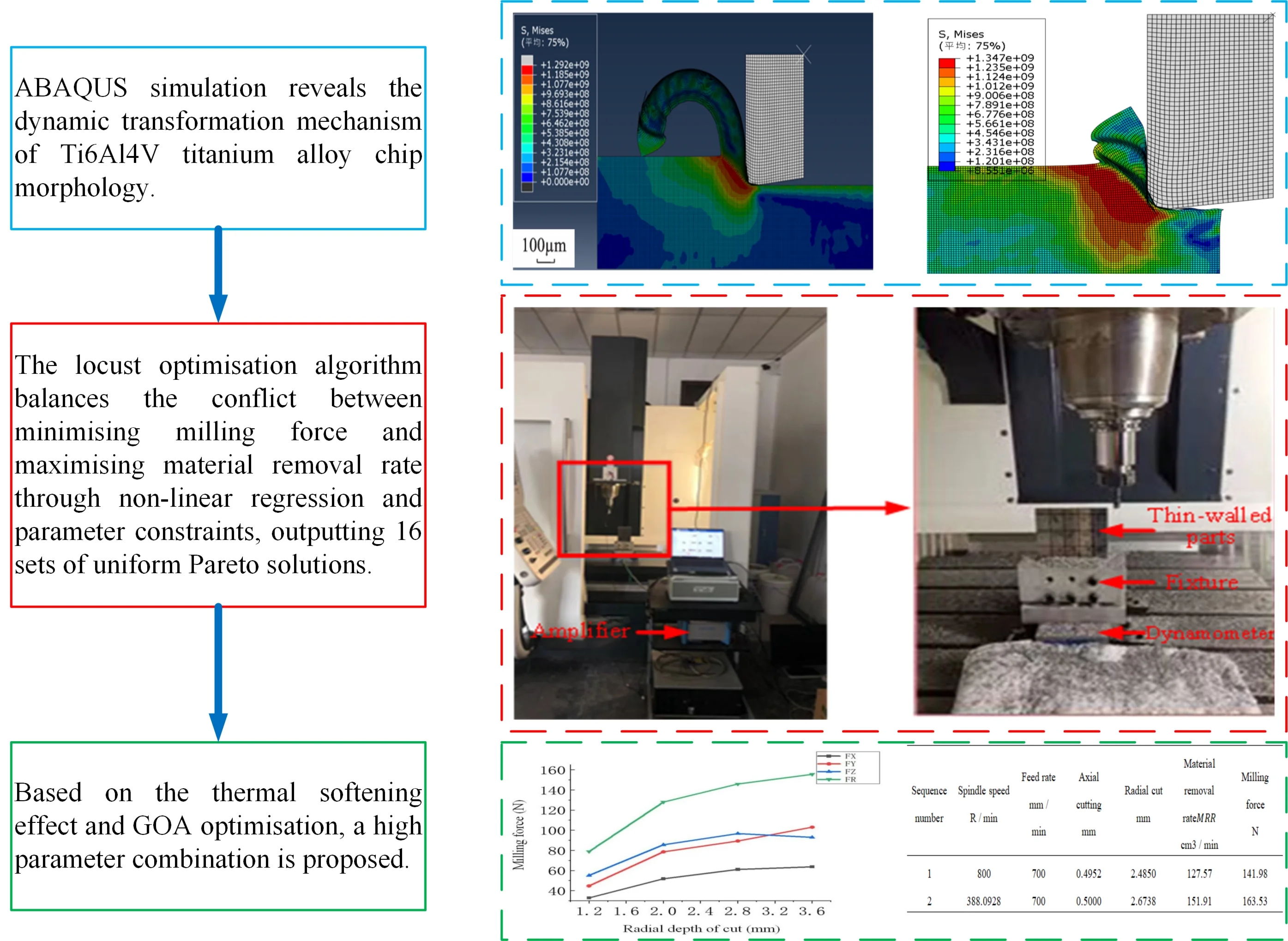
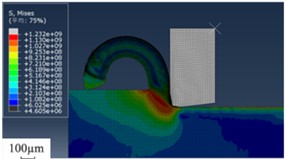
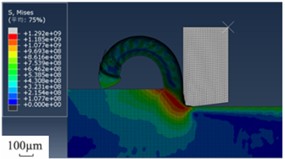
In the high speed machining of titanium alloy chips, the chip type changes with the processing speed, and its conversion mechanism is mainly affected by the interaction of strain hardening and thermal softening. The stress distribution is shown in the figure below. From the chip morphology in Fig. 1, it can be seen that a continuous ribbon chip is obtained at a low processing speed of 0.5 m/s. At this time, the heat generated in the cutting process is relatively small, and the strain hardening effect of the material occupies the dominant position, which can resist the deformation caused by the cutting, so that the chip can be formed continuously and maintain the belt shape. When the cutting rate increases to 1.5 m/s, the generated chips gradually have a sawtooth shape, and the left half has an uneven wavy profile, but the sawtooth shape is not significant at this time, and it should be a transitional form of banded chips and sawtooth chips. At this time, there is no abrupt transition to shear instability because the strain-hardening effect prevails over the heat-softening effect. When the cutting speed was increased to 2.0 m/s, a saw-tooth chip segment formed with a significant saw-tooth degree, yet no characteristics of adiabatic shear bands were observed. The antagonism between strain hardening effect and thermal softening effect makes the chip present a more regular sawtooth shape. When the cutting speed is increased to 7.5 m/s, a relatively regular sawtooth chip has been formed, the degree of sawtooth has been very high, sudden shear instability appears, and an obvious adiabatic shear zone has been formed. This is because at this time, the cutting speed is greatly increased, and a large amount of heat is generated in the cutting area. The thermal softening effect exceeds the strain hardening effect, and the material is rapidly softened locally, resulting in shear instability and forming an adiabatic shear band, and the chip presents a typical sawtooth shape.

Fig. 1Chip morphology stress (N) cloud diagram at different speeds (m/s)

a)$v=$0.5 m/s

b)$v=$1.0 m/s

c)$v=$1.5 m/s

d)$v=$2.0 m/s

e)$v=$7.5 m/s

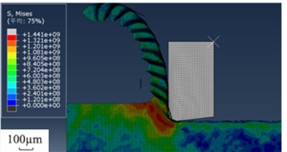
f)$v=$12.5 m/s

2) The specific formation process of sawtooth nodal block at the same speed.

In this model, the joint temperature, stress field, equivalent plastic strain and milling force of titanium alloy during sawing process were simulated by using the finite element numerical analysis method. As shown in Fig. 2-3, the zigzag chip break is clearly shown, and the selected tool front Angle is 0° and the cutting speed is $v=$7.5 m/s.

As shown in Fig. 2, the chip layer material connected to the previous segment of sawtooth chips has an uneven temperature distribution, and there is a significant temperature rise at the cutting edge of the tool. This is mainly because the heat dissipation of the cutting layer is the worst closest to the cutting edge of the tool, and the shear-sliding from the previous step affects a limited area of the chip. Due to the rolling action of the tool and the increase in temperature, the material near the cutting-edge area undergoes high-degree shear-sliding deformation. Finally, due to the extrusion of the tool with the resulting chips, as shown in Fig. 2(b), the Mises stress generated at this time was large and extended to the inside of the workpiece, which had an impact on the surface quality of the workpiece.

As shown in Fig. 3, during the cutting process of titanium alloy simulated by finite element simulation, due to the metal material being located in a critical thermoplastic instability condition, strong shear slip was generated in the entire shear slip narrow band, resulting in a zigzag shape at the top of the chip. Correspondingly, the temperature in the central region of the narrow deformation band continued to rise, and all the metals in the narrow band showed thermoplastic instability, up to 4.05, and the Mises stress decreased, as shown in Fig. 3(b). With the continuous cutting process, the sawtooth deposit body continues to undergo concentrated shear-slip deformation, and the sawtooth structure on the top of the sawtooth deposit body will also increase, and finally form a sawtooth deposit body.

Fig. 2The third section serrated chip formation began to form

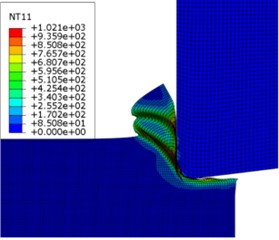
a) Node temperature distribution cloud map

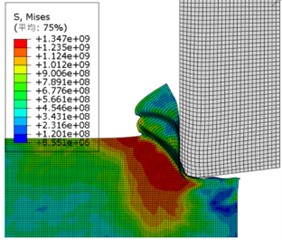
b) Stress distribution cloud map

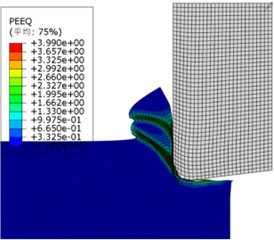
c) Equivalent plastic strain distribution cloud map

d) Cutting force distribution cloud map

Based on the analysis, the force applied by the tool to the workpiece, which is closely related to the formation mechanism of saw-tooth chips, is the primary factor leading to the elastic deformation of the workpiece and the cutting layer. In detail, during the cutting operation, the material at the tool tip experiences plastic deformation as a result of the synergistic influences of temperature, stress, strain, and other relevant factors.

A substantial amount of heat is generated during the cutting process due to the plastic deformation of the material and frictional work, which leads to the thermal softening of the material. During the shearing process, the reduction in shear stress caused by thermal softening is greater than the increase in stress resulting from machining-induced strengthening, which leads to the generation of shear fold and the first deformation zone is formed quickly in the cutting layer. In this process, chips begin to slide and accumulate on the processed material, finally forming a zigzag chip. Finally, a new “zigzag” chip breaking mechanism is obtained under the cutting process.

2.2. ABAQUS 3D milling simulation

The finite element model of 3D milling is shown in Fig. 4. A YG6X flat-head end mill is selected with 4 blade numbers, 45° spiral Angle, 7° front edge Angle, 15° back edge Angle, and 5 diameter. The workpiece material is Ti6Al4V. The axial cutting depth is 3 mm and the radial cutting depth is 4.5 mm. The initial temperature is 30 ℃, the bottom surface of the workpiece is constrained by 6 degrees of freedom, and the rigid constraint of the milling cutter is set as a reference point. Subsequently, the degrees of freedom of rotation and movement are applied to the reference point to establish a dynamic thermodynamic coupling analysis step. Finally, ABAQUS/Explicit solver is used for calculation.

Fig. 3The third serrated chip shear slip occurs and completely formed

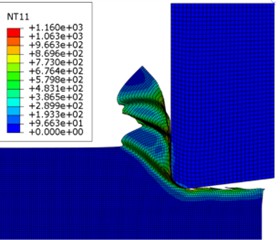
a) Node temperature distribution cloud map

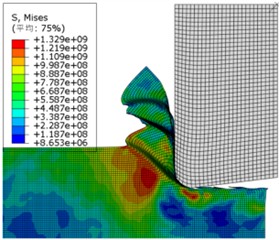
b) Stress distribution cloud map

c) Equivalent plastic strain distribution cloud map

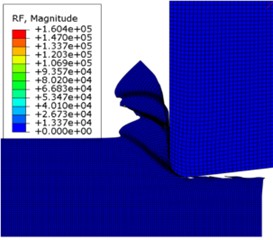
d) Cutting force distribution cloud map

In the process of 3D milling, when the temperature change of a certain point of the workpiece is wanted to be studied, the temperature change of points under the same $X$ coordinate and different $Z$ coordinate can be selected as shown in Fig. 4(b), and the distance between the unit node and the machining surface can be 0 mm, 0.7 mm, 1.4 mm and 2.1 mm respectively. The temperature measurement points we selected can cover different depth levels: points at distances of 0 mm, 0.7 mm, 1.4 mm and 2.1 mm from the machining surface. These points at different distances span from the machining surface to various depths within the workpiece, allowing for a comprehensive examination of the heat conduction and distribution of milling thermal effects in the thickness direction of the workpiece. The machining surface (0 mm) directly participates in the cutting process, with intense temperature changes; as the distance increases, the temperature decay and variation characteristics during heat conduction into the workpiece can be observed. Additionally, temperature responses can be compared: by outputting and plotting the temperature changes at these different depth points, it is clear that as the normal distance (distance from the machining surface) increases, the peak temperature of the measurement point decreases and the time to reach the peak temperature becomes longer, indicating a temperature response lag. This comparison provides effective data support for understanding the propagation mechanism of milling thermal effects within the workpiece and the thermal influence range, thereby providing a basis for optimizing milling process parameters and controlling thermal deformation of the workpiece.

Fig. 5 shows the output and simultaneous plotting of the temperature variations of the four cell nodes. As the normal range increases, the peak temperature at the measuring point decreases. Meanwhile, it takes each measuring point a longer time to reach the peak temperature. In other words, the temperature response of the measuring point lags to some extent as the normal stroke increases.

Fig. 43D milling model

a) Three-dimensional milling model

b) Schematic diagram of unit node selection

Fig. 5The change of element node temperature with time

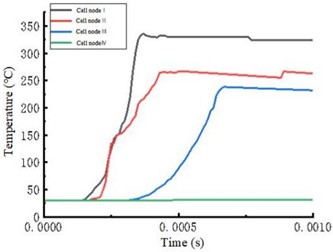
Fig. 6Experimental platform

As the position of the unit node moves down, the temperature of the area between the adjacent sawtooth is getting higher and higher, and the edge of the sawtooth shows the characteristics of melting metal, at the same time, in the case of no change in heat dissipation capacity, the cutting heat per unit time is increased, thereby increasing the cutting temperature, and then strengthening the thermal softening effect, so that the strength and hardness of titanium alloy in the deformation area are reduced. As the degree of material deformation increases, the degree of chip serration increases. At this time, when an external load is applied to the area, cracks appear between the adjacent sawtooth, causing the sawtooth to separate [18].

3. Experimental platform construction

The cutting force in milling process is directly related to milling efficiency, heat production, tool loss, workpiece vibration and surface quality. This parameter provides a crucial theoretical basis and evaluation criterion for the design and operation of machine tools, cutting tools, and fixtures. Moreover, the effects of various processing factors on cutting force differ. At the same time, by observing the dynamic cutting force of the tool, we can effectively evaluate the wear of the tool and the vibration of the system during the milling process. In the process of cutting titanium alloy, the chip heterogeneity often leads to high frequency fluctuation of cutting force. After a lot of experiments and in-depth theoretical analysis, we have identified two main sources of cutting force in the cutting process: first, the elastoplastic deformation of cutting layer metal, chip and workpiece surface metal; Secondly, the friction between the chip and the workpiece during the cutting process is also an important source of cutting force.

Aiming to accurately predict the cutting force under diverse process conditions and provide a basis for the rational selection of milling parameters, this research endeavors to develop the relevant theoretical model by studying the variation law of cutting force. For Ti6Al4V titanium alloys, the processing speed is greater than 100 m/min, which is considered as high-speed milling. In this study, 16 four-factor and four-level orthogonal tests are proposed to obtain milling force as the goal, and orthogonal tests with 4 factors and 4 levels are adopted to determine the levels of each factor as shown in Table 1 and milling process parameters as shown in Table 2. The DMC635V vertical CNC machining center produced by De Magee was used in the test. The relevant parameters are as follows: the positioning accuracy is 0.008 mm, the repeated positioning accuracy is 0.005mm. The spindle conical hole is SK40, the standard spindle speed can reach 8000rpm, the feed speed is 20 m/min, and the fast moving speed can reach 30 m/min. Under the control of Siemens system, it has four machining axes, $X$, $Y$, $Z$ and rotation axis, which ensures accurate positioning and stable processing, ensuring the accuracy of the test. Fig. 6 shows the design of this test bed.

In this experiment, Xiamen Jinlu brand coated four-sided milling cutter with diameter of 10 mm and screw Angle of 45 degrees was used. This test takes Ti6Al4V titanium alloy as the research object and connects it with the force measuring instrument Kistler9257B. Kistler9257B is an advanced dynamometer that can simultaneously measure milling forces and moments in $X$, $Y$ and $Z$ directions. The system also includes a charge amplifier and related wire device.

To minimize the impact of burrs on the test results, prior to the commencement of the machining test, a large radial cutting depth was initially employed to remove burrs. Subsequently, to further reduce the effect of minor surface irregularities of the workpiece on the milling force, a one-time milling approach with zero radial cutting depth was adopted.

Dyno Ware software was used to derive the cutting force data from the signal measured by the dynamometer. Taking the cutting parameters ($f_d=$200 m/min, $a_p=$0.1 mm, $n_s=$1900 r/min, $a_r=$5 mm) as an example, through the analysis of the cutting component forces $F_X$, $F_Y$ and $F_Z$, it was obtained that in the steady state machining process, the cutting force of the machine would be reduced. The relationship between cutting force and time per milling cutter rotation curve 7.

The cutting force generated during the milling process of the workpiece by the tool varies with the movement of the tool’s four teeth. This is because the engagement and disengagement of the tool teeth with the workpiece during the milling operation have a significant impact on the cutting force. At the beginning of the machining process, the cutting force gradually increases from the minimum to the maximum. Subsequently, during the ongoing machining, the cutting force gradually decreases.

Fig. 7Cutting force periodic signal diagram

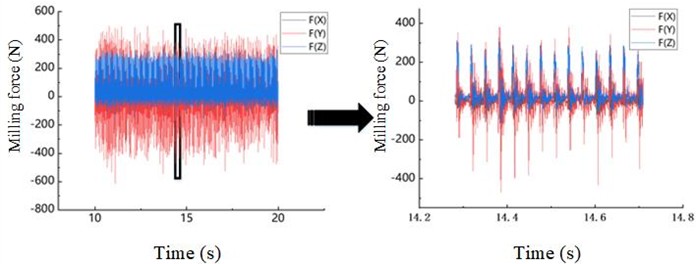
Fig. 8Relationship between four feed speed and milling force

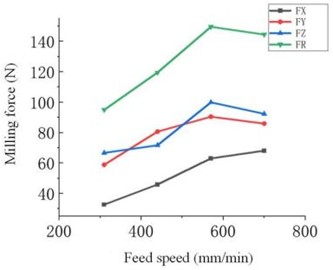
Fig. 8 shows the law of influence of horizontal changes of milling parameters on milling force, where FX, FY and FZ are the average $X$, $Y$ and $Z$ direction milling force measured by the force meter respectively, and FR is the maximum value of the milling force.

It can be seen from Fig. 8 that with the increase of feed speed, the milling force in $X$, $Y$, $Z$ direction and in the direction of milling force is on the rise, but it turns downward at 570 mm/min. According to Schulz and Senzovsky [19], increasing the milling speed during the operation accelerates the plastic strain rate of the material, leading to strain-rate hardening. Consequently, the milling force increases. Due to the limited thermal conductivity of titanium-alloy materials, a higher milling speed results in more significant temperature rises. As the thermal-softening effect of the material gradually overtakes and dominates the strain-rate hardening effect, both the hardness and strength of the material, as well as the milling force, decrease. The results show that the thickness and milling force of undeformed chips and the degree of sawtooth serration increase with the increase of feed speed and cutter quantity per tooth [20].

4. Optimization of processing parameters based on chip morphology

4.2. Optimization of processing parameters based on locust optimization algorithm

4.2.1. Parameter constraints and determination of multi-objective optimization model

When solving the optimization model of milling processing parameters, the processing parameters need to be constrained. According to the actual processing situation and machine tool performance, the constraint range of cutting parameters is:

14

$\left\{\begin{array}{l}200\le n\le 800,\\ 0.2\le a_p\le 0.5,\\ 310\le V_f\le 700,\\ {1.2\le a}_r\le 3.6.\end{array}\right.$

Therefore, the multi-objective optimization model can be obtained as follows:

15

$\left\{\begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}{F}_R\left(n,a_p,V_f,a_r\right),\\ \max MRR\left(a_p,V_f,a_r\right),\\ 200\le n\le 800,\\ 0.2\le a_p\le 0.5,\\ 310\le V_f\le 700,\\ {1.2\le a}_r\le 3.6.\end{array}\right.$

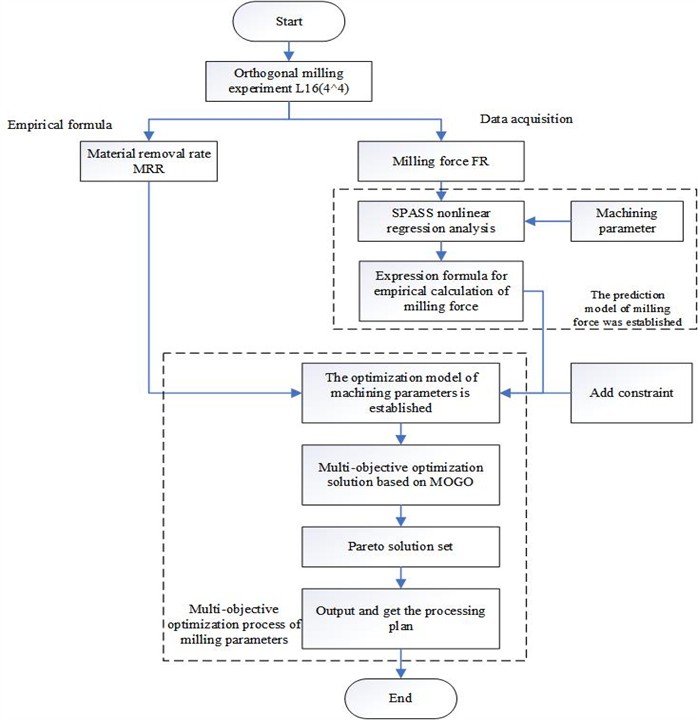
In order to obtain the Pareto solution of the multi-objective optimization model [24], the following solution flow Fig. 9 is given. As illustrated in the figure, the milling force and resultant force data were acquired through meticulously designed milling experiments. Meanwhile, the material removal rate was calculated using a specific formula. Subsequently, SPSS software was employed to conduct nonlinear regression analysis for prediction purposes, thereby establishing a relationship model between the cutting force and cutting parameters. A multi-objective optimization model of cutting parameters was established to minimize the resultant cutting force and maximize the material removal rate, and was optimized by MOGOA algorithm. Finally, the solution is obtained from Pareto frontier.

4.2.2. Optimization results and analysis

The multi-objective optimization model was solved based on the locust optimization algorithm. Parameters were set as follows: the population number was 200 and the number of iterations was 100. After multiple iterations of the optimization algorithm, the optimization results were obtained, as shown in Fig. 10.

Fig. 9Flow chart of process parameter optimization solution

As depicted in Fig. 10, the optimization results of the two objective functions, namely the maximum material removal rate and the minimum milling force, are in conflict with each other. Specifically, the milling force increases as the material removal rate rises. When the milling force is low, the material removal rate is also low. When selecting machining parameters, the requirements of the actual manufacturing process should be considered. The multi-objective parameter optimization provides a basis for the selection of cutting parameters. Table 7 presents the 16 groups of Pareto-optimal solutions generated based on the multi-objective optimization results.

Through in-depth analysis of the proposed optimization results, it is obvious that the optimal solution shows a tendency of uniform distribution along the Pareto optimal solution in the two key objective functions of milling force and material removal rate. This distribution pattern demonstrates excellent performance and accuracy in finding the best solution.

In order to verify the effect of optimization of machining parameters, two groups of optimization parameters are carefully selected from 16 groups of Pareto optimal solution sets and verified by experiments. Since the material removal rate can be calculated directly by the formula, we focus on the measurement experiment of milling force. The comparison between experimental results and optimization parameters is shown in Table 8, which provides a basis for us to evaluate the rationality of optimization results. According to Table 8, the errors of the optimized milling force value and the experimental milling force value are 11.3 % and 7.65 % respectively, which is within the allowable range, proving the rationality of the optimization results. In the mechanical processing industry, there is no absolute unified standard for the error range between the predicted value and the experimental value of milling force. In the rough machining of ordinary mechanical manufacturing, the processing accuracy is relatively low and the focus is on improving efficiency. Therefore, the error range of 11.3 % and 7.65 % is acceptable.

Fig. 10Pareto solution set curve

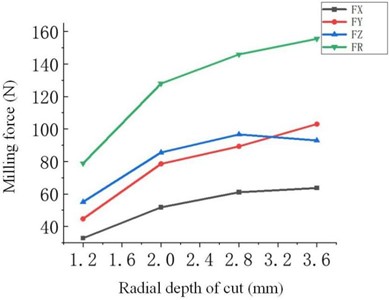
Table 7The trade-offs between milling force (FR) and material removal rate (MRR)

Sequence number	Spindle speed (R/min)	Feed rate (mm/min)	Axial cutting (mm)	Radial cut (mm)	Material removal rate $MRR$ (cm3/min)	Milling force (N)
1	800	700	0.4952	2.4850	861.41	127.57
2	200	700	0.4961	2.4827	862.15	127.59
3	388.0939	700	0.5000	2.5169	880.92	132.36
4	800	700	0.5000	2.5108	878.77	130.64
5	800	700	0.5000	2.5392	888.72	134.06
6	800	700	0.4966	2.4857	864.10	127.65
7	388.0928	700	0.5000	2.6738	935.84	151.91
8	800	700	0.4987	2.4857	867.68	127.66
9	800	700	0.5000	2.5509	892.81	135.48
10	800	700	0.4979	2.4857	866.49	127.65
11	800	700	0.5000	2.5103	878.62	130.59
12	800	700	0.5000	2.6731	935.58	150.77
13	288.2984	700	0.5000	1.7001	595.05	52.07
14	288.2984	700	0.5000	1.7014	595.51	52.17
15	668.4960	700	0.4860	1.3782	468.85	30.92
16	200	700	0.4882	2.0395	696.92	80.41

In order to ensure that the quality of the processed titanium alloy meets the expected standards and meets various processing constraints, a larger feed speed, radial depth of cut and spindle speed are used.

The locust optimization algorithm provides an effective method to optimize the milling process parameters to achieve high performance machining results. This method can not only improve the processing quality, but also reduce the production cost and shorten the time to market. Therefore, in the future engineering applications, this optimization algorithm will be more widely used and recognized.

Table 8Pareto optimal solutions

Sequence number	Spindle speed (R/min)	Feed rate (mm/min)	Axial cutting (mm)	Radial cut (mm)	Material removal rate $MRR$ (cm3/min)	Milling force (N)
1	800	700	0.4952	2.4850	127.57	141.98
2	388.0928	700	0.5000	2.6738	151.91	163.53

5. Conclusions

This paper conducts a finite-element simulation study using ABAQUS, focusing on the simulation and analysis of cutting force, cutting temperature, and chip morphology. Additionally, it delves into the application of multi-objective optimization algorithms for the optimization of cutting process parameters. Based on these investigations, the following conclusions are drawn:

1) Simulation of the cutting process under different cutting speeds shows that the cutting speed increases, the thermal softening effect increases, and the average flow stress decreases, thus reducing the cutting force. By analyzing the process of chip formation, the workpiece material is elastic deformed by cutting tool extrusion, and the cutting layer is formed. As the cutting progresses, the chip gradually takes on a zigzag shape. Through the simulation analysis of temperature variations, it was discovered that the peak temperature at the measuring point significantly increases as the normal measuring distance decreases.

2) Orthogonal experiments are designed to collect milling force data, and several sets of experiments are carried out for different milling parameters. Optimization objective function is determined, milling force regression model and material removal rate regression model are established, parameter constraint and multi-objective optimization are carried out. In actual manufacturing, the material removal speed can be accelerated, the processing time can be reduced, and the production efficiency can be improved. For example, in mass production of parts, the overall processing cycle can be shortened. The multi-objective optimization model is solved by locust optimization algorithm, and 16 Pareto optimal solutions are obtained, which provides an important basis for the selection of cutting parameters in actual machining process.

3) Although FEM has many advantages, it has some limitations. This study is based on the limitations of ABAQUS finite element simulation. First, the constitutive models we use are mostly simplified assumptions, making it difficult to accurately reflect the true mechanical behavior of titanium alloys under complex high-speed cutting conditions. They fail to adequately consider the coupled effects of strain rate and temperature. Second, the parameter schemes obtained from multi-objective optimization are based on specific condition influences, which limit their applicability in diverse industrial production scenarios.